Đề cương ôn tập môn Hình học Lớp 8 - Chương 1

 ĐỀ ễN TẬP HỎA TỐC-CORONA CHƯƠNG I-HèNH HỌC 8
 I. TểM TẮT Lí THUYẾT
 * Ngoài định nghĩa và dấu hiệu nhận biết đó trỡnh bày chi tiết trong từng vấn đề, trong bài ụn tập chương này, tỏc giả túm 
 tắt tớnh chất của từng hỡnh theo cạnh, gúc, đường chộo và tớnh chất đối xứng để giỳp giả sử dụng cỏc tớnh chất của cỏc hỡnh 
 để vận dụng vào giải toỏn một cỏch dễ dàng hơn.
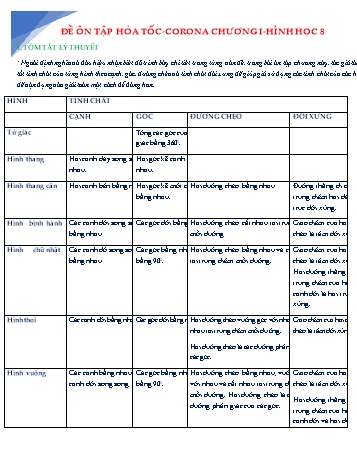
HèNH TÍNH CHẤT
 CẠNH GểC ĐƯỜNG CHẫO ĐỐI XỨNG
Tứ giỏc Tổng cỏc gúc của một tứ 
 giỏc bằng 3600.
Hỡnh thang Hai cạnh đỏy song songHai với gúc kề cạnh bờn bự 
 nhau. nhau.
Hỡnh thang cõn Hai cạnh bờn bằng nhau.Hai gúc kề một đỏyHai đường chộo bằng nhau Đường thẳng đi qua 
 bằng nhau. trung điểm hai đỏy là 
 trục đối xứng.
Hỡnh bỡnh hành Cỏc cạnh đối song songCỏc và gúc đối bằng Hainhau. đường chộo cắt nhau tại trungGiao điểm điểm của hai đường 
 bằng nhau mỗi đường chộo là tõm đối xứng.
Hỡnh chữ nhật Cỏc cạnh đố song songCỏc và gúc bằng nhauHai và đường chộo bằng nhau và cắtGiao nhau điểm của hai đường 
 bằng nhau bằng 900. tại trung điểm mỗi đường. chộo là tõm đối xứng 
 Hai đường thẳng đi qua 
 trung điểm của hai cặp 
 cạnh đối là hai trục đối 
 xứng.
Hỡnh thoi Cỏc cạnh đối bằng nhau.Cỏc gúc đối bằng nhau.Hai đường chộo vuụng gúc với nhauGiao và c đắti ểm của hai đường 
 nhau tại trung điểm mỗi đường. chộo là tõm đối xứng.
 Hai đường chộo là cỏc đường phõn giỏc của 
 cỏc gúc.
Hỡnh vuụng Cỏc cạnh bằng nhau CỏcCỏc gúc bằng nhauHai và đường chộo bằng nhau, vuụngGiao gúc điểm của hai đường 
 cạnh đối song song bằng 900. với nhau và cắt nhau tại trung điểmchộo là tõm đối xứng.
 mỗi đường. Hai đường chộo là cỏc 
 Hai đường thẳng đi qua 
 đường phõn giỏc của cỏc gúc.
 trung điểm của hai cặp 
 cạnh đối và hai đường chộo là bốn trục đối 
 xứng.
II. CÁC ĐỀ ễN HỎA TỐC
ĐỀ 1-Cơ Bản
1A. Cho tam giỏc ABC cõn tại A, trung tuyến AM. Gọi I là trung điểm của AC, K là điểm đối xứng của điểm M 
qua điểm I.
a) Tứ giỏc AMCK là hỡnh gỡ ?
b) Tứ giỏc AKMB là hỡnh gỡ ?
c) Cú trường hợp nào của tam giỏc ABC để tứ giỏc AKMB là hỡnh thoi khụng ? Vỡ sao ?
1B. Cho tam giỏc ABC vuụng tại A, trung tuyến AM. Gọi D là trung điểm của AB, E là điểm đối xứng của điểm 
M qua điểm D.
a) Chứng minh điểm E đối xứng với điểm M qua đường thẳng AB.
b) Cỏc tứ giỏc AEMC, AEBM là hỡnh gỡ ?
c) Cho BC = 4 cm. Tớnh chu vi tứ giỏc AEBM.
d) Tam giỏc vuụng ABC thỏa điều kiện gỡ thỡ AEBM là hỡnh vuụng?
2A. Cho hỡnh vuụng ABCD. E là điểm trờn cạnh DC, F là điểm trờn tia đối của tia BC sao cho BF = DE.
a) Chứng minh tam giỏc AEF vuụng cõn.
b) Gọi I là trung điểm của EF. Chứng minh I thuộc BD.
c) Lấy điểm K đối xứng với A qua I. Chứng minh tứ giỏc AEKF là hỡnh vuụng.
2B. Cho tam giỏc ABC vuụng tại A, đường cao AH, trung tuyến AM.
a) Chứng minh Bã AH Mã AC.
b) Trờn đường trung trực Mx của đoạn thẳng BC, lấy điểm D sao cho MD = MA (D và A thuộc hai nửa mặt phẳng 
đối nhau bờ BC). Chứng minh rằng AD là phõn giỏc chung của Mã AH &Cã AB.
c) Từ D kẻ DE, DF lần lượt vuụng gúc với AB và AC. Tứ giỏc AEDF là hỡnh gỡ ?
d) Chứng minh DBE DCF
3A. Cho hỡnh vuụng ABCD. Gọi E là điểm đối xứng của điểm A qua điểm D. a) Chứng minh tam giỏc ACE là tam giỏc vuụng cõn.
b) Từ A hạ AH  BE, gọi M và N theo thứ tự là trung điểm của AH và HE. Chứng minh tứ giỏc BMNC là hỡnh 
bỡnh hành.
c) Chứng minh M là trực tõm của tam giỏc ANB.
d) Chứng minh ãANC 900.
3B. Cho tam giỏc ABC vuụng tại A. Về phớa ngoài tam giỏc, vẽ cỏc hỡnh vuụng ABDE, ACFG.
a) Chứng minh tứ giỏc BCGE là hỡnh thang cõn.
b) Gọi K là giao điểm của cỏc tia DE và FG, M là trung điểm của đoạn thẳng EG. Chứng minh ba điểm K, A, M 
thẳng hàng.
c) Chứng minh MA  BC.
d) Chứng minh DC, FB và AM đồng quy.
4. Cho hỡnh thoi ABCD, O là giao điểm của hai đường chộo. Vẽ đường thẳng qua B song song với AC, đường 
thẳng qua C song song với BD, hai đường thẳng đú cắt nhau ở K.
a) Tứ giỏc OBKC là hỡnh gỡ ?
b) Chứng minh AB = OK.
c) Tỡm điều kiện của hỡnh thoi ABCD để OBKC là hỡnh vuụng.
5. Cho hỡnh bỡnh hành ABCD cú BC = 2AB và Bã AC 600. Gọi E, F lần lượt là trung điểm của BC và AD.
a) Chứng minh tứ giỏc ECDF là hỡnh thoi.
b) Tứ giỏc ABED là hỡnh gỡ ?
c) Tớnh số đo của gúc ãAED.
6. Cho hỡnh thang ABCD (AB // CD). Gọi E, F theo thứ tự là trung điểm của AB, CD. Gọi O là trung điểm của EF. 
Qua O vẽ đường thẳng song song với AB, cắt AD và BC theo thứ tự tại M và N.
a) Tứ giỏc EMFN là hỡnh gỡ ?
b) Hỡnh thang ABCD cú thờm điều kiện gỡ để EMFN là hỡnh thoi.
c) Hỡnh thang ABCD cú thờm điều kiện gỡ để EMFN là hỡnh vuụng.
7. Cho tam giỏc ABC vuụng tại A, đường trung tuyến AM. Gọi H là điểm đối xứng vớ M qua AB, E là giao điểm 
của MH và AB. Gọi L là điểm đối xứng với M qua AC, F là giao điểm của MK và AC.
a) Xỏc định dạng của tứ giỏc AEMF, AMBH, AMCK. b) Chứng minh H đối xứng với K qua A.
c) Tam giỏc vuụng ABC cú thờm điều kiện gỡ thỡ AEMF là hỡnh vuụng ?
8. Trờn cỏc cạnh của một hỡnh bỡnh hành, dựng về phớa ngoài nú cỏc hỡnh vuụng. Chứng minh rằng nếu nối tõm 
cỏc hỡnh vuụng này, ta được một hỡnh vuụng.
HƯỚNG DẪN
 1A. a) Áp dụng tớnh chất của tam giỏc cõn cho ABC ta cú: AM  MC và BM = MC
 I là trung điểm của AC và K đối xứng với M qua I nờn tứ giỏc AMCK là hỡnh bỡnh 
 hành
 Lại cú MK = AC (=2MI)
 Tứ giỏc AMCK là hỡnh chữ nhật.
 b) Vỡ tứ giỏc AMCK là hỡnh chữ nhật (chứng minh ở a) AK//MC và AK = MC = MB 
 nờn tứ giỏc AKMB là hỡnh bỡnh hành.
 c) Nếu tứ giỏc AKMB là hỡnh thoi thỡ BA = AK = KM= MB.
 MBA cõn tại B Bã AM ãAMB = 900 vụ lý.
 Vậy khụng cú trường hợp nào của ABC để AKMB là hỡnh thoi.
 1B. a)Vỡ E đối xứng với điểm M qua điểm D nờn M,D,E thẳng hàng và DM = DE (1)
 Áp dụng tớnh chất đường trung bỡnh cho BAC ta cú DM//AC.
 Mà ABC vuụng tại A nờn CA  AB MD  AB (2)
 Từ (1) và (2) E đối xứng với M qua đường thẳng AB.
 b) Tứ giỏc AEMC là hỡnh bỡnh hành, tứ giỏc AEBM là hỡnh thoi.
 c) Chu vi tứ giỏc AEBM là 4BM = 8 (cm)
 d) nếu tứ giỏc AEBM là hỡnh vuụng thỡ ME = AB mà ME = AC (do ACME là hỡnh bỡnh 
 hành) AC = AB ABC vuụng cõn tại A.
 2A. a) DAE = BAF (c.g.c)
 Dã AE Bã AF và AE = AF
 Mà Eã AD Eã AB 900
 Eã AB Bã AF 900
 AEF vuụng cõn tại A.
 b) EAF vuụng cõn nờn IA = IE = FI (1); CFE vuụng cú IC là đường trung tuyến IE 
 = IC = IF (2);
 Từ (1) và (2) suy ra IA = IC nờn I thuộc trung trực của AC hay I thuộc BD.
 c) Do K đối xứng với A qua I nờn I là trung điểm của AK.
 Mà I là trung điểm của EF(gt) nờn AFKE là hỡnh bỡnh hành, AEF vuụng cõn tại A 
 nờn AI  EF.
 Vậy AFKE là hỡnh vuụng.
 2B. a) Bã AH Mã AC vỡ cựng phụ với ãABC à à
b) A1 C1 (1) (chứng minh a)
 à ả
Mà ABC vuụng cú AM là trung tuyến nờn AMC cõn tại M C1 A4 (2).
 à ả
Từ (1) và (2) suy ra A1 A4 (3)
D thuộc đường trung trực của BC.
 DM  BC = {M}
 ả ả
 D1 A2
 ả à ả à
Vỡ DM = MA (giả thiết) M1 A3 A2 A3 (4)
Từ (3) và (4) AD là phõn giỏc chung của Mã AH &Cã AB
c) Theo cỏch vẽ và kết quả cõu b), ta cú AEDF là hỡnh vuụng.
d) DBE = DCF (cạnh huyền - cạnh gúc vuụng)
3A. a) E là điểm đối xứng của điểm A qua điểm D A, D, E thẳng hàng và DA = DE 
 CD  AE tại trung điểm của AE CA = CE CAE cõn ở C.
 Dã AC = 450 ACE vuụng cõn.
b) Áp dụng tớnh chất đường trung bỡnh cho HAE và giả thiết ABCD là hỡnh vuụng 
ta sẽ chứng minh được tứ giỏc BMNC là hỡnh bỡnh hành.
c) Do AH  BN, mà NM//CB NM  AB nờn M là trực tõm của tam giỏc ANB.
d) M là trực tõm ABN nờn BM  AN mà BM//CN ãANC = 900
3B. a) Vỡ ABDE, ACFG là cỏc hỡnh vuụng nờn ta cú E, A, C thẳng hàng và B, A, G 
cũng thẳng hàng (1) và EC = BG.
Mà Eã BA ãAGC = 450 (2).
Từ (1) và (2)
Suy ra EB//CG & EC = BG EBCG là hỡnh thang cõn.
b) Chứng minh AEKG là hỡnh chữ nhật, mà M là trung điểm EG nờn K, A, M thẳng 
hàng.
c) Gọi H = MA  BC
Vỡ BEGC là hỡnh thang cõn nờn BEG = EBC (c-g-c) Eã CB Eã GB mà 
 Eã GA Mã AG Bã AH
 Bã AH ãABC Eã CB ãABC = 900 MA BC tại H.
d) ABK = BDC vỡ AB = DB, KA = EG = BC, Bã AK Dã BC Bã KA Bã CD mà KA  BC 
 CD  BK.
Chứng minh tương tự ta cũng cú BF  KC.
 KBC cosBF, CD, AM là 3 đường cao đồng quy tại trực tõm I.
4. a) BK//OC, CK//OB.
Mà OB OC OBKC là hỡnh chữ nhật.
b)ABCD là hỡnh thoi nờn AB = BC. OBKC là hỡnh chữ nhật nờn KO =BC.
 KO = BC ĐPCM. c) nếu OBKC là hỡnh vuụng thỡ OB = OC BD = AC. Vậy ABCD là hỡnh vuụng.
 1
5. a) Ta sẽ cú FD//EC và FD = EC = AD ECDF là hỡnh bỡnh hành.
 2
 1
Mà AB BC
 2
 AB = BE = EF = EC
 CDFE là hỡnh thoi.
b) Tứ giỏc ABED là hỡnh thang cõn vỡ BE//AD và Bã AD ãADE 600
 1 1
c) Ta cú EF CD AB CD AD , F là trung điểm AD ãAED 900 .
 2 2
a) ABCD là hỡnh thang nờn AE//DF AEFD là hỡnh thang. O là trung điểm EF, 
OM/AE M là trung điểm AD (tớnh chất đường trung bỡnh của hỡnh thang)
 1
 ME//FN//BD và ME = FN = AC AC = BD
 2
 ABCD là hỡnh thang cõn.
c) Nếu EMFN là hỡnh vuụng thỡ ME  EN BD  AC nờn ABCD là hỡnh thang cõn 
cú hai đường chộo vuụng gúc.
7. a) AMBH là hỡnh thoi (tứ giỏc cú hai đường chộo vuụng gúc với nhau tại trung 
điểm mỗi đường)
Tương tự cũng cú AMCK là hỡnh thoi. AEMF là hỡnh chữ nhật (tứ giỏc cú ba gúc 
vuụng).
b) Áp dụng tớnh chất đối xứng trục ta cú:
 à ả à ả
 AH AM , A1 A2 và AK AM , A3 A4 .
 ả à 0
Mà A2 A3 = 90 H, A, K thẳng hàng.
Lại cú AH = AM = AK H đối xứng với K qua A.
c) Nếu AEMF là hỡnh vuụng thỡ AM là đường phõn giỏc của Bã AC mà AM là đường 
trung tuyến.
 ABC vuụng cõn tại A.
8. Chỳ ý Kã AF Tã CJ (2 cạnh tương ứng song song)
 ãABC ãADC (gúc đối của hỡnh bỡnh hành)
 Fã AK ãABC (cú cạnh tương ứng vuụng gúc)
Suy ra Kã AF Tã CJ = ãABC ãADC
Vậy Mã AQ Mã BN Pã CN Pã DQ
Lại cú: MA = MB = PC=PD và AQ = BN = CN = DQ
(nửa đường chộo của hỡnh vuụng bằng nhau)
Suy ra MAQ = MBN = PCN = PDQ
 MQ = MN = NP = PQ (1) Do cỏc tam giỏc bằng nhau Bã NM Cã NP hay ãBNC Mã NP = 900 (2).
 Từ (1) và (2) cú MNPQ là hỡnh vuụng.
ĐỀ 2.Nõng Cao
Bài 1: Cho hỡnh bỡnh hành ABCD. Gọi K, I lần lượt là trung điểm của cỏc cạnh AB, CD. Đường chộo BD cắt AI 
ở M và cắt CK ở N. Chứng minh rằng:
a) AI // KC, AI KC.
b) ADM CBN.
c) KMIN, AMCN là cỏc hỡnh bỡnh hành.
d) DM MN NB.
 ã 0
Bài 2: Cho hỡnh bỡnh hành ABCD cú BC 2AB và BAD 60 . Gọi E, F lần lượt là trung điểm của BC và AD.
a) Chứng minh tứ giỏc ECDF là hỡnh thoi.
b) Tứ giỏc ABED là hỡnh gỡ?
c) Tớnh số đo của gúc ãAED.
Bài 3: Cho hỡnh thoi ABCD, O là trung điểm của hai đường chộo. Vẽ đường thẳng qua
 B song song với AC, đường thẳng qua C song song với BD, hai đường thẳng đú
cắt nhau ở K.
a) Tứ giỏc OBKC là hỡnh gỡ?
b) Chứng minh AB OK.
c) Tỡm điều kiện của hỡnh thoi ABCD để OBKC là hỡnh vuụng.
Bài 4: Cho hỡnh vuụng ABCD. E là điểm trờn cạnh DC, F là điểm trờn tia đối của tia BC sao cho BF DE.
a) Chứng minh tam giỏc AEF vuụng cõn. b) Gọi I là trung điểm của EF. Chứng minh I thuộc BD.
c) Lấy điểm K đối xứng với A qua I. Chứng minh tứ giỏc AEKF là hỡnh vuụng.
Bài 5: Cho hỡnh thoi ABCD cú Bà 600. Kẻ AE⊥ DC, AF ⊥ BC.
a) Chứng minh AE AF;
b) Chứng minh tam giỏc AEF đều;
c) Biết BD 16 cm, tớnh chu vi tam giỏc AEF.
Bài 6: Cho tam giỏc ABC, đường cao AH. Gọi I là trung điểm của AC. Lấy E là điểm đối xứng với H qua I. 
Gọi M , N lần lượt là trung điểm của HC, CE. Cỏc đường thẳng AM , AN cắt HE tại G và K.
a) Chứng minh tứ giỏc AHCE là hỡnh chữ nhật.
b) Chứng minh HG GK KE.
c) Tứ giỏc INMH là hỡnh gỡ? Vỡ sao?
Bài 7: Cho tam giỏc ABC cú đường cao AI. Từ A kẻ tia Ax vuụng gúc với AC, từ B kẻ tia By song song với 
 AC. Gọi M là giao điểm của tia Ax và tia By. Nối M với trung điểm P của AB, đường MP cắt AC tại Q và 
 BQ cắt AI tại H .
a) Tứ giỏc AMBQ là hỡnh gỡ?
b) Chứng minh rằng CH ⊥ AB.
c) Chứng minh tam giỏc PIQ cõn.
Bài 8: Cho hỡnh bỡnh hành ABCD. Trờn cỏc cạnh AB và CD lần lượt lấy cỏc điểm M và N sao cho AM DN. 
Đường trung trực của BM lần lượt cắt cỏc đường thẳng MN và BC tại E và F.
a) Chứng minh E và F đối xứng với nhau qua AB;
b) Chứng minh tứ giỏc MEBF là hỡnh thoi;
c) Hỡnh bỡnh hành ABCD cú thờm điều kiện gỡ để tứ giỏc BCNE là hỡnh thang cõn.
Bài 9: Cho tam giỏc ABC, vẽ ra phớa ngoài tam giỏc cỏc hỡnh vuụng ABDE và BCKH. BM là đường trung tuyến 
của tam giỏc ABC.
a) Chứng minh Dã BH ãABC 1800.
b) Vẽ hỡnh bỡnh hành DBHN. Chứng minh ABC NHB.
c) Chứng minh DH 2BM.
d) Chứng minh BM ⊥ DH.
Bài 10: Cho hỡnh vuụng ABCD. Gọi O là giao điểm hai đường chộo của hỡnh vuụng. Kẻ OF ⊥ AD, OG⊥ CD. 
Chứng minh;
a) Tứ giỏc OFDG là hỡnh gỡ? Vỡ sao? b) OB FG và OB⊥ FG;
c) Cỏc đường thẳng BO, AG, CF đồng quy.
ĐÁP ÁN THAM KHẢO
Bài 1: Cho hỡnh bỡnh hành ABCD. Gọi K, I lần lượt là trung điểm của cỏc cạnh AB, CD. Đường chộo BD cắt AI 
ở M và cắt CK ở N. Chứng minh rằng:
a) AI // KC, AI KC.
b) ADM CBN.
c) KMIN , AMCN là cỏc hỡnh bỡnh hành.
d) DM MN NB.
Giải
a) Chứng minh AICK là hỡnh bỡnh hành (2 cạnh đối AK, IC song song và bằng nhau) rồi suy ra ĐPCM.
b) AICK là hỡnh bỡnh hành suy ra ADI CBK c c c ADM CBN g c g 
 1 1
c) KN AM , MI NC, AM NC ADM CBN KN MI
 2 2
Mà KN // MI nờn tứ giỏc KMIN là hỡnh bỡnh hành.
 AMCN là cỏc hỡnh bỡnh hành vỡ AM NC và AM // NC.
d) Từ cõu a) suy ra DM NB mà MN NB ( định lớ đường trung bỡnh trong AMB )
Do đú DM MN NB.
Bài 2: Cho hỡnh bỡnh hành ABCD cú BC 2AB và Bã AD 600. Gọi E, F lần lượt là trung điểm của BC và AD.
a) Chứng minh tứ giỏc ECDF là hỡnh thoi.
b) Tứ giỏc ABED là hỡnh gỡ?
c) Tớnh số đo của gúc ãAED. Giải
 1 
a) Ta cú FD // EC, FD EC AD nờn ECDF là hỡnh bỡnh hành.
 2 
 1 1
Mà AB BC AD
 2 2
 AB BE EF EC
 ECDF là hỡnh thoi.
 1 1
b) Vỡ ECDF là hỡnh thoi nờn ãADE ãADC . 1800 600 600 .
 2 2
 ã ã 0
Tứ giỏc ABED là hỡnh thang cõn vỡ BE // AD và BAD ADE 60 .
c) Ta cú EF là đường trung bỡnh của hỡnh bỡnh hành ABCD nờn EF CD FD mà F là trung điểm AD nờn 
 EF FD AF.
Suy ra AED vuụng tại E.
Suy ra ãAED 900.
Bài 3: Cho hỡnh thoi ABCD , O là trung điểm của hai đường chộo. Vẽ đường thẳng qua
 B song song với AC, đường thẳng qua C song song với BD, hai đường thẳng đú
cắt nhau ở K.
a) Tứ giỏc OBKC là hỡnh gỡ?
b) Chứng minh AB OK.
c) Tỡm điều kiện của hỡnh thoi ABCD để OBKC là hỡnh vuụng.
Giải