Đề cương ôn tập môn Hình học Lớp 8 - Bài 7: Trường hợp đồng dạng thứ ba

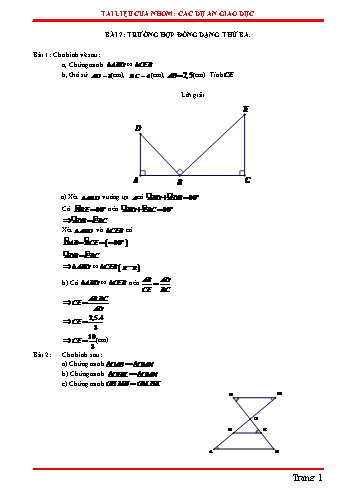
 TÀI LIỆU CỦA NHểM: CÁC DỰ ÁN GIÁO DỤC
 BÀI 7: TRƯỜNG HỢP ĐỒNG DẠNG THỨ BA.
Bài 1: Cho hỡnh vẽ sau:
 a, Chứng minh ABD ∽ CEB .
 b, Giả sử AD 3(cm), BC 4 (cm), AB 2,5(cm). TớnhCE .
 Lời giải
 E
 D
 A B C
 a) Xột ABD vuụng tại A cú ãABD ãADB 90
 Cú Dã BE 90 nờn ãABD Eã BC 90
 ãADB Eã BC
 Xột ABD và CEB cú 
 Dã AB Bã CE 90 
 ãADB Eã BC
 ABD ∽ CEB g g .
 AB AD
 b) Cú ABD ∽ CEB nờn 
 CE BC
 AB.BC
 CE 
 AD
 2,5.4
 CE 
 3
 10
 CE (cm)
 3
Bài 2: Cho hỡnh sau:
 a) Chứng minh OAB ∽ OMN .
 b) Chứng minh OHK ∽ OMN .
 c) Chứng minhOH.MN OM.HK
 N M
 O
 H K
 A B
 Trang 1 TÀI LIỆU CỦA NHểM: CÁC DỰ ÁN GIÁO DỤC
 Lời giải
 a) Xột OAB và OMN cú:
 Oã AB Nã MO ( gt)
 ãAOB Mã ON ( hai gúc đối đỉnh) 
 Do đú OAB ∽ OMN (g-g) 
 b) Xột OHK và OMN cú:
 Oã KH Mã NO ( gt)
 Hã OK Mã ON ( hai gúc đối đỉnh) 
 Do đú OHK ∽ OMN (g-g) 
 c) Vỡ OHK ∽ OMN
 OH HK
 ( 2 cạnh tương ứng) 
 OM MN
 OH.MN OM.HK
Bài 3: Cho ABC . Trờn tia đối của tia AB lấy điểm D , trờn tia đối của tia AC lấy điểm E sao 
 cho ãADE ãACB .
 a) Chứng minh ADE ∽ ACB và viết tỉ số đồng dạng.
 b) Chứng minh AD.AB AE.AC .
 Lời giải
 a) Xột ADE và ACB cú:
 ãADE ãACB (gt)
 Eã AD Bã AC (2 gúc đối đỉnh)
 ADE ∽ ACB ( g-g)
 AD AE DE
 ( cặp cạnh tương ứng) 
 AC AB CB
 AD AE
 b) Vỡ AD.AB AE.AC
 AC AB
Bài 4: Cho ABC cú AB AC , Trờn AC lấy điểm D sao cho ãABD ãACB .
 a) Chứng minh rằng ABD ∽ ACB
 b) Chứng minh AB2 AD.AC
 Trang 2 TÀI LIỆU CỦA NHểM: CÁC DỰ ÁN GIÁO DỤC
 Lời giải
 a) Xột ABD và ACB cú
 ãABD ãACB (gt)
 àA chung
 ABD ∽ ACB (g-g)
 AB AD
 b) Vỡ ABD ∽ ACB ( cỏc cạnh tương ứng)
 AC AB
 AB.AB AC.AD AB2 AC.AD
Bài 5: Cho ABC nhọn cú AB 2cm, AC 4cm . Trờn cạnh AC lấy điểm M sao cho gúc 
 ãABM ãACB .
 a) Chứng minh ABM ∽ ACB .
 b) Tớnh độ dài AM .
 Lời giải
 a) Xột ABM và ACB cú:
 ãABM ãACB (gt)
 àA chung
 ABM ∽ ACB (g-g)
 AM AB
 b) Vỡ ABM ∽ ACB ( cặp cạnh tương ứng)
 AB AC
 AB2 4
 AM 1cm
 AC 4
Bài 6: Cho ABC vuụng tại A cú Bà 600 , BD là phõn giỏc Bà .
 a) Tớnh số đo ãACB
 b) Chứng minh rằng ABC ∽ ADB .
 c) Biết độ dài AC 18cm . Tớnh BD .
 Trang 3 TÀI LIỆU CỦA NHểM: CÁC DỰ ÁN GIÁO DỤC
 B
 A D C
 Lời giải
 a) Xột ABC cú àA 900 nờn Bà Cà 900 ãACB 300
 b) Vỡ BD là phõn giỏc của Bà nờn
 1
 ãABD Dã BC ãABC 300
 2
 Xột ABC và ADB cú:
 ãABD ãACB 300
 àA chung
 ABC ∽ ADB ( g-g)
 BC AC AB.BC
 c) Vỡ ABC ∽ ADB BD 
 BD AB AC
 Xột ABC cú àA 900 ,Cà 300 nờn BC 2AB
 Áp dụng định lớ Pytago vào ABC cú:
 BC 2 AB2 AC 2 2AB 2 AB2 182 3AB2 324 AB 108cm
 BC 2. 108cm
 AB.BC 2.108
 Từ đú BD 12cm
 AC 18
Bài 7: ChoDABC cú đường phõn giỏc trong AD . Trờn tia đối của tia DA lấy điểm E sao cho 
 EãCD = BãAD .
 a) Chứng minh AD.DE = BD.CD .
 b) Chứng minh AD.AE = AB.AC .
 c) AD2 = AB.AC - BD.CD .
 Lời giải
 A
 B D C
 E
 a) Xột ABD và DCE cú:
 + BãAD = EãCD ( giả thiết )
 + ãADB Cã DE ( hai gúc đối đỉnh)
 Suy ra: ADB ∽ CDE
 Trang 4 TÀI LIỆU CỦA NHểM: CÁC DỰ ÁN GIÁO DỤC
 AD DB
 ị =
 CD DE
 ị AD.DE = DB.CD
 Vậy AD.DE = BD.CD .
 b) Ta cú tam giỏc ADB ∽ CDE
 ị ãABD = CãED .
 Ta cú AD là đường phõn giỏc trong của ΔABD Bã AD = Dã AC hay Bã AD = Eã AC .
 Xột ABD và ACE , cú:
 + ãABD = CãED
 + Bã AD = Eã AC
 Suy ra: ABD ∽ AEC
 AB AD
 ị =
 AE AC
 ị AB.AC = AD.AE
 Vậy AD.AE = AB.AC .
 c) Ta cú: AD.DE = BD.CD ( cõu a ) (1).
 AD.AE = AB.AC ( cõu b ) (2).
 Từ (1) và (2)suy ra: AD.AE - AD.DE = AB.AC - BD.CD
 ị AD.(AE - DE)= AB.AC - BD.CD
 ị AD.AD = AB.AC - BD.CD
 ị AD2 = AB.AC - BD.CD
 Vậy AD2 = AB.AC - BD.CD .
Bài 8: ChoDABC phõn giỏc trong AD . Trờn nửa mặt phẳng bờ BC khụng chứa A , vẽ CãBx = BãAD . 
 Bx cắt AD tại điểm E . Chứng minh: 
 a ADC ∽ BDE
 b) ÃBE = ãADC
 c) EA.BD2 = ED.AB2 .
 Lời giải
 A
 C
 B D
 E
 x
 a) Cú AD là phõn giỏc trong của ΔABC ị BãAD = DãAC .
 Mà CãBx = BãAD ( gt ), suy ra CãBx = DãAC hay DãBE = DãAC .
 Xột ΔADC và ΔBDE cú: 
 + DãAC = DãBE
 + ãADC = BãDE ( hai gúc đối đỉnh )
 Suy ra: ADC ∽ BDE ( g – g).
 Trang 5 TÀI LIỆU CỦA NHểM: CÁC DỰ ÁN GIÁO DỤC
 b) Xột ΔADB cú ãADC là gúc ngoài tại đỉnh D.
 Suy ra: ãADC = BãAD + ãABD
 Mà ÃBE = ãABD + DãBE; DãBE = BãAD(= DãAC).
 Do vậy ÃBE = ãADC .
 c) Xột ΔABE và ΔBDE cú: 
 + BãAE = DãBE
 + Eà chung
 Suy ra: ABE ∽ BDE ( g – g).
 AB AE BE
 Suy ra: = = = k .
 BD BE DE
 2
 ổABử AE BE AE 2 2 2
 Do đú: ỗ ữ = . = = k ị EA.BD = ED.AB .
 ốỗBDứữ BE DE DE
Bài 9: ChoDABC vuụng tại A , cú AH là đường cao, BD là đường phõn giỏc. Gọi I là giao điểm 
 của AH và BD . 
 a) Chứng minh ΔABD ∽ ΔHBI
 b) Chứng minh DADI cõn.
 c) Chứng minh IH.DC = IA.DA .
 Lời giải
 A
 D
 I
 B H C
 a) Cú BD là đường phõn giỏc của ΔABC , H ẻ BC; I ẻ BD ị ãABI = Hã BI .
 Cú AH là đường cao của ΔABC , I ẻ AH ị IãHB = 900 .
 Cú ΔABC vuụng tại A nờn BãAC = 900 .
 Xột ΔABC và ΔHBI cú:
 + BãAC = IãHB = 900
 + ãABI = Hã BI
 Suy ra: ABD ∽ HBI
 b) Cú ABD∽ HBI ( cõu a ) suy ra ãADB = BãIH ( hai gúc tương ứng ).
 Mà BãIH = Dã IA ( hai gúc đối đỉnh).
 Suy ra: ãADB = Ã ID hay ÃDI = Ã ID .
 Xột ΔADI cú ÃDI = Ã ID nờn ÃDI = Ã ID cõn tại A.
 c) 
 XộtDABC và DABH cú:
 + BãAC = ãAHB = 900
 + Bàchung
 Suy ra: ABC ∽ HBA ( g – g )
 Trang 6 TÀI LIỆU CỦA NHểM: CÁC DỰ ÁN GIÁO DỤC
 AB BC BA BH
 ị = ị = (1)
 BH BA BC BA
 IH BH
 Cú BI là đường phõn giỏc của ΔABH nờn suy ra = ( Tớnh chất đường phõn giỏc ) 
 IA BA
 (2).
 DA BA
 Cú BD là đường phõn giỏc của ΔABC nờn suy ra = ( Tớnh chất đường phõn giỏc ) 
 DC BC
 (3).
 IH DA
 Từ (1), (2) và (3) suy ra = .
 IA DC
 Do vậy IH.DC = IA.DA
Bài 10: Cho ΔECD . Trờn cỏc cạnh ED , EC lần lượt lấy cỏc điểm A và B sao cho EãAB = EãCD . Gọi 
 O là giao điểm của AC và BD . 
 a) Chứng minh EAB ∽ ECD .
 b) Chứng minh EAC ∽ EBD
 c) Chứng minh OA.OC = OB.OD .
 Lời giải
 E
 A
 B
 O
 C
 D
 a) XộtDEBA và DECD cú:
 + EãAB = EãCD
 + ãAEB chung
 Suy ra: EAB ∽ ECD ( g - g ).
 EA EB
 b) Cú D EAB ∽ DECD ị =
 EC ED
 EA EC
 ị =
 EB ED
 XộtDEAC và DEBD cú:
 + ãAEB chung
 EA EC
 + =
 EB ED
 Suy ra: EAC ∽ EBD ( c- g - c ).
 c) CúDEAC ∽ DEBD ị EãCA = EãDB ( hai gúc tương ứng ) hay BãCO = ãADO .
 XộtDOBC và DODA cú:
 + BãCO = ãADO (chứng minh trờn )
 + BãOC = ãAOD ( hai gúc đối đỉnh )
 Suy ra: OCB ∽ ODA ( g - g )
 Trang 7 TÀI LIỆU CỦA NHểM: CÁC DỰ ÁN GIÁO DỤC
 OB OC
 ị =
 OA OD
 ị OA . OC = OB . OD .
Bài 11: Cho ΔABC cú AB = 2 cm, AC = 4 cm. Qua B dựng đường thẳng cắt AC tại D sao cho 
 ãABD = ÃCB .
 a) Chứng minh ABD ∽ ACB .
 b) Tớnh AD và DC .
 c) Gọi AH là đường cao của ΔABC , AE là đường cao của ΔABD . Chứng minh rằng diện 
 tớch ΔABH gấp 4 lần diện tớch ΔADE .
 Lời giải
 B
 H
 E
 A C
 D
 a) XộtDABD và DABC cú:
 + BãAC chung
 + ãABD = ÃCB ( giả thiết )
 Suy ra: ABD ∽ ACB ( g - g ).
 b) Cú ABD ∽ ACB ( cõu a ).
 AB AD
 ị =
 AC AB
 AB2
 ị AD = . Mà AB = 2 cm, AC = 4 cm
 AC
 2.2
 Do đú AD = = 1 ( cm ).
 4
 Cú AC = AD + DC (D ẻ AC)
 Suy ra: DC = AC - AD = 4- 1= 3( cm ).
 Vậy AD = 1(cm), DC = 3(cm).
 c) Cú ABD ∽ ACB ( cõu a ).
 AD AB 2 1
 ị k = = = = .
 AB AC 4 2
 Mà AE là đường cao của DABD , và AH là đường cao của DACB .
 AE 1
 Do đú = k = .
 AH 2
 Cú AE là đường cao của DABD ị ãAED = 900 .
 Cú AH là đường cao củaDACB ị ãAHB = 900 .
 Cú D ABD ∽ DACB ị ãADB = ÃBC hay ãADE = ãABH .
 Xột DAED và DABH cú:
 + ãAED = ãAHB = 900
 Trang 8 TÀI LIỆU CỦA NHểM: CÁC DỰ ÁN GIÁO DỤC
 + ãADE = ãABH ( chứng minh trờn )
 Suy ra: AED ∽ AHB ( g - g )
 S ổAE ử2 ổ1ử2 1
 Do đú DAED = ỗ ữ = ỗ ữ =
 ỗ ữ ỗ ữ
 SDAHB ốAH ứ ố2ứ 4
 Vậy SDAHB = 4SDAED .
Bài 12: Cho ABC vuụng tại A cú đường cao AH , đường phõn giỏc BD cắt AH tại E . Chứng 
minh:
 a, ABD ∽ HBE 
 2
 b, AB BH.BC . B
 EH AD
 c, . H
 EA DC
 E
 A D C
 Lời giải 
 Chứng minh ABD ∽ HBE
 Xột ABD và HBE cú:
 Bã AD Bã HE 900
 ãABD Hã BE ( Do BD là tia phõn giỏc ãABC )
 Do vậy: ABD ∽ HBE ( g – g )
 Chứng minh: AB2 BH.BC
 Xột ABC và HBA cú:
 Bã AC Bã HA 900
 ãABC chung
 Do vậy: ABC ∽ HBA ( g – g ) nờn:
 AB BC
 AB2 BH.BC
 BH AB
 EH AD
 Chứng minh: 
 EA DC
 BD là đường phõn giỏc trong ABC nờn:
 AB AD
 (1)
 BC DC
 BE là đường phõn giỏc trong HBA nờn:
 Trang 9 TÀI LIỆU CỦA NHểM: CÁC DỰ ÁN GIÁO DỤC
 EH BH
 (2)
 EA BA
 AB BC AB BH
 Mà: (cmt) (3) 
 BH AB BC AB
 EH AD
 Từ (1)(2)(3) suy ra: 
 EA DC
Bài 13: Cho ABC cú Bà 2.Cà . Trờn tia đối của tia BA lấy điểm D sao cho BD BC.
 a, Chứng minh à CD à BC .
 b, Chứng minh AC2 AB.AD . Giả sử AB 4,BC 5 . Tớnh AC .
 A
 B C
 Lời giải 
 a) Chứng minh à CD à BC .
 Vỡ BC BD (gt) BCD cõn tại B .
 D
 Bã DC Bã CD
 ãABC là gúc ngoài của BCD nờn: ãABC Bã DC Bã CD
 ãABC 2Bã CD
 Mà ãABC 2ãACB (gt) ãACB Bã CD
 Ã CD Ã CB Bã CD 2Ã CB Ã BC
 b) Chứng minh: AC 2 AB.AD
 Xột ABC và ACD cú:
 ãABC ãACD (cmt)
 Cã AB chung
 Do vậy: ABC ∽ ACD ( g – g )
 AB AC
 AC 2 AB.AD
 AC AD
 Giả sử AB 4,BC 5ta cú:
 AC 2 AB.AD AB.(AB BD) 4.(4 5) 36
 AC 6
Bài 14: Cho ABC cõn tại A. Lấy D thuộc AB , M thuộc BC , E thuộc CA sao cho 
Dã ME Ã BC .
 a, Chứng minh Bã DM Cã ME .
 Trang 10