Tài liệu ôn tập môn Toán Lớp 8 - Bài 2: Hình thang

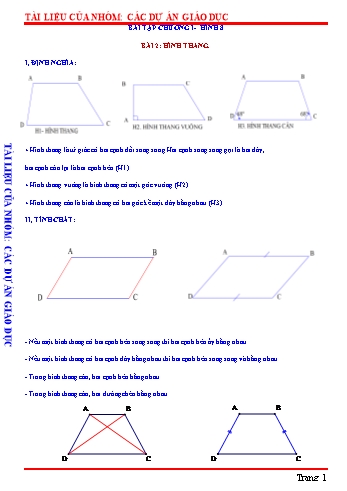
 TÀI LIỆU CỦA NHÓM: CÁC DỰ ÁN GIÁO DỤC
 BÀI TẬP CHƯƠNG I- HÌNH 8
 BÀI 2: HÌNH THANG.
 I, ĐỊNH NGHĨA:
TÀI LIỆU CỦA NHÓM: CÁC DỰ ÁN GIÁO DỤC
 + Hình thang là tứ giác có hai cạnh đối song song. Hai cạnh song song gọi là hai đáy, 
 hai cạnh còn lại là hai cạnh bên. (H1)
 + Hình thang vuông là hình thang có một góc vuông. (H2)
 + Hình thang cân là hình thang có hai góc kề một đáy bằng nhau. (H3)
 II, TÍNH CHẤT:
 - Nếu một hình thang có hai cạnh bên song song thì hai cạnh bên ấy bằng nhau.
 - Nếu một hình thang có hai cạnh đáy bằng nhau thì hai cạnh bên song song và bằng nhau.
 - Trong hình thang cân, hai cạnh bên bằng nhau.
 - Trong hình thang cân, hai đường chéo bằng nhau. 
 A
 A B B
 D C D C
 Trang 1 TÀI LIỆU CỦA NHÓM: CÁC DỰ ÁN GIÁO DỤC
 III, DẤU HIỆU NHẬN BIẾT:
 - Hình thang có hai góc kề một đáy bằng nhau là hình thang cân.
 - Hình thang có hai đường chéo bằng nhau là hình thang cân.
 IV, BÀI TẬP VẬN DỤNG:
 Bài 1: Cho hình thang ABCD có AD//BC , có Aˆ Bˆ 20 và Dˆ 2Cˆ .
 B C
 a) Tính Aˆ Bˆ .
TÀI LIỆU CỦA NHÓM: CÁC DỰ ÁN GIÁO DỤC
 b) Chứng minh Aˆ Bˆ Cˆ Dˆ .
 c) Tính số đo các góc của hình thang.
 A D
 Lời giải
 a) Vì AD//BC nên Aˆ Bˆ 180 (hai góc trong cùng phía bù nhau) 1 
 b) Vì AD//BC nên Cˆ Dˆ 180 (hai góc trong cùng phía bù nhau) 2 
 Từ 1 và 2 suy ra, Aˆ Bˆ Cˆ Dˆ (đpcm)
 c) Ta có: Aˆ Bˆ 180 ; Aˆ Bˆ 20
 Aˆ 100 ; Bˆ 80
 Tương tự ta có:Cˆ Dˆ 180 ; Dˆ 2Cˆ Cˆ 60 ; Dˆ 120
 Bài 2: Cho hình thang vuông ABCD có Aˆ Dˆ 90 , AB AD 4cm , DC 4cm và BH  CD tại 
 H . A B
 a) Chứng minh ABD HDB .
 b) Chứng minh BHC vuông cân tại H .
 D 4 cm C H
 Lời giải
 a) Ta có: AB//DC ·ABD B· DC (hai góc sole trong) hay ·ABD B· DH
 Trang 2 TÀI LIỆU CỦA NHÓM: CÁC DỰ ÁN GIÁO DỤC
 Xét ADB vuông tại A và HDB vuông tại H có :
 BD là cạnh chung
 ·ABD B· DH (cmt)
 ABD HDB (cạnh huyền – góc nhọn)
 b) Ta có : ABD HDB (cmt) AB DH; AD BH (hai cạnh tương ứng) 1 
 Lại có : DH DC CH AB 4 CH hay AB CH 4cm
TÀI LIỆU CỦA NHÓM: CÁC DỰ ÁN GIÁO DỤC Mà : AB AD 4cm AD BH 2 
 Từ 1 và 2 suy ra, BH CH
 BHC vuông cân tại H . 
 Bài 3: Cho ABC , các tia phân giác góc Bˆ,Cˆ cắt nhau tại I . Qua I kẻ đường thẳng song song với 
 BC cắt AB và lần lượt tại D và E . A
 a) Tìm các hình thang có trong hình.
 b) Chứng minh rằng : BID cân ở D và IEC cân ở E .
 D I E
 c) So sánh DE với tổng BD CE .
 B C
 Lời giải
 a) Các hình thang có trong hình là:
 BDIC DI //BC ;CEIB IE//BC ; DECB DE//BC 
 b, Ta có: DI //BC D· IB I·BC (sole trong)
 Mà D· BI I·BC ( BI là tia phân giác góc Bµ )
 D· IB D· BI
 BID cân ở D (đpcm)
 Ta có : IE//BC D· IB I·BC (sole trong)
 Mà E· IC I·CB (CI là tia phân giác góc Cµ )
 Trang 3 TÀI LIỆU CỦA NHÓM: CÁC DỰ ÁN GIÁO DỤC
 E· IC E· CI
 IEC cân ở E (đpcm)
 c, Ta có : BIDcân ở D (cmt) BD ID
 IEC cân ở E (cmt) IE CE
 Lại có : DE DI IE ( I nằm giữa D và E )
 DE BD CE
 ˆ ˆ
TÀI LIỆU CỦA NHÓM: CÁC DỰ ÁN GIÁO DỤC Bài 4: Cho hình thang ABCD có AB//DC và AB CD . Hai tia phân giác góc C và góc D cắt nhau 
 tại K thuộc đáy AB . Chứng minh rằng :
 A K B
 a) ADK cân ở A, BKC cân ở B .
 b) AD BC AB .
 D C
 Lời giải
 a) Ta có: AB//DC ·AKD K· DC (sole trong)
 Mà ·ADK K· DC ( DK là tia phân giác góc Dµ )
 ·AKD ·ADK
 ADK cân ở A (đpcm)
 Ta có : KB//DC B· KC K· CD (sole trong)
 Mà B· KC K· CD (CK là tia phân giác góc Cµ )
 B· KC B· CK
 BKC cân ở B (đpcm)
 b) Ta có : ADK cân ở A (cmt) AD AK
 BKC cân ở B (cmt) BK BC
 Lại có : AB AK KB (I nằm giữa D và E )
 AB AD BC (đpcm)
 Trang 4 TÀI LIỆU CỦA NHÓM: CÁC DỰ ÁN GIÁO DỤC
 Bài 5: Cho hình thang ABCD có AB//CD và CD AD BC . Gọi K là điểm thuộc đáy CD sao cho
 KD AD. Chứng minh rằng :
 A B
 a) AK là phân giác góc Aˆ .
 b) KC BC .
 c) BK là tia phân giác của góc Bˆ .
 D K C
 Lời giải
 a) Ta có :
TÀI LIỆU CỦA NHÓM: CÁC DỰ ÁN GIÁO DỤC
 AB//DC ·AKD K· AB (sole trong) 1 
 ADK có KD AD ADK cân tại D
 D· AK D· KA 2 
 Từ 1 và 2 suy ra, D· AK B· AK
 AK là tia phân giác góc Aˆ .
 b, Ta có: CD DK KC ( K nằm giữa D và C )
 DK AD
 DC AD KC
 Lại có : CD AD BC KC BC (đpcm)
 c, BKC có KC BC BKC cân tại C
 B· KC C· KB
 Lại có: AB//DC ·ABK B· KC (sole trong) 
 ·ABK K· BC hay BK là tia phân giác của góc Bˆ (đpcm)
 Bài 6: Cho ABC cân tại A, Hai đường trung tuyến BD và CE . Chứng minh 
 a) ADE cân tại A.
 b) ABD ACE .
 c) Tứ giác BCDE là hình thang cân.
 Trang 5 TÀI LIỆU CỦA NHÓM: CÁC DỰ ÁN GIÁO DỤC
 Lời giải
 a) ADE cân tại A. A
 AB AC
 Ta có AE EB ; AD DC ( BD, CE là trung tuyến )
 2 2
 Mà AB AC ( ABC cân tại A)
 AE AD ADE cân tại A. E D
 b) ABD ACE .
 Xét ABD và ACE ta có: 
 AB AC ( ABC cân tại A)
 µ
 A chung B C
 AE AD(chứng minh trên)
 ABD ACE ( c.g.c)
TÀI LIỆU CỦA NHÓM: CÁC DỰ ÁN GIÁO DỤC c) Tứ giác BCDE là hình thang cân.
 180 µA
 Ta có ·AED ·ADE ( vì ADE cân tại A)
 2
 180 µA
 ·ABC ·ACB ( vì ABC cân tại A)
 2
 ·AED ·ABC
 Mà hai góc này ở vị trí đồng vị ED // BC BEDC là hình thang 1 
 Lại có ·ABC ·ACB ( vì ABC cân tại A)
 Nên tứ giác BCDE là hình thang cân.
 Bài 7: Cho ABC cân tại A có BE và CF là hai đường phân giác. Chứng minh :
 a) AEF cân tại A.
 b) Tứ giác BCEF là hình thang cân.
 c) CE EF FB .
 Lời giải A
 a) AEF cân tại A.
 ·ABC
 Ta có: ·ABE E· BC ( vì BE là phân giác )
 2
 ·ACB E
 ·ACF F· CB ( vì CF là phân giác ) F
 2
 Mà ·ABC ·ACB ( vì ABC cân tại A)
 ·ABE ·ACF
 Xét ABE và ACF ta có: B C
 ·ABE ·ACF (chứng minh trên)
 AB AC ( ABC cân tại A)
 µA chung
 ABE ACF ( g.c.g) AE AF AEF cân tại A.
 b) Tứ giác BCEF là hình thang cân.
 180 µA
 Ta có ·AEF ·AFE ( vì AFE cân tại A)
 2
 Trang 6 TÀI LIỆU CỦA NHÓM: CÁC DỰ ÁN GIÁO DỤC
 180 µA
 ·ABC ·ACB ( vì ABC cân tại A)
 2
 ·AEF ·ABC
 Mà hai góc này ở vị trí đồng vị EF // BC BCEF là hình thang 
 Lại có ·ABC ·ACB ( vì ABC cân tại A)
 Nên tứ giác BCEF là hình thang cân.
 c) CE EF FB .
 Ta có: EF // BC F· EB E· BC (SO LE TRONG)
 Mà ·ABE E· BC ( vì BE là phân giác )
 F· EB F· BE EFB cân tại F BF EF 1 
TÀI LIỆU CỦA NHÓM: CÁC DỰ ÁN GIÁO DỤC Chứng minh tương tự ta có EF EC 2 
 Từ (1) và (2) CE EF FB . 
 Bài 8: Cho hình thang cân ABCD có AB ABCD // CD và AB CD , AB AD.
 a) Chứng minh A· DB B· DC .
 b) CA có phải là tia phân giác của góc Cµ không ? Vì sao ?
 Lời giải
 a) Chứng minh A· DB B· DC .
 A B
 Ta có AB // CD ·ABD B· DC ( so le trong)
 Lại có AB AD ABD cân tại A ·ABD ·ADB
 ·ADB C· DB
 b) CA có phải là tia phân giác của góc Cµ không ? Vì sao ?
 Ta có ABCD là hình thang cân BC AD mà AB AD D C
 AB BC ABC cân tại B
 B· AC B· CA
 Mặt khác B· AC ·ACD ( so le trong)
 B· CA ·ACD hay CA là tia phân giác của góc Cµ .
 Bài 9: Cho hình thang cân ABCD có AB // CD và AB CD . Gọi O là giao điểm của AD và BC . E là 
 giao điểm của AC và BD. Chứng minh :
 a) AOB cân tại O .
 b) ABD BAC .
 c) EC ED .
 d) OE là trung trực của hai đáy AB và CD .
 Lời giải
 a) Ta có ABCD là hình thang cân ·ADC B· CD hay O· DC O· CD AOB cân tại O .
 b) Xét ABD và BAC, có: O
 AB chung
 · ·
 BAD ABC ( ABCD là hình thang cân )
 A BTrang 7
 E
 D C TÀI LIỆU CỦA NHÓM: CÁC DỰ ÁN GIÁO DỤC
 AD BC ( ABCD là hình thang cân )
 ABD BAC (c.g.c)
 c) Ta có:
 ·ADC B· CD ( ABCD là hình thang cân )
 ·ADB B· CA( ABD BAC )
 ·ADC ·ADB B· CD B· CA B· DC ·ACD hay E· DC E· CD
 EDC cân tại E EC ED .
 d) +) Ta có :
 AD BC ( ABCD là hình thang cân )
 OA OB ( AOB cân tại O )
 OA AD OB BC hay OD OC O nằm trên đường trung trực của CD 1
TÀI LIỆU CỦA NHÓM: CÁC DỰ ÁN GIÁO DỤC 
 +) EC ED E nằm trên đường trung trực của CD 2 
 +) AC BD ( ABCD là hình thang cân )
 EC ED (cmt)
 AC EC BD ED EA EB E nằm trên đường trung trực của AB 3 
 +) AOB cân tại O OA OB O nằm trên đường trung trực của AB 4 
 Từ 1 , 2 , 3 và 4 OE là trung trực của hai đáy AB và CD .
 Bài 10: Cho hình thang cân ABCD có AD // BC và Aµ 600 , AD 4cm , BC 2cm . Qua B kẻ đường 
 thẳng song song vớiCD cắt AD tại E .
 a) Tính ED.
 b) Chứng minh ABE đều.
 c) Kẻ BH  AD ở H . Tính AH .
 Lời giải
 a) Tính ED.
 B 2 cm C
 Ta có AD // BC hay ED // BC mà BE // DC
 ED BC 2 cm( hình thang có hai cạnh bên song song thì 
 hai cạnh đáy, hai cạnh bên bằng nhau)
 b) Chứng minh ABE đều.
 600
 Ta có : AB CD (Vì ABCD là hình thang cân)
 A H E D
 BE CD ( hình thang có hai cạnh bên song song thì hai 
 cạnh đáy, hai cạnh bên bằng nhau) 4 cm
 BA BE ABE cân tại B , lại có Aµ 600
 ABE đều.
 c) Kẻ BH  AD ở H . Tính AH .
 Ta có AE AD ED 4 2 2cm
 AE 2
 ABE đều nên đường cao BH đồng thời là đường trung tuyến AH 1cm
 2 2
 Trang 8 TÀI LIỆU CỦA NHÓM: CÁC DỰ ÁN GIÁO DỤC
 Bài 11: Cho hình thang cân ABCD có AB // CD và AD BC . AH và BK là các đường cao. Chứng 
 minh 
 a, AHD BKC .
 CD AB
 b, DH .
 2
 Lời giải
 A B
TÀI LIỆU CỦA NHÓM: CÁC DỰ ÁN GIÁO DỤC
 D H K C
 a) Vì tứ giác ABCD là hình thang cân nên AD BC ; A· DC B· CD
 Xét AHD và BKC có:
 AD = BC ( tứ giác ABCD là hình thang cân)
 ·ADH B· CK ( tứ giác ABCD là hình thang cân)
 A· HD B· KC 900 (vì AH  DC;BK  DC )
 Vậy AHD BKC ( cạnh huyền – góc nhọn)
 b) Ta có: AHD BKC nên DH KC (hai cạnh tương ứng)
 Xét hình thang ABHK (do AB // HK )
 Có AH // BK (do cùng vuông góc với DC )
 Nên : AB HK
 Có: DH KC DC HK DC AB
 2DH DC AB
 DC AB
 Hay DH 
 2
 Bài 12: Cho hình thang cân ABCD có AD // BC và AD BC , AD AB . Kẻ DE // AB, DH  BC
 ( E và H thuộc BC ). Biết AD 5cm , DH 4cm .
 a, Tính EC .
 b, Tính BC .
 c, Chứng minh DAE BEA .
 Lời giải
 A 5 cm D
 4 cm
 B E H C
 Trang 9 TÀI LIỆU CỦA NHÓM: CÁC DỰ ÁN GIÁO DỤC
 a) Xét hình thang ADEB ( AD // BE)
 Có AB // DE (gt) 
 Nên : AD BE 5(cm) ; AB DE 5(cm) (Tính chất hình thang)
 Ta có: AB DE ; AB DC ( hình thang ABCD cân)
 Suy ra: DE = DC DEC cân tại D
 Xét DEC có DH là đường cao đồng thời là đường trung tuyến
 Suy ra: HC = HE (tính chất tam giác cân) 
 Xét DHC vuông tại H ( DH  BC ). Áp dụng định lý Pitago ta có:
 DC 2 DH 2 HC 2 
 52 42 HC
 HC 2 52 42
TÀI LIỆU CỦA NHÓM: CÁC DỰ ÁN GIÁO DỤC
 HC 2 9
 Suy ra: HC 3(cm) (cm)
 Vậy EC 2HC 6(cm)
 b) BC BE EC 5 6 11(cm)
 c) Xét DAE và BEAcó:
 AD = BE (chứng minh trên)
 D· AE ·AEB ( hai góc so le trong vì ( AD // BE)
 Cạnh AE : chung
 Vậy DAE = BEA(c – g – c)
 Trang 10