Tài liệu ôn tập môn Toán Lớp 8 - Bài 3: Đối xứng trục, đối xứng tâm. Hình bình hành

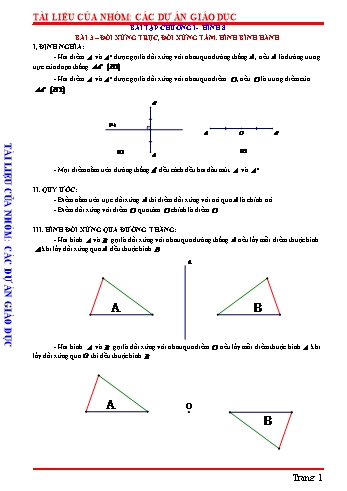
 TÀI LIỆU CỦA NHÓM: CÁC DỰ ÁN GIÁO DỤC
 BÀI TẬP CHƯƠNG I- HÌNH 8
 BÀI 3 – ĐỐI XỨNG TRỤC, ĐỐI XỨNG TÂM. HÌNH BÌNH HÀNH
 I, ĐỊNH NGHĨA:
 - Hai điểm A và A' được gọi là đối xứng với nhau qua đường thẳng d , nếu d là đường trung 
 trực của đoạn thẳng AA'. H1 
 - Hai điểm A và A' được gọi là đối xứng với nhau qua điểm O , nếu O là trung điểm của 
 AA'. H 2 
 A'
 ( d )
 A O A'
TÀI LIỆU CỦA NHÓM: CÁC DỰ ÁN GIÁO DỤC
 H2
 H1 A
 - Mọi điểm nằm trên đường thẳng d đều cách đều hai đầu mút A và A' .
 II. QUY ƯỚC:
 - Điểm nằm trên trục đối xứng d thì điểm đối xứng với nó qua d là chính nó.
 - Điểm đối xứng với điểm O qua tâm O chính là điểm O .
 III. HÌNH ĐỐI XỨNG QUA ĐƯỜNG THẲNG:
 - Hai hình A và B gọi là đối xứng với nhau qua đường thẳng d nếu lấy mỗi điểm thuộc hình 
 A khi lấy đối xứng qua d đều thuộc hình B .
 d
 A B
 - Hai hình A và B gọi là đối xứng với nhau qua điểm O nếu lấy mỗi điểm thuộc hình A khi 
 lấy đối xứng qua O thì đều thuộc hình B .
 A O
 B
 Trang 1 TÀI LIỆU CỦA NHÓM: CÁC DỰ ÁN GIÁO DỤC
 IV, ĐỊNH NGHĨA:
 A B
 - Tứ giác có các cặp cạnh đối song song là hình bình hành. H1 
 AB//CD
 - ABCD là hình bình hành 
 AD//CB
 D C
 H1
 V, TÍNH CHẤT:
 - Trong hình bình hành các cạnh đối song song và bằng nhau.
 - Trong hình bình hành các góc đối bằng nhau.
TÀI LIỆU CỦA NHÓM: CÁC DỰ ÁN GIÁO DỤC - Trong hình bình hành hai đường chéo cắt nhau tại trung điểm của mỗi đường.
 VI, DẤU HIỆU NHẬN BIẾT:
 - Tứ giác ABCD là HBH nếu các cạnh đối song song.
 - Tứ giác ABCD là HBH nếu các cạnh đối bằng nhau.
 - Tứ giác ABCD là HBH nếu các góc đối bằng nhau.
 - Tứ giác ABCD là HBH nếu hai đường chéo cắt nhau tại trung điểm của mỗi đường.
 - Tứ giác ABCD là HBH nếu hai cạnh đối vừa song song vừa bằng nhau.
 VII, BÀI TẬP VẬN DỤNG:
 1
 Bài 1: Cho hình thang ABCD có AB//CD và AB CD . Gọi E là trung điểm của CD . 
 2
 a) Chứng minh tứ giác ABED là hình bình hành.
 b) Chứng minh tứ giác ABCE là hình bình hành.
 Lời giải
 A B
 D E C
 1 1
 a) Vì E là trung điểm của CD nên DE CE CD mà AB CD nên AB DE CE . 
 2 2
 Do đó AB DE 1 
 Mặt khác ta có AB//CD nên AB//DE 2 
 Từ 1 và 2 suy ra tứ giác ABED là hình bình hành.
 b) Xét tứ giác ABCE có: AB CE (Chứng minh trên)
 AB//CE ( vì AB//CD ) 
 Do đó tứ giác A B C E là hình bình hành.
 Trang 2 TÀI LIỆU CỦA NHÓM: CÁC DỰ ÁN GIÁO DỤC
 Bài 2: Cho ABC có D, E, F lần lượt là trung điểm các cạnh BC, AC, AB . 
 a) Chứng minh DE//AF và DE AF .
 b) Chứng minh tứ giác AEDF là hình bình hành.
 Lời giải
 A
 F E
TÀI LIỆU CỦA NHÓM: CÁC DỰ ÁN GIÁO DỤC
 B D C
 a) Xét ABC có D , E lần lượt là trung điểm các cạnh BC , AC nên DE là đường trung 
 1
 bình. Do đó DE//AB và DE AB .
 2
 1
 Mà F là trung điểm của AB nên AF BF AB
 2
 Vậy DE//AF và DE AF .
 b) Xét tứ giác AEDF có: DE//AF (Chứng minh trên)
 DE AF (Chứng minh trên)
 Do đó tứ giác A E D F là hình bình hành.
 Bài 3: Cho ABC cân ở A có điểm M trên cạnh BC . Kẻ MD//AC và ME//AB D AB, E AC .
 a) Chứng minh ADME là hình bình hành.
 b) EMC là tam giác gì? 
 c) So sánh MD ME với AC .
 Lời giải
 a) Xét tứ giác ADME có: DM //AE ( vì MD//AC , E AC ) A
 ME//AD (vì ME//AB , D AB )
 Do đó tứ giác A D M E là hình bình hành.
 µ µ · µ
 b) Vì ABC cân ở A nên B C mà ME//AB nên EMC B (hai góc đồng vị). E
 Do đó E· MC Cµ suy ra EMC là tam giác cân tại E .
 c) Ta có MD AE ( vì tứ giác ADME là hình bình hành) D
 Mặt khác, ME EC ( vì EMC là tam giác cân tại E ).
 Suy ra MD ME AE EC AC
 B M C
 Bài 4: Cho ABC cân tại A , lấy điểm D trên AB . Lấy điểm E trên tia đối của tia CA sao cho 
 CE BD . Kẻ DF //AC F BC .
 a) DBF là tam giác gì?
 b) Chứng minh tứ giác DCEF là hình bình hành.
 Trang 3 TÀI LIỆU CỦA NHÓM: CÁC DỰ ÁN GIÁO DỤC
 Lời giải
 a) Vì ABC cân ở A nên ·ABC ·ACB mà DF //AC nên B· FD ·ACB (hai góc đồng vị). 
 Do đó B· FD ·ABC suy ra DBF là tam giác cân tại D .
 b)Vì DBF là tam giác cân tại D nên DF BD mà CE BD do đó CE DF . A
 Mặt khác CE//DF (vì DF //AC )
 Vậy tứ giác DCEF là hình bình hành.
 D
TÀI LIỆU CỦA NHÓM: CÁC DỰ ÁN GIÁO DỤC
 C
 B F
 Bài 5: Cho ABC có các đường trung tuyến BE,CF và trọng tâm G . Gọi M , N lần lượt là trung E
 điểm của BG và CG .
 a) Chứng minh EF //MN và EF MN .
 b) Chứng minh MNEF là hình bình hành.
 Lời giải
 a) Vì ABC có BE,CF là các đường trung tuyến nên F , E lần lượt là trung điểm các cạnh AB , AC
 1
 nên FE là đường trung bình. Do đó FE//BC và FE BC . 1 
 2
 Vì M , N lần lượt là trung điểm của BG và CG nên MN là đường trung bình của GBC
 1
 Do đó MN//BC và MN BC . 2 
 2
 Từ 1 và 2 suy ra EF //MN và EF MN .
 b) Theo câu a) ta có EF //MN và EF MN do đó MNEF là hình bình hành.
 Bài 6: Cho hình bình hành ABCD. Kéo dài đường trung tuyến AM của ABC và lấy điểm E 
 sao cho ME MA .
 a) Tứ giác ABEC là hình gì? 
 b) Chứng minh D , C , E thẳng hàng và suy ra C là trung điểm của DE.
 Lời giải
 Trang 4 TÀI LIỆU CỦA NHÓM: CÁC DỰ ÁN GIÁO DỤC
 A D
 M
 B C
 E
TÀI LIỆU CỦA NHÓM: CÁC DỰ ÁN GIÁO DỤC a) Tứ giác ABEC có MA ME (gt) và MB MC ( AM là trung tuyến của ABC )
 Suy ra tứ giác ABEC là hình bình hành (hai đường chéo cắt nhau tại trung điểm của mỗi 
 đường)
 b) Ta có: ABEC là hình bình hành AB//CE và AB CE 1 
 Mặt khác ABCD là hình bình hành nên AB//CD và AB CD 2 
 Từ 1 và 2 suy ra D , C , E thẳng hàng và AB CE CD.
 Do đó D , C , E thẳng hàng và C là trung điểm của DE.
 Bài 7: Cho tứ giác ABCD có M , N , P , Q lần lượt là trung điểm của AB , BC , CD , DA .
 1
 a) Chứng minh MN //AC và MN AC.
 2
 b) Chứng minh MN //PQ và MN PQ.
 c) Chứng minh tứ giác MNPQ là hình bình hành.
 Lời giải
 A
 M
 B
 Q
 N
 D P C
 a) Ta có: M là trung điểm của BA và N là trung điểm BC
 Do đó MN là đường trung bình của tam giác BAC
 1
 MN //AC và MN AC. 1
 2 
 b) P là trung điểm DC và Q là trung điểm của DA
 Do đó PQ là đường trung bình của tam giác DAC
 1
 PQ//AC và PQ AC. 2
 2 
 Trang 5 TÀI LIỆU CỦA NHÓM: CÁC DỰ ÁN GIÁO DỤC
 Từ 1 và 2 suy ra MN //PQ //AC và MN PQ AC 
 c) Xét từ giác MNPQ có
 MN / / PQ cmt 
 MN PQ cmt
 Suy ra tứ giác MNPQ là hình bình hành (vì có cặp cạnh đối song song và bằng nhau)
 Bài 8: Cho hình bình hành ABCD. E và F lần lượt là hình chiếu của A và C trên đường chéo BD.
 a) Chứng minh ADE CBF .
 b) Chứng minh tứ giác AECF là hình bình hành.
 Lời giải
TÀI LIỆU CỦA NHÓM: CÁC DỰ ÁN GIÁO DỤC
 A B
 F
 E
 D C
 a) Ta có: ABCD hình bình hành AD//BC ·ADE C· BF (hai góc so le trong)
 Xét hai tam giác vuông ADE và CBF có
 A· ED C· FB 90
 AD BC ( ABCD là hình bình hành)
 ·ADE C· BF (cmt)
 Do đó ADE CBF (cạnh huyền – góc nhọn)
 b) Vì ADE CBF AE CF (cặp cạnh tương ứng)
 AE  BD
 AE//CF
 CF  BD
 Xét tứ giác AECF có:
 AE CF cmt 
 AE //CF cmt
 Tứ giác AECF là hình bình hành (vì có cặp cạnh đối song song và bằng nhau)
 Bài 9: Cho hình bình hành ABCD có AB AD . Vẽ AE  BD ,CF  BD , AE kéo dài cắt CD 
 tại H và CF kéo dài cắt AB tại K . Chứng minh:
 a) AECF là hình bình hành.
 b) AHCK là hình bình hành.
 Lời giải
 Trang 6 TÀI LIỆU CỦA NHÓM: CÁC DỰ ÁN GIÁO DỤC
 A K B
 F
 E
 D H C
 · ·
 a) Ta có: ABCD hình bình hành AD//BC ADE CBF (hai góc so le trong)
 Xét hai tam giác vuông ADE và CBF có
 A· ED C· FB 90
TÀI LIỆU CỦA NHÓM: CÁC DỰ ÁN GIÁO DỤC
 AD BC ( ABCD là hình bình hành)
 ·ADE C· BF (cmt)
 Do đó ADE CBF (cạnh huyền – góc nhọn)
 AE CF (cặp cạnh tương ứng)
 AE  BD
 AE//CF
 CF  BD
 Xét tứ giác AECF có:
 AE CF cmt 
 AE //CF cmt
 Tứ giác AECF là hình bình hành (vì có cặp cạnh đối song song và bằng nhau)
 b) Ta có: ABCD hình bình hành AB//CD hay AK //HC (vì K AB, H CD)
 Xét tứ giác AHCK có AK //HC (cmt) và AH //CK (vì AE//CF )
 Suy ra tứ giác AHCK là hình bình hành.
 Bài 10: Cho hình bình hành ABCD. Kẻ AE  BD và CF  BD.
 a) Tứ giác AECF là hình gì? Vì sao?
 b) AE cắt CD tại I , CF cắt AB tại K . Chứng minh AI CK .
 c) Chứng minh DE BF.
 Lời giải
 A K B
 F
 E
 D I C
 a) Ta có: ABCD hình bình hành AD//BC ·ADE C· BF (hai góc so le trong)
 Xét hai tam giác vuông ADE và CBF có
 Trang 7 TÀI LIỆU CỦA NHÓM: CÁC DỰ ÁN GIÁO DỤC
 A· ED C· FB 90
 AD BC ( ABCD là hình bình hành)
 ·ADE C· BF (cmt)
 Do đó ADE CBF (cạnh huyền – góc nhọn)
 AE CF (cặp cạnh tương ứng)
 AE  BD
 AE//CF
 CF  BD
 Xét tứ giác AECF có:
 AE CF cmt 
 AE //CF cmt
TÀI LIỆU CỦA NHÓM: CÁC DỰ ÁN GIÁO DỤC 
 Tứ giác AECF là hình bình hành (vì có cặp cạnh đối song song và bằng nhau)
 b) Ta có: ABCD hình bình hành AB//CD hay AK //HI (vì K AB , I CD)
 Xét tứ giác AICK có AK //IC (cmt) và AI //CK (vì AE //CF )
 Suy ra tứ giác AICK là hình bình hành.
 AI CK.
 c) Từ câu a) ta có ADE CBF DE BF (cặp cạnh tương ứng)
 Bài 11: Cho hình bình hành ABCD có AB CD . Tia phân giác góc Aˆ cắt BC ở I , tia phân giác 
 góc Cˆ cắt AD tại K . Chứng minh:
 a, ABI là tam giác cân.
 b, So sánh B· IA và K· CB .
 c, Tứ giác AICK là hình bình hành.
 Lời giải
 B I C
 A K D
 a) Vì tứ giác ABCD là hình bình hành AB / /CD ; AD / /BC
 ·BAD
 Vì AI là tia phân giác của B· AD B· AI I·AD 1 
 2
 Vì BC / / AD B· IA I·AD (so le trong) 2 
 Từ 1 và 2 B· IA B· AI ABI cân tại B .
 ·BCD
 b) Vì CK là tia phân giác của B· CD B· CK D· CK 3 
 2
 Vì tứ giác ABCD là hình bình hành B· AD B· CD 4 
 Từ 1 , 3 , 4 B· AI K· CB mà B· IA B· AI B· IA K· CB 
 Trang 8 TÀI LIỆU CỦA NHÓM: CÁC DỰ ÁN GIÁO DỤC
 c) Vì B· IA K· CB mà hai góc này ở vị trí đồng vị AI / /CK mà CI / / AK
 Tứ giác AICK là hình bình hành.
 Bài 12: Cho hình bình hành ABCD có M , N lần lượt là trung điểm của AB và CD . Nối AN và 
 CM cùng cắt BD lần lượt ở E và F . Chứng minh:
 a, AM CN và tứ giác AMCN là hình bình hành.
 b, F là trung điểm của BE và E là trung điểm của DF .
 Lời giải
 B C
 F
 M N
 E
TÀI LIỆU CỦA NHÓM: CÁC DỰ ÁN GIÁO DỤC
 A D
 a) Vì tứ giác ABCD là hình bình hành AB / /CD ; AD / /BC ; AB CD ; AD BC .
 AB CD
 Vì M , N lần lượt là trung điểm của AB và CD AM MB ; CN ND 
 2 2
 mà AB CD AM MB CN ND .
 Xét tứ giác AMCN có AM CN và AM / /CN Tứ giác AMCN là hình bình hành.
 b) Vì tứ giác AMCN là hình bình hành MC / / AN hay MF / / AE; NE / /CF .
 Xét ABE có: M là trung điểm của AB và MF / / AE F là trung điểm của BE .
 Xét CDF có: N là trung điểm của CD và NE / /CF E là trung điểm của F .
 Bài 13: Cho hình bình hành ABCD , Trên cạnh AB lấy điểm M , trên cạnh CD lấy điểm N sao cho 
 AM CN
 a, Chứng minh rằng: DM BN .
 b, Chứng minh tứ giác AMCN là hình bình hành.
 c, Chứng minh tứ giác BMDN là hình bình hành.
 Lời giải
 A M B
 D N C
 a) Vì tứ giác ABCD là hình bình hành AB / /CD; AD / /BC; AB CD; BC AD và 
 D· AM B· CN
 Xét ADM và CBN có: AD / /BC ; D· AM B· CN ; AM / /CN
 ADM CBN (c.g.c) DM BN .
 b) Xét tứ giác AMCN có AM / /CN và AM / /CN Tứ giác AMCN là hình bình hành 
 c) Ta có AB CD và AM CN AB AM CD CN BM DN
 Trang 9 TÀI LIỆU CỦA NHÓM: CÁC DỰ ÁN GIÁO DỤC
 Xét tứ giác BMDN có BM DN và BM / /DN 
 Tứ giác BMDN là hình bình hành DM BN .
 Bài 14: Cho hình bình hành ABCD , trên cạnh AB lấy điểm E , trên cạnh CD lấy điểm F sao cho 
 AE CF. Gọi O là giao điểm của AC và BD .
 a, Chứng minh tứ giác AECF là hình bình hành.
 b, Chứng minh O là trung điểm của EF .
 Lời giải
 A E B
 O
TÀI LIỆU CỦA NHÓM: CÁC DỰ ÁN GIÁO DỤC
 D F C
 a) Vì tứ giác ABCD là hình bình hành AB / /CD ; AD / /BC ; AB CD ; BC AD
 Xét tứ giác AECF có AE CF và AE / /CF Tứ giác AECF là hình bình hành 
 b) Vì tứ giác ABCD là hình bình hành có AC cắt BD tại O O là trung điểm của AC .
 Vì tứ giác AECF là hình bình hành EF cắt AC tại trung điểm của mỗi đường
 Mà O là trung điểm của AC O là trung điểm của EF .
 Bài 15: Cho hình bình hành ABCD . Gọi H và K lần lượt là hình chiếu của A và C trên đường 
 chéo BD.
 a, Chứng minh rằng: DH BK .
 b, Chứng minh rằng tứ giác AHCK là hình bình hành.
 c, Gọi O là trung điểm của HK . Chứng minh rằng ba điểm A, O , C thẳng hàng.
 Lời giải
 A B
 K
 O
 H
 D C
 a) Vì tứ giác ABCD là hình bình hành AB / /CD ; AD / /BC ; AB CD ; BC AD
 Vì H và K lần lượt là hình chiếu của A và C trên đường chéo BD AH  BD;CK  BD 
 AHD vuông tại H và CKB vuông tại K .
 Vì AD / /BC ·ADH C· BK (so le trong).
 Xét AHD và CKB có: ·AHD C· KB 90 ; AD BC ; ·ADH C· BK
 AHD CKB (cạnh huyền – góc nhọn) DH BK .
 b) Vì AHD CKB (chứng minh trên) AH CK .
 Vì AH  BD và CK  BD AH / /CK .
 Xét tứ giác AHCK có AH / /CK và AH CK Tứ giác AHCK là hình bình hành.
 Trang 10