Đề thi minh họa kì thi Trung học Phổ thông Quốc gia năm 2017 môn Toán học
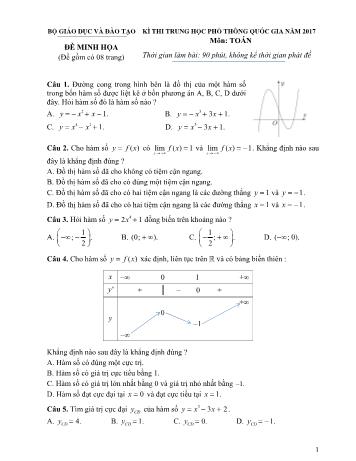
Câu 1. Đường cong trong hình bên là đồ thị của một hàm số
trong bốn hàm số được liệt kê ở bốn phương án A, B, C, D dưới
đây. Hỏi hàm số đó là hàm số nào ?
A. y x2 x 1. B. y x3 3x 1.
C. y x4 x2 1. D. y x3 3x 1.
Câu 2. Cho hàm số y f (x) có lim ( ) 1
Khẳng định nào sau
đây là khẳng định đúng ?
A. Đồ thị hàm số đã cho không có tiệm cận ngang.
B. Đồ thị hàm số đã cho có đúng một tiệm cận ngang.
C. Đồ thị hàm số đã cho có hai tiệm cận ngang là các đường thẳng y 1 và y 1.
D. Đồ thị hàm số đã cho có hai tiệm cận ngang là các đường thẳng x 1 và x 1.
Câu 3. Hỏi hàm số y 2x4 1 đồng biến trên khoảng nào ?
Câu 4. Cho hàm số y f (x) xác định, liên tục trên và có bảng biến thiên :
x 0 1 +
Khẳng định nào sau đây là khẳng định đúng ?
A. Hàm số có đúng một cực trị.
B. Hàm số có giá trị cực tiểu bằng 1.
C. Hàm số có giá trị lớn nhất bằng 0 và giá trị nhỏ nhất bằng 1.
D. Hàm số đạt cực đại tại x 0 và đạt cực tiểu tại x 1.
Câu 5. Tìm giá trị cực đại yCĐ của hàm số y x3 3x 2.
Tóm tắt nội dung tài liệu: Đề thi minh họa kì thi Trung học Phổ thông Quốc gia năm 2017 môn Toán học
1 BỘ GIÁO DỤC VÀ ĐÀO TẠO ĐỀ MINH HỌA (Đề gồm có 08 trang) KÌ THI TRUNG HỌC PHỔ THÔNG QUỐC GIA NĂM 2017 Môn: TOÁN Thời gian làm bài: 90 phút, không kể thời gian phát đề Câu 1. Đường cong trong hình bên là đồ thị của một hàm số trong bốn hàm số được liệt kê ở bốn phương án A, B, C, D dưới đây. Hỏi hàm số đó là hàm số nào ? A. 2 1.y x x B. 3 3 1.y x x C. 4 2 1.y x x D. 3 3 1.y x x Câu 2. Cho hàm số ( )y f x có lim ( ) 1 x f x và lim ( ) 1 x f x . Khẳng định nào sau đây là khẳng định đúng ? A. Đồ thị hàm số đã cho không có tiệm cận ngang. B. Đồ thị hàm số đã cho có đúng một tiệm cận ngang. C. Đồ thị hàm số đã cho có hai tiệm cận ngang là các đường thẳng 1y và 1y . D. Đồ thị hàm số đã cho có hai tiệm cận ngang là các đường thẳng 1x và 1x . Câu 3. Hỏi hàm số 42 1y x đồng biến trên khoảng nào ? A. 1 ; 2 . B. (0; ). C. 1 ; 2 . D. ( ; 0). Câu 4. Cho hàm số ( )y f x xác định, liên tục trên và có bảng biến thiên : x 0 1 + 'y + 0 + ...] . C. D ( ; 1) (3; ). D. D ( 1; 3) . Câu 16. Cho hàm số 2 ( ) 2 .7 .x xf x Khẳng định nào sau đây là khẳng định sai ? A. 2 2( ) 1 log 7 0.f x x x B. 2( ) 1 ln 2 ln 7 0.f x x x C. 27( ) 1 log 2 0.f x x x D. 2( ) 1 1 log 7 0.f x x Câu 17. Cho các số thực dương a, b, với a 1. Khẳng định nào sau đây là khẳng định đúng ? A. 2 1 log ( ) log . 2 aa ab b B. 2log ( ) 2 2log .aa ab b C. 2 1 log ( ) log . 4 aa ab b D. 2 1 1 log ( ) log . 2 2 aa ab b Câu 18. Tính đạo hàm của hàm số 1 4x x y . A. 2 1 2( 1)ln 2 ' 2 x x y . B. 2 1 2( 1)ln 2 ' 2 x x y . C. 2 1 2( 1)ln 2 ' 2x x y . D. 2 1 2( 1)ln 2 ' 2x x y . Câu 19. Đặt 2log 3a , 5log 3b . Hãy biểu diễn 6log 45 theo a và b. A. 6 2 log 45 . a ab ab B. 2 6 2 2 log 45 . a ab ab C. 6 2 log 45 . a ab ab b D. 2 6 2 2 log 45 . a ab ab b Câu 20. Cho hai số thực a và b, với 1 a b . Khẳng định nào dưới đây là khẳng định đúng ? A. log 1 loga bb a . B. 1 log loga bb a . C. log log 1b aa b . D. log 1 logb aa b . 4 Câu 21. Ông A vay ngắn hạn ngân hàng 100 triệu đồng, với lãi suất 12%/năm. Ông muốn hoàn nợ cho ngân hàng theo cách : Sau đúng một tháng kể từ ngày vay, ông bắt đầu hoàn nợ; hai lần hoàn nợ liên tiếp cách nhau đúng một tháng, số tiền hoàn nợ ở mỗi lần là như nhau và trả hết tiền nợ sau đúng 3 tháng kể từ ngày vay. Hỏi, theo cách đó, số tiền m mà ông A sẽ phải trả cho ngân hàng trong mỗi lần hoàn nợ là bao nhiêu ? Biết rằng, lãi suất ngân hàng không thay đổi trong thời gian ông A hoàn nợ. A. 3100.(1,01) 3 m (triệu đồng). B. 3 3 (1,01) (1,01) 1 m (triệu đồng). C. 100 1,03 3 m (triệu đồng). D. 3 3 120.(1,12) (1,12) 1 m (triệu đồng). Câu 22. Viết công thức tính thể tích V của khối tròn xoay được tạo ra khi quay hình thang cong, giới hạn bởi đồ thị hàm số y f(x), trục Ox và hai đường thẳng x a, x b (a b), xung quanh trục Ox. A. 2 ( )d b a V f x x . B. 2 ( )d ...z . Tính tổng 1 2 3 4| | | | | | | |T z z z z . A. T 4. B. 2 3.T C. 4 2 3.T D. 2 2 3.T Câu 34. Cho các số phức z thỏa mãn | z | 4. Biết rằng tập hợp các điểm biểu diễn các số phức (3 4 )w i z i là một đường tròn. Tính bán kính r của đường tròn đó. A. r 4. B. r 5. C. r 20. D. r 22. Câu 35. Tính thể tích V của khối lập phương . ' ' ' 'ABCD A B C D , biết ' 3AC a . A. 3V a . B. 33 6 . 4 a V C. 33 3 .V a D. 3 1 . 3 V a Câu 36. Cho hình chóp tứ giác S.ABCD có đáy ABCD là hình vuông cạnh a, cạnh bên SA vuông góc với mặt phẳng đáy và 2SA a . Tính thể tích V của khối chóp S.ABCD. 6 A. 32 . 6 a V B. 32 . 4 a V C. 32 .V a D. 32 . 3 a V Câu 37. Cho tứ diện ABCD có các cạnh AB, AC và AD đôi một vuông góc với nhau; AB 6a, AC 7a và AD 4a. Gọi M, N, P tương ứng là trung điểm các cạnh BC, CD, DB. Tính thể tích V của tứ diện AMNP. A. 3 7 . 2 V a B. 314 .V a C. 3 28 . 3 V a D. 37 .V a Câu 38. Cho hình chóp tứ giác S.ABCD có đáy là hình vuông cạnh bằng 2a . Tam giác SAD cân tại S và mặt bên (SAD) vuông góc với mặt phẳng đáy. Biết thể tích khối chóp S.ABCD bằng 3 4 . 3 a Tính khoảng cách h từ B đến mặt phẳng (SCD). A. 2 . 3 h a B. 4 . 3 h a C. 8 . 3 h a D. 3 . 4 h a Câu 39. Trong không gian, cho tam giác ABC vuông tại A, AB a và 3 .AC a Tính độ dài đường sinh l của hình nón, nhận được khi quay tam giác ABC xung quanh trục AB. A. l a. B. 2l a . C. 3l a . D. l 2a. Câu 40. Từ một tấm tôn hình chữ nhật kích thước 50cm 240cm, người ta làm các thùng đựng nước hình trụ có chiều cao bằng 50cm, theo hai cách sau (xem hình minh họa dưới đây) : Cách 1 : Gò tấm tôn ban đầu thành mặt xung quanh của thùng. Cách 2 : Cắt tấm tôn ban đầu thành hai tấm bằng nhau, rồi gò mỗi tấm đó thành mặt xung quanh của một thùng. Kí hiệu 1V là thể tích của thùng gò được theo cách 1 và 2V là tổng thể tích của hai thùng gò được theo cách 2. Tính tỉ số 1 2 V V . A. 1 2 1 2 V V . B. 1 2
File đính kèm:
 de_thi_minh_hoa_ki_thi_trung_hoc_pho_thong_quoc_gia_nam_2017.pdf
de_thi_minh_hoa_ki_thi_trung_hoc_pho_thong_quoc_gia_nam_2017.pdf

