Đề minh họa thi tốt nghiệp THPT môn Toán Lớp 12 - Chuyên đề: Ứng dụng tích phân - Năm học 2020-2021 (Có đáp án)

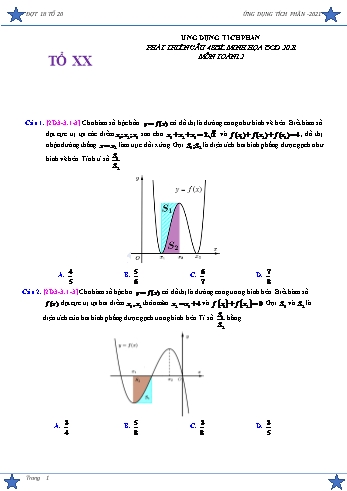
 ĐỢT 18 TỔ 20 ỨNG DỤNG TÍCH PHÂN -2021 
 ỨNG DỤNG TÍCH PHÂN
 PHÁT TRIỂN CÂU 48 ĐỀ MINH HỌA BGD 2021
 TỔ XX MÔN TOÁN12
 Câu 1. [2D3-3.1-3] Cho hàm số bậc bốn y f (x) có đồ thị là đường cong như hình vẽ bên. Biết hàm số 
 đạt cực trị tại các điểm x1; x2 ; x3 sao cho x1 x2 x3 2 2 và f (x1) f (x2 ) f (x3 ) 4 , đồ thị 
 nhận đường thẳng x x2 làm trục đối xứng. Gọi S1;S2 là diện tích hai hình phẳng được gạch như 
 S
 hình vẽ bên. Tính tỉ số 1
 S2
 4 5 6 7
 A. . B. . C. . D. .
 5 6 7 8
Câu 2. [2D3-3.1-3] Cho hàm số bậc ba y f (x) có đồ thị là đường cong trong hình bên. Biết hàm số 
 f (x) đạt cực trị tại hai điểm x1, x2 thỏa mãn x2 x1 4 và f x1 f x2 0 . Gọi S1 và S2 là 
 S
 diện tích của hai hình phẳng được gạch trong hình bên. Tỉ số 1 bằng
 S2
 3 5 3 3
 A. . B. . C. . D. .
 4 8 8 5
 Trang 1 ĐỢT 18 TỔ 20 ỨNG DỤNG TÍCH PHÂN -2021 
Câu 3. [2D3-3.1-3] Cho hàm số y f (x) ax4 bx2 c có đồ thị C , Biết f ( 1) 0 . Tiếp tuyến 
 d tại điểm có hoành độ x 1 của C cắt C tại 2 điểm có hoành độ lần lượt là 0 và 2, Gọi 
 S1
 S1;S2 là diện tích hình phẳng (phần gạch chéo trong hình vẽ). Tính tỷ số 
 S2
 1 1 1 2
 A. B. C. D. 
 5 14 28 25
 3 2
Câu 4. [2D3-3.1-3] Cho hai hàm số y f (x) và y g '(x) , f x ax bx cx 2 và g(0) 2 (có 
 đồ thị như hình vẽ dưới đây). Tính diện tích hình phẳng giới hạn bởi hai đồ thị y f (x) và 
 3 5
 y g(x) , biết rằng g(x) f (x)dx .
 2 12
 37 162 37 9
 A. .S B. . S C. . D. . S S 
 6 35 12 4
 Trang 2 ĐỢT 18 TỔ 20 ỨNG DỤNG TÍCH PHÂN -2021 
Câu 5. [2D3-3.1-3] Cho hàm số bậc ba y f x và hàm bậc hai y g x có đồ thị là hai đường 
 cong như hình vẽ bên. Biết hàm số f x đạt cực trị tại hai điểm x1, x2 thỏa mãn:x1 x2 1 và 
 f x1 f x2 0. Gọi S1 và S2 là diện tích của hai hình phẳng được gạch trong hình bên. Tỉ 
 S
 số 1 thuộc khoảng nào sau
 S2
 3 3 7 7 5 
 A. 1; B. ; C. ;2 D. 2; 
 2 2 4 4 2 
Câu 6. [1D3-2.2-3] Cho hàm số bậc bốn y f x có đồ thị là đường cong (C) như hình bên. Biết 
 3
 hàm số y f x có 3 điểm cực trị lập thành cấp số cộng có công sai d thỏa mãn 
 2
 x1 x3 1và cắt trục tung tại điểm có tung độ bằng 1 .Gọi S 1 và S2 ,S3 là diện tích của các 
 S
 hình phẳng được gạch trong hình bên. Tính tỉ số 1 .
 S2 S3
 Trang 3 ĐỢT 18 TỔ 20 ỨNG DỤNG TÍCH PHÂN -2021 
 A. 2. B. 3. C. 5. D. 4.
Câu 7. [2D3-3.1-3] Cho parabol (P) : y = f (x)= x2 và đường thẳng (d) : y ax b có đồ thị như hình 
 vẽ bên. Biết parabol (P) và đường thẳng (d)cắt nhau tại hai điểm phân biệt có hoành độ x1, x2 
 thỏa mãn x1 = x2 - 3 và f (x1 ) + f (x2 ) = 5 . Gọi S1 và S2 là diện tích của hai hình phẳng được 
 gạch trong hình. Tính S1 + S2 .
 8 5 7
 A. .3 B. .C. . D. .
 3 3 3
Câu 8. [2D3-3.1-4] Cho hàm số bậc bốn y f x có đồ thị là đường cong trong hình bên. Biết hàm số 
 y f x có 3 điểm cực trị là x1, x2 , x3 thỏa mãn x3 x1 4 và f x2 4 , đồ thị nhận đường 
 thẳng x x2 làm trục đối xứng. Gọi S1 và S2 là diện tích của hai hình phẳng được gạch như trong 
 S
 hình vẽ . Tỉ số 1 bằng
 S2
 7 6 9 8
 A. . B. . C. . D. .
 6 7 7 7
Câu 9 . [2D3-3.1-4] Cho hàm số y f x có đồ thị C nằm phía trên trục hoành. Hàm số y f x
 2 1 
 thỏa mãn các điều kiện f x f x . f x 4 0 , f 0 0, f 3 . Tính diện tích 
 2 
 S là hình phẳng giới hạn bởi C và trục hoành. 
 A. . B. . C. . D. . 2 
 4 2
 Trang 4 ĐỢT 18 TỔ 20 ỨNG DỤNG TÍCH PHÂN -2021 
Câu 10. [2D3-3.1-3] Cho hàm số y = f (x) có đồ thị là đường cong trong hình vẽ, với f (x) là hàm số 
 bậc ba. Biết hàm số f (x) đạt cực trị tại điểm x1;x2 thỏa mãn x2 = x1 + 2 và 
 f (x1)+ f (x2 ) = 0 . Gọi S1,S2 là diện tích của hai hình phẳng được tô trong hình vẽ dưới đây. 
 S
 Tỷ số 1 bằng
 S2
 3 5 5 5
 A. . B. . C. . D. . 
 5 11 13 21
Câu 11. [2D3-3.1-4] Cho hàm số bậc bốn y f (x) có đồ thị là đường cong trong hình. Biết hàm số 
 y f (x) đạt cực trị tại ba điểm x1; x2 ; x3 thỏa mãn x1 3 x2 x3 1 . Gọi S là1 diện tích của 
 hình phẳng được tô đậm và S2 là diện tích của hình phẳng được gạch chéo trong hình bên. Tỉ 
 S
 số 1 bằng
 S2
 891 297 17 227
 A. . B. . C. . D. .
 17 20 60 15
Câu 12. [2D3-3.1-4] Cho hàm số y f x là hàm số bậc 4 và có đồ thị như hình vẽ. Biết hàm số 
 f x đạt cực trị tại các điểm x1, x2, x 3và x1, x2, x theo3 thứ tự lập thành một cấp số cộng có 
 công sai bằng 2; 9 f x2 7 f x3 0 . Gọi S1,S2 lần lượt là diện tích của hai hình phẳng được 
 S
 gạch trong hình vẽ. Tỉ số 1 bằng 
 S2
 Trang 5 ĐỢT 18 TỔ 20 ỨNG DỤNG TÍCH PHÂN -2021 
 17 23 68 41
 A. . B. . C. . D. .
 15 17 37 35
Câu 13. [2D3-3.1-4] Cho hàm số bậc bốn y f x có đồ thị là đường cong như hình vẽ bên. Biết hàm 
 số đạt cực trị tại các điểm x1, x2, x 3theo thứ tự lập thành cấp số cộng có công sai bằng 1 và 
 f x1 f x3 , gọi S1, S2 là diện tích hai hình phẳng được gạch trong hình bên. Tính tỷ số 
 S
 1 .
 S2
 7 6 7 7
 A. . B. . C. . D. .
 15 15 8 16
 ax + b
Câu 14 . [2H3-3.1-3] Cho hàm số y = (a.c ¹ 0) có đồ thị là đường cong (C) như hình vẽ
 cx + d
 Trang 6 ĐỢT 18 TỔ 20 ỨNG DỤNG TÍCH PHÂN -2021 
 Gọi D là tiếp tuyến của (C) tại điểm có hoành độ x = - 1 và (C ') là đồ thị hàm số 
 ax + b
 y = . Đặt S là diện tích hình phẳng giới hạn bởi (C ') và hai trục Ox,Oy . Đặt S là diện 
 cx + d 1 2
 S
 tích hình phẳng giới hạn bởi (C ') , D và y = 1 . Gọi k = 2 , giá trị của k thuộc khoảng nào sau 
 S1
 đây?
 A. .( 4;5) B. . (1;3) C. . (3;D.4) . (1;2)
Câu 15. [2D3-3.2-3] Cho đồ thị hàm bậc bốn y f x như hình vẽ minh họa bên dưới. Biết hàm số đạt 
 cực trị lần lượt tại ba điểm x1, x2 , x 3thỏa mãn x3 x1 4 và f x2 ,1 đồ thị đối xứng qua 
 đường thẳng x x2 . Gọi S1 và S2 là diện tích của hình phẳng được xác định như trong hình. 
 24S
 Tính tỉ số 1 .
 S2
 21 24
 A. .2 4 B. . C. . D. . 21
 8 15
Câu 16. [2D3-3.1-4] Cho hàm số y f (x) ax4 bx2 c có đồ thị như hình vẽ. Biết y f (x) đạt cực 
 trị tại x1 x2 x3 , sao cho x1, x2 , x3 lập thành cấp số cộng với công sai bằng 2 và 
 S1
 f (x1) f (x3 ) 2 f (x2 ) . Gọi S1, S2 là diện tích phần gạch chéo trong hình. Tính 
 S2
 Trang 7 ĐỢT 18 TỔ 20 ỨNG DỤNG TÍCH PHÂN -2021 
 112 112 128
 A. . B. . C. . 16k D. .
 118 15 15
Câu 17. [2D3-3.1-3] Cho hàm số bậc ba f x có đồ thị hàm số như hình vẽ bên. Biết hàm số f x đạt 
 cực trị tại hai điểm x1, x2 thỏa mãn x2 x1 2 và f x1 f x2 1 . Gọi S1, S2 là diện tích của 
 S
 hai hình phẳng được gạch trong hình vẽ bên. Tính tỉ số 1 . 
 S2
 5 3 3 5
 A. . B. . C. . D. .
 4 5 8 8
Câu 18. [1D3-2.1-2] Cho hàm số bậc bốn có đồ thị y f x như hình vẽ bên. Biết hàm số đạt cực trị 
 tại ba điểm x1, x2 , x3 như hình vẽ thỏa mãn x3 x2 1 và f x2 4 , đồ thị nhận đường thẳng 
 x x2 làm trục đối xứng. Gọi S1,S 2là diện tích của hình phẳng được gạch như trong hình. 
 S
 Tính tỉ số 1 bằng
 S2
 1 3 7
 A. .1 B. . C. . D. .
 2 7 8
 Trang 8 ĐỢT 18 TỔ 20 ỨNG DỤNG TÍCH PHÂN -2021 
 1
Câu 19. [2D3-3.2-3] Cho hàm số y x3 bx2 3 có đồ thì C . Đường thẳng y 1 là tiếp tuyến tại 
 2
 điểm cực tiểu có hoành độ x2 của đồ thị C đồng thời cắt đồ thị C tại điểm có hoành độ x1 . 
 S1
 Tính tỷ số diện tích với S1, S2 được thể hiện trong hình vẽ.
 S2
 27 24 9
 A. .1 B. . C. . D. .
 51 51 8
Câu 20. [2D3-5.7-3] Cho hàm số bậc bốn y f x có đồ thị là đường cong như hình vẽ. Biết hàm số 
 f x có ba điểm cực trị x1, x2 , x3 và ba điểm cực trị này tạo thành một cấp số cộng có công sai 
 bằng 2 thỏa mãn f x3 4 .Đồ thị hàm số nhận đường thẳng x x2 làm trục đối xứng, gọi S1, S2 
 S
 là diện tích của hai hình phẳng được gạch trong hình bên. Tỉ số 1 bằng
 S2
 47 8 7 28
 A. . B. . C. . D. .
 28 7 8 47
Câu 21. [2D3-3.2-3] Cho hàm số bậc ba y f x x3 bx2 cx d có đồ thị như hình vẽ. 
 S1
 f x1 2,5 x1 . Xác định tỉ lệ .
 S2
 Trang 9 ĐỢT 18 TỔ 20 ỨNG DỤNG TÍCH PHÂN -2021 
 8 2 16 8
 A. . B. . C. . D. .
 27 27 27 27
 3
Câu 22. [2D3-3.2-3] Cho hàm số y f (x) x 3x 1và điểm M (x0 ; y0 ) thuộc đồ thị của hàm số 
 y f (x) như hình vẽ. Đường thẳng OM cắt đồ thị tại 3 điểm có hoành độ x0 , x1, x2 thỏa mãn 
 2 S1
 x0 1 0 x1 x2 và x1 x0 x1 x1x2 1 . Tỷ số diện tích nằm trong khoảng nào dưới 
 S2
 đây 
 A. . 1;2 B. . 2;3 C. . 3;4 D. . 4;5 
Câu 23. [2D3-3.2-3] Cho hàm số bậc ba y f (x) có đồ thị là đường cong trong hình dưới. Biết hàm số 
 f (x) đạt cực trị tại hai điểm x1, x2 thỏa mãn x2 x1 4 và f x1 f x2 2k . Gọi S1 và S2 
 là diện tích của hai hình phẳng được cho trong hình dưới. 
 Trang 10