Đề cương ôn tập môn Hình học Lớp 8 - Bài 3: Tính chất đường phân giác của tam giác

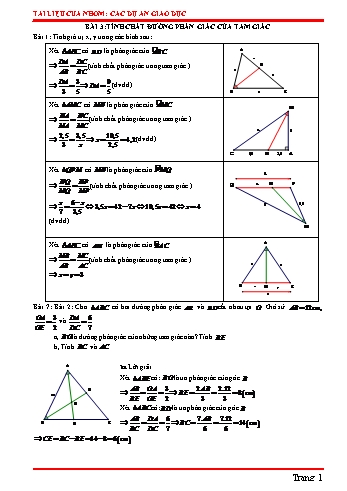
 TÀI LIỆU CỦA NHÓM: CÁC DỰ ÁN GIÁO DỤC
 BÀI 3:TÍNH CHẤT ĐƯỜNG PHÂN GIÁC CỦA TAM GIÁC 
Bài 1: Tình giá trị x, y trong các hình sau:
 Xét ABC có BD là phân giác của ·ABC A
 x
 DA DC D
 (tính chất phân giác trong tam giác ) 3
 AB BC 3
 DA 3 9
 DA (đvđd)
 3 5 5 B 5 C
 ·
 Xét AMC có MN là phân giác của AMC M
 NA NC
 (tính chất phân giác trong tam giác )
 MA MC
 x 3
 2,5 3,5 10,5
 x 4,2 (đvđd)
 3 x 2,5
 C 3,5 N 2,5 A
 Xét QPM có MN là phân giác của P· MQ
 6
 NQ NP
 (tính chất phân giác trong tam giác ) Q x N P
 MQ MP
 x 6 x
 3,5x 42 7x 10,5x 42 x 4 7 3,5
 7 3,5
 (đvđd)
 M
 Xét ABC có AM là phân giác của B· AC A
 MB MC
 (tính chất phân giác trong tam giác )
 AB AC 5 5
 x y 3
 B x M y C
 6
Bài 7: Bài 2: Cho ABC có hai đường phân giác AE và BD cắt nhau tại O . Giả sử AB 12cm, 
OA 3 DA 6
 và . 
OE 2 DC 7
 a, BO là đường phân giác của những tam giác nào? Tính BE .
 b, Tính BC và AC .
 A  Lời giải
 Xét ABE có: BO là tia phân giác của góc B 
 D AB OA 3 2.AB 2.12
 12 BE 8 cm 
 BE OE 2 3 3
 O
 Xét ABC có: BD là tia phân giác của góc B
 AB DA 6 7.AB 7.12
 B E C BC 14 cm 
 BC DC 7 6 6
 CE BC BE 14 8 6 cm 
 Trang 1 TÀI LIỆU CỦA NHÓM: CÁC DỰ ÁN GIÁO DỤC
 AC EC 6 6.AB 6.12
Xét ABC có: AE là tia phân giác của góc A AC 9 cm 
 AB EB 8 8 8
Bài 3: Cho ABC có AB 3cm, AC 5cm , Đường phân giác AD cắt đường trung tuyến CM ở I.
 IC CD
 a, Tính . b, Tính .
 IM CB
  Lời giải
 Xét AMC có: AI là tia phân giác của góc A
 AM IM IC AC AC 2.AC 2.5 10
 B 2
 AC IC IM AM AB AB 3 5
 2
 D Xét ABC có: AD là tia phân giác của góc A
 M
 I AC DC 5 5
 DC DB
 AB DB 3 3
 5 8
 Mà BC BD DC BD DB DB
 A C 3 3
 5
 BD
 CD 5
 3 
 8
 CB DB 8
 3
Bài 4:Cho ABC vuông tại A , biết AB 6, AC 8 , Đường cao AH , phân giác BD . Gọi I là giao 
điểm của AH và BD .
 a, Tính AD, DC.
 IH AD
 b, Chứng minh .
 IA DC
 c, Chứng minh AB.BI BD.HB và AID cân.
  Lời giải
 a. Xét ABC vuông tại A có: 
 BC 2 AB2 AC 2 (định lý Pytago)
 A
 BC AB2 AC 2 62 82 10
 D Xét ABC có BD là tia phân giác góc B
 BA DA BA DA
 I 
 BC DC BC BA DC DA
 B C 6 DA DA 6 6.8
 H DA 3
 10 6 DC DA AC 16 16
 DC AC DA 8 3 5
 1 1 AB.AC 6.8
 b. S AH.BC AB.AC AH 4,8
 ABC 2 2 BC 10
 Xét ABH vuông tại H có: BA2 AH 2 HB2 (định lý Pytago)
 HB AB2 AH 2 62 4,82 3,6
 BA IA BH IH 3,6 3
 Xét ABH có BI là tia phân giác góc B hay 
 BH IH BA IA 6 5
 Trang 2 TÀI LIỆU CỦA NHÓM: CÁC DỰ ÁN GIÁO DỤC
 AD 3 AD IH 3 
 Mà 
 DC 5 DC IA 5 
 c. Xét ABD vuông tại A và HBI vuông tại H có: ·ABD H· BI ( BD là tia phân giác của Bµ )
 AB BD
 ABD # H BI (g.g) AB.BI BD.HB
 HB BI
 Ta có: ·AID H· IB (đối đỉnh) mà H· IB ·ADB (vì ABD # H BI)
 ·AID I·DA AID cân tại A .
Bài 5: Cho ABC , trung tuyến AD . Đường phân giác ·ADB cắt cạnh AB ở M . Đường phân giác 
của ·ADC cắt AC ở N Gọi K là giao điểm của AD và MN.
 MA DA
 a, So sánh và .
 MB DB
 b, Chứng minh rằng MN song song với BC.
 A
 c, Chứng minh AM.AC AN.AB
 d, Chứng minh K là trung điểm của MN.
 Lời giải M K N
 a. Xét ADB có: DM là tia phân giác ·ADB
 DA MA
 (t/c đường phân giác của tam giác) B D C
 DB MB
 b. Xét ADC có: DN là tia phân giác ·ADC
 DA NA
 (t/c đường phân giác của tam giác)
 DC NC
 Mà DB DC ( AD là đường trung tuyến của ABC )
 MA NA
 NM // BC (định lý talet đảo)
 MB NC
 AM AN
 c. Ta có: (cmt) AM.AC AN.AB
 AB AC
 d. Ta có: MM // BC N· MD M· DB (slt) mà B· DM M· DK ( DM là tia phân giác ·ADB )
 N· MD K· DM KMD cân tại K KM KD 1 
 Ta có: MM // BC M· ND N· DC (slt) mà C· DN N· DK ( DN là tia phân giác ·ADC )
 M· ND K· DN KND cân tại K KN KD 2 
 Từ 1 và 2 KM KN mà K MN K là trung điểm của MN.
Bài 6: Cho ABC có đường trung tuyến AM và MD là đường phân 
 A
giác trong MAB . Từ D kẻ đường thẳng song song với BC cắt AC
tại E.
 EA MA
 a, Chứng minh .
 EC MB D E
 b, Chứng minh: ME là đường phân giác của MAC .
 Lời giải
 B C
 a. Xét AMB có: MD là tia phân giác ·AMB M
 Trang 3 TÀI LIỆU CỦA NHÓM: CÁC DỰ ÁN GIÁO DỤC
 MA DA
 (t/c đường phân giác của tam giác) 1 
 MB DB
 Mặt khác, ta có: DE // BC (gt) 
 AD AE
 (định lý Talet) 2 
 DB EC
 MA AE
 Từ 1 và 2 
 MB EC
 b. Kẻ ME ' là tia phân giác của ·AMC .
 MA AE MA AE
 Ta có: mà MB MC ( AM là đường trung tuyến) 
 MB EC MC EC
 MA E ' A MA AE
 Xét AMC có ME ' là tia phân giác của ·AMC mà (cmt)
 MC E 'C MC EC
 E ' A EA E ' A EA E ' A EA
 E ' A EA
 E 'C EC E 'C E ' A EA EC AC AC
 E '  E ME là tia phân giác của ·AMC hay ME là đường phân giác của MAC .
Bài 7. Cho ABC có AM là trung tuyến. Gọi MD và ME lần lượt là phân giác trong các ΔAMB và 
 AMC .
 a) Chứng minh DE / /BC .
 DA DA
 b) Đặt BC a, AM b . Tính , và DE theo a và b .
 DB BA
 c) Tìm điều kiện của ABC để DE là đường trung bình của ABC .
 A
 I
 D E
 C
 B M
 Lời giải
 a) Vì MD là phân giác trong của AMB (gt)
 AM DA
 1 (tính chất đường phân giác của tam giác).
 BM DB
 Vì ME là phân giác trong của AMC (gt)
 AM EA
 2 (tính chất đường phân giác của tam giác).
 CM EC
 Mà MB MC 3 (Vì AM là đường trung tuyến).
 DA EA
 Từ 1 , 2 , 3 
 DB EC
 BC a
 b) Ta có: BC a, AM b MB MC 
 2 2
 DA AM DA b 2b DA EA EA 2b
 Lại có (câu a) ; Mà (câu a) 
 DB BM DB a a DB EC EC a
 2
 Gọi I là giao điểm của DE và AM .
 Trang 4 TÀI LIỆU CỦA NHÓM: CÁC DỰ ÁN GIÁO DỤC
 x
 m 
 AD DE AI x 2am
 Vì DE / /BC . Đặt DE x thì 2 x 
 AB BC AM a m a 2m
 2am
 AD DE AD 2m
 Từ a 2m 
 AB BC AB a a 2m
 c) DE là đường trung bình của ABC AD DB MA MB ABC vuông tại A . 
 FA DB EC
Bài 8: Cho ABC với ba đường phân giác AD, BE,CF . Chứng minh rằng:   1.
 FB DC EC
 A
 E
 F
 B D C
 Lời giải
 Vì AD, BE,CF là ba đường phân giác của ABC nên theo tính chất đường phân giác của 
 tam giác, ta có:
 FA AC DB AB EC BC
 1 2 3 
 FB BC DC AC EA AB
 Nhân các vế tương ứng của các đẳng thức 1 , 2 và 3 ta có:
 FA DB EC AC AB BC FA DB EC
       1 (đpcm)
 FB DC EC BC AC AB FB DC EC
Bài 9: Cho ABC , đường phân giác AD . Gọi E là điểm đối xứng với A qua C . Đường thẳng đi qua 
B và song song với AC cắt ED ở K . Chứng minh rằng D· AK 90o
 x
 K
 A
 B
 D C
 E
 Lời giải
 Vẽ Ax là tia đối của tia AC .
 BK DB
 Vì BK //AC nên 1 (Theo định lí Talet)
 CE DC
 DB AB
 Vì AD là đường phân giác của ABC nên 2 (tính chất đường phân giác)
 DC AC
 BK AB
 Từ 1 và 2 mà CE AC gt BK AB ABK cân tại B .
 CE AC
 B· KA B· AK (tính chất tam giác cân)
 Mà B· KA K· Ax (hai góc so le trong)
 AK là đường phân giác của B· Ax
 Do AD và AK là hai đường phân giác trong và ngoài của µA nên AK  AD (đpcm) 
 Trang 5 TÀI LIỆU CỦA NHÓM: CÁC DỰ ÁN GIÁO DỤC
Bài 10: Cho ABC có AB 16, BC 21,CA 32 . Đường phân giác trong và ngoài của µA cắt BC lần 
lượt tại D và E .
 a) Chứng minh B là trung điểm của EC .
 b) Tính DE . A
 E B D C
 Lời giải
 a) Vì đường phân giác trong và ngoài của µA cắt BC lần lượt tại D và E . Nên ta có:
 EB AB DB 16 1 EC
 EB hay B là trung điểm của EC .
 EC AC DC 32 2 2
 b) Vì B là trung điểm của EC EB BC 21 cm 
 DB 1
 Ta có: DC 2DB mà BD DC BC BD 2BD 21 DB 7 cm 
 DC 2
 DE DB BE 21 7 28 cm .
Bài 11: Cho ABC vuông tại A có AB AC . Đường cao AH , trung tuyến AM . Đường thẳng 
vuông góc với AM tại A cắt đường thẳng BC tại D . Chứng minh:
 a) AB là tia phân giác D· AH . D
 b) BH.CD BD.CH . B
 H
 M
 A C
 Lời giải
 BC 
 a) ABC vuông tại A có đường trung tuyến AM AM BM 
 2 
 MAB cân tại M M· BA M· AB (tính chất tam giác cân) 
 D· AB B· AH (cùng phụ với hai góc bằng nhau)
 Vậy AB là tia phân giác D· AH (đpcm)
 b) Vì ABC vuông tại A AB  AC nên AC là đường phân giác ngoài tại đỉnh A của ADH
 BD AD CD
 BH.CD BD.CH (đpcm)
 BH AH CH
 Trang 6