Đề cương ôn tập môn Hình học Lớp 8 - Bài 2: Định lí ta lét đảo

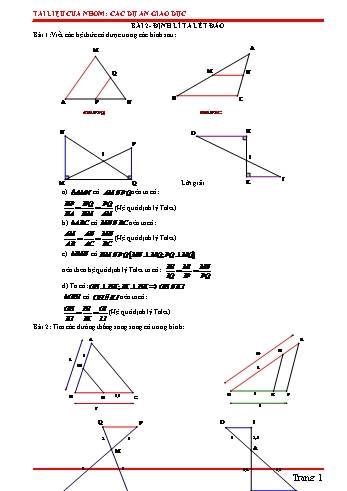
 TÀI LIỆU CỦA NHÓM: CÁC DỰ ÁN GIÁO DỤC
 BÀI 2- ĐỊNH LÍ TA LÉT ĐẢO
Bài 1:Viết các hệ thức có được trong các hình sau:
 M A
 Q M N
 B C
 A P N
 AM // PQ MN // BC
 N O H
 P
 I
 I
 J
 M Q Lời giải K
 a) AMN có AM // PQ nên ta có:
 NP NQ PQ
 (Hệ quả định lý Talet)
 NA NM AM
 b) ABC có MN // BC nên ta có:
 AM AN MN
 (Hệ quả định lý Talet)
 AB AC BC
 c) IMN có NM // PQ MN  MQ; PQ  MQ 
 NI MI MN
 nên theo hệ quả định lý Talet ta có: 
 IQ IP PQ
 d) Ta có:OH  HK; JK  HK OH // KJ
 OHI có OH // KJ nên ta có:
 OH HI OI
 (Hệ quả định lý Talet)
 KJ IK IJ
Bài 2: Tìm các đường thẳng song song có trong hình:
 A E
 H
 3 10
 6
 M
 8
 B N 3,5 C D 4 K F
 5
 7
 Q P O I
 2 3 3 2,4
 A
 M
 6 4 3,6 4,5
 Trang 1
 K N B C TÀI LIỆU CỦA NHÓM: CÁC DỰ ÁN GIÁO DỤC
 Lời giải
 +/ Ta có: 
 AM 3 1 
 AB 6 2 AM CN
  MN //AC (định lý Ta létđảo)
 CN 3,5 1 AB CB
 CB 7 2 
 +/ Ta có: 
 DH 8 4
 DE 10 5 DH DK
  HK //EF (định lý Ta létđảo)
 DK 4 DE DF
 DF 5  
 +/ Ta có: 
 MQ 2 1 
 MN 4 2 MQ MP
  PQ//KN (định lý Ta létđảo)
 MP 3 1 MN MK
 MK 6 2  
 +/ Ta có: 
 AO 3 2
 AC 4,5 3 AO AI
  IO//BC (định lý Ta létđảo)
 AI 2,4 2 AC AB
 AB 3,6 3  
Bài 3: Cho ABC có D, E lần lượt thuộc các cạnh AB, AC sao cho DE//BC . Trung tuyến AM của 
 ABC cắt DE ở N . Chứng minh N là trung điểm của DE .
 Lời giải
 A
 D E
 N
 B M C
 Ta có DE//BC DN //BM , NE//MC
 Xét ABM có DN //BM . Theo hệ quả củađịnh lý Ta lét ta có:
 AD AN DN
 1 
 AB AM BM
 Xét ACM có NE//MC . Theo hệ quả củađịnh lý Ta lét ta có:
 AE AN NE
 2 
 AC AM MC
 Trang 2 TÀI LIỆU CỦA NHÓM: CÁC DỰ ÁN GIÁO DỤC
 DN EN
 Từ 1 2 DN EN vì BM CM , hay N là trung điểm của DE .
 BM CM
Bài 4: Cho ABC có trung tuyến AM . MD là đường phân giác trong của MAB . Từ D kẻ đường 
thẳng song song với BC cắt AM và AC lần lượt tại N và E .
 a, MN là đường gì của DME .
 b, MND, MNE và MDE là các tam giác gì?
 c, Chứng minh ME là đường phân giác của AMC .
 Lời giải
 A
 D N E
 B M C
 a) Từ D kẻ đường thẳng song song với BC cắt AM và AC lần lượt tại N và E .
 DE//BC DN //BM , NE//MC
 Xét ABM có DN //BM . Theo hệ quả củađịnh lý Ta lét ta có:
 AD AN DN
 (1) 
 AB AM BM
 Xét ACM có NE//MC . Theo hệ quả củađịnh lý Ta lét ta có:
 AE AN NE
 2 
 AC AM MC
 DN EN
 Từ 1 2 DN EN vì BM CM , 
 BM CM
 hay MN là đường trung tuyến của DME .
 b) +/ Ta có DN //BM N· DM B· MD 3 (so le trong)
 Mà N· MD B· MD 4 ( MD là đường phân giác của N· MB )
 Từ 3 4 N· MD N· DM . Hay MND là tam giác cân tại N .
 +/ MND là tam giác cân ND NM , mà DN EN NE NM
 NEM cân tại N .
 +/ Cách 1:
 Ta có NE//MC N· EM E· MC (so le trong)
 Mặt khác NEM cântại N nên N· EM N· ME . Lại có N· MD B· MD
 B· MC B· MD D· MN N· ME E· MC 180O B· MC 2D· MN 2N· ME 180O
 2 D· MN N· ME 180O D· MN N· ME 90O D· ME 90O . 
 Hay MDE vuông tại M .
 Cách 2: Ta có DN EN , lại có MND là tam giác cân tại N NM ND
 Xét MDE có: DN EN MN là đường trung tuyếnứng với cạnh DE * 
 Trang 3 TÀI LIỆU CỦA NHÓM: CÁC DỰ ÁN GIÁO DỤC
 DN EN MN  1
 Mà  MN DE ** 
 DN NE DE  2
 Từ * ** MDE vuông tại M (trong một tam giác đường trung tuyếnứng với một cạnh 
 bằng một nửa cạnhấy thì tam giácđó là tam giác vuông)
 c) Ta có N· ME E· MC N· EM (theo câu b). Suy ra ME là phân giác N· MC hay ME là 
 phân giác ·AMC . Vậy ME là đường phân giác của AMC .
Bài 5: Cho ABC vuông cân ở A có đường trung tuyến BM và trọng tâm G . Lấy điểm F trên BC 
sao cho BF 2.CF . Chứng minh:
 a, GF //AC .
 b, AF  BM .
 Lời giải
 B
 D
 G F
 C
 A M
 BG BF
 a) Ta cóG là trọng tâm ABC 2 , mặt khác 2 GF //MC
 GM FC
 Mà M AC GF //AC (định lý Ta Létđảo)
 b) Giả sử AG  BC D, AD  BC (do ABC vuông cân ở A )
 GF //AC, AC  AB GF  AB
 GF  AB 
  G là trực tâm ABF BG  AF hay AF  BM .
 AD  BC
Bài 6: Cho ABC đường cao AH . Trên AH lấy D và E sao cho AD DE EH . Từ D kẻ đường 
thẳng song song với BC cắt AB tại M , cắt AC tại N . Từ E kẻ đường thẳng song song với BC cắt 
AB tại P , cắt AC tại Q .
 AD AE
 a, Tìm các tỉ số bằng với tỉ số và các tỉ số bằng với tỉ số .
 AH AH
 b, Nếu BC 15cm . Hãy tính MN, PQ .
 c, Tính diện tích tứ giác MNQP biết diện tích ABC là 540cm2 .
 Lời giải
 A
 M N
 D
 P Q
 E
 B H C
 Trang 4 TÀI LIỆU CỦA NHÓM: CÁC DỰ ÁN GIÁO DỤC
 a) Từ D kẻ đường thẳng song song với BC cắt AB tại M , cắt AC tại N . Từ E kẻ đường 
 thẳng song song với BC cắt AB tại P , cắt AC tại Q .
 Suy ra MN //PQ//BC MD//PE//BH, DN //EQ//HC
 AD AM MD AN DN 1 
 Vậy 
 AH AB BH AC HC 3 
 AE AQ EQ AP PE 2 
 AH AC HC AB BH 3 
 AM AN MN 1 1
 b) Vì MN //PQ//BC , mà BC 15cm MN .15 5
 AB AC BC 3 3
 AQ AP PQ 2 2
 MN //PQ//BC PQ .15 10
 AC AB BC 3 3
 Vậy MN 5 cm , PQ 10 cm 
 1 1 1
 c) S 540cm2 , S .AH.BC .AH.15 , 540 .AH.15 AH 72cm
 ABC ABC 2 2 2
 1
 Lại có AD DE EH DE AH DE 24
 3
 1
 Diện tích tứ giác MNQP : 5 10 .24. 180 .
 2
 Vậy diện tích tứ giác MNQP là180cm2
Bài 7: Cho tứ giác ABCD . Qua điểm E trên cạnh AD , kẻ đường thẳng song song với DC và cắt AC 
ở G . Qua G kẻ đường thẳng song song với CB và cắt AB ở H .
 GA
 a, Tìm các tỉ số bằng với tỉ số .
 GC
 b, Chứng minh HE // BD .
 Lời giải
 B
 C
 H
 G
 A E D
 GA EA
 a, Xét ACD có GE //CD , áp dụng định lý Talet ta có: (1).
 GC ED
 GA HA
 Xét ACB có GH //CB , áp dụng định Tý talet ta có: (2).
 GC HB
 GA EA HA
 Từ 1 và 2 ta có : .
 GC ED HB
 GA EA HA
 Vậy các tỉ số bằng tỉ số là ; .
 GC ED HB
 EA HA GA
 b, Theo phần a, ta có ( vì cùng bằng ). 
 ED HB GC
 Trang 5 TÀI LIỆU CỦA NHÓM: CÁC DỰ ÁN GIÁO DỤC
 EA HA
 Xét HBD có E AD, H AB mà , áp dụng định lý Talet đảo ta có HE // BD .
 ED HB
 Vậy HE // BD .
Bài 8: Cho hình thang ABCD có AB // CD và AB CD . Lấy điểm M trên cạnh AD và điểm N 
 DM BN
trên BC sao cho . Lấy điểm I trên CD sao cho MI // AC . 
 DA BC
 DI
 a, Tìm các tỉ số bằng với tỉ số .
 DC
 b, Chứng minh rằng IN // BD .
 Lời giải
 A B
 N
 M
 D I C
 DI DM
 a, Xét DAC có MI // AC , áp dụng định lý Talet ta có : (1).
 DC DA
 DM BN
 Mặt khác theo bài ra ta có (2).
 DA BC
 DI DM BN
 Từ 1 và 2 ta có : .
 DC DA BC
 DI DM BN
 Vậy các tỉ số bằng tỉ số là ; .
 DC DA BC
 DI BN DM
 b, Theo phần a, ta có (vì cùng bằng )
 DC BC DA
 DI BN
 Xét DCB có I DC , N BC mà , áp dụng định lý Talet đảo ta có IN // BD .
 DC BC
 Vậy IN // BD .
Bài 9: Cho tứ giác ABCD . Lấy điểm I trên cạnh AD sao cho AI 2.ID . Lấy điểm K trên cạnh BC 
sao cho BC 3.BK . Lấy điểm M trên cạnh CD sao cho IM // AC . Chứng minh rằng MK // BD .
 Lời giải
 B
 K
 C
 M
 A I D
 DI 1
 + Theo bài ra ta có AI 2.ID nên 1 .
 IA 2
 DI DM
 Xét DAC có MI // AC , áp dụng định lý Ta let ta có : 2 .
 IA MC
 Trang 6 TÀI LIỆU CỦA NHÓM: CÁC DỰ ÁN GIÁO DỤC
 DM 1
 Từ 1 và 2 suy ra 3 .
 MC 2
 BK 1
 Vì điểm K trên cạnh BC sao cho BC 3.BK nên 4 .
 KC 2
 BK DM
 Từ 3 và 4 suy ra .
 KC MC
 BK DM
 + Xét BCD có K BC, M DC mà (chứng minh trên), áp dụng định lý Talet đảo 
 KC MC
 ta có KM // BD . Vậy KM // BD .
Bài 10: Cho ABC . Lấy D thuộc AB và E thuộc BC . Đường thẳng qua D và song song BC cắt 
AE ở G và cắt AC ở I . Đường thẳng qua E và song song với AB cắt CD tại F .
 GD EB
 a, So sánh với .
 GI EC
 b, Chứng minh GF // AC .
 Lời giải
 A
 D G I
 F
 B E C
 a, Vì qua D kẻ một đường thẳng song song với BC nên ta có DG // BE , GI // EC .
 Xét ABE có D AB,G AE mà DG // BE , áp dụng hệ quả định lý Talet ta có :
 DG AG
 1 .
 BE AE
 Xét AEC có I AC,G AE mà GI // EC , áp dụng hệ quả định lý Talet ta có :
 GI AG
 2 .
 EC AE
 DG GI GD EB
 Từ 1 và 2 ta có : .
 BE EC GI EC
 GD EB
 Vậy .
 GI EC
 EB FD
 b, + Xét CBD có E BC, F CD mà EF // BD , áo dụng định lý Talet ta có : * 
 EC FC
 GD EB
 Theo phần a, ta có ** .
 GI EC
 FD GD
 Từ * và ** suy ra .
 FC GI
 FD GD
 + Xét DCI có G DI, F DC mà (cmt), áp dụng định lý Talet đảo ta có GF // IC .
 FC GI
 Mà A, I,C thẳng hàng nên GF // AC .
 Vậy GF // AC .
 Trang 7 TÀI LIỆU CỦA NHÓM: CÁC DỰ ÁN GIÁO DỤC
Bài 11: Cho hình thang ABCD có AB //CD và AB CD . AC cắt BD tại O , M và N lần lượt là 
trung điểm của CD và AB .
 OA
 a, Tìm tỉ số bằng với tỉ số .
 OC
 b, Chứng minh M ,O, N thẳng hàng.
 Lời giải
 A N B
 O
 D M C
 OA OB AB
 a, Xét OCD có AB //CD , áp dụng hệ quả định lý Talet ta có: .
 OC OD DC
 Vì M và N lần lượt là trung điểm của CD và AB nên AB 2.NA 2.NB, DC 2.MD 2NC .
 OA OB AB NA NB NA NB
 Do đó .
 OC OD DC MD MD MC MC
 OA OB AB NA NB NA NB
 Vậy các tỉ số bằng với tỉ số là ; ; ; ; ; .
 OC OD DC MD MD MC MC
 b, Cách 1:
 A N B
 O' O
 D M C
 Gọi O ' là giao điểm của MN và AC .
 AO ' AN
 Xét MO 'C có MC // NA , áp dụng hệ quả định lý Talet ta có 
 O 'C MC
 AO AN
 Mặt khác theo phần a, ta có .
 OC MC
 AO AO ' AO AO ' AO AO '
 Do đó: hay suy ra O trùng O ' .
 OC O 'C AO OC AO ' O 'C AC AC
 Vậy M ,O, N thẳng hàng.
 Cách 2:
 A N B
 O
 M'
 D M C
 Trang 8 TÀI LIỆU CỦA NHÓM: CÁC DỰ ÁN GIÁO DỤC
 Kéo dài NO cắt DC tại M ' .
 AO AN
 Xét M 'OC có M 'C // NA , áp dụng hệ quả định lý Talet ta có: .
 OC M 'C
 AO AN
 Theo phần a, ta có: .
 OC MC
 AN AN
 Do đó MC M 'C mà M , M ' nằm trên CD nên M trùng M ' .
 MC M 'C
 Vậy M ,O, N thẳng hàng.
 Khai thác bài toán : ‘Chứng minh rằng AD, NM , BC đồng quy ’ 
 Phương pháp giải cũng tương tự như phần b. Sau đây các em có thể tham khảo một cách làm.
 Lời giải :
 S
 A N B
 O
 M'
 D M C
 Gọi S là giao điểm của AD và BC .
 Gọi giao điểm của SN và CD là M ' . 
 Vì AB //CD mà A, N, B thẳng hàng, D, M ',C thẳng hàng nên AN // DM ' , NB // M 'C .
 SA AB
 Xét SDC có AB //CD , áp dụng hệ quả định lý Talet ta có: (3).
 SD DC
 AB AN
 Mà (Theo phần a) (4).
 DC DM
 SA AN
 Xét SDM ' có AN // DM ' , áp dụng hệ quả định lý Talet ta có: (5).
 SD DM '
 AN AN
 Từ (3), (4) và (5) suy ra : DM DM ' .
 DM DM '
 Suy ra M trùng M '. Hay AD, NM , BC đồng quy.
Bài 12: Cho hình thang ABCD có AB//CD . Gọi M là trung điểm củaCD.AM cắt BD. tại I ,cắt 
AC tại K
 IM KM
 a, Chứng minh .
 IA KB
 b, Chứng minh IK // AB // CD . A B
 c, IK cắt AD tại N
 Chứng minh rằng I là trung điểm của KN
 N K
 I
 D M C
 Trang 9 TÀI LIỆU CỦA NHÓM: CÁC DỰ ÁN GIÁO DỤC
 Lời giải:
 IM DM
 a) Vì AB// CD hay AB// DM (hệ quả của định lý Ta let)
 IA AB
 IM MC
 hay (vì DM MC )(1)
 IA AB
 KM CM
 Vì AB// CD hay AB// CM (hệ quả của định lý Ta let) (2)
 KB AB
 IM KM
 Từ (1) và (2) 
 IA KB
 IM KM
 b) Xét MAB có ( chứng minh trên)
 IA KB
 IK // AB ( định lý Ta let đảo ) mà AB// CD (gt) IK // AB// CD
 c) Xét MAC có IK // MC ( chứng minh trên)
 IA IK
 (hệ quả của định lý Ta let)(3)
 AM MC
 Xét MAD có IN // MD ( Vì IK // CD )
 IA IN
 (hệ quả của định lý Ta let)(4)
 AM MD
 IN IK
 Từ (3) và (4) mà MD MC IN IK
 MD MC
 Hay I là trung điểm của NK
Bài 13:Cho hình thang cân ABCD có AB CD , AB// CD và AB AD . Hai đường thẳng AD và 
BC cắt nhau tại E . Biết ED 15cm và CD 10cm .
 a, Chứng minh DB là tia phân giác ·ADC .
 b, Tính BE và BC .
 c, Đường thẳng song song với đáy AB cắt các đoạn thẳng AD , BC và các đường chéo BD ,
 DN CP
AC lần lượt tại M ,Q, N, P .Chứng minh .
 BD AC
 d, Chứng minh MN PQ . E
 A B
 M N P Q
 D C
Bài giải:
 a) Vì AB AD ADB cân tại A ·ADB ·ABD
 Mà AB// AD ·ABD B· DC (So le trong)
 ·ADB B· DC ( ·ABD) hay DB là phân gác của ·ADC
 Trang 10