Tài liệu ôn tập môn Toán Lớp 8 - Bài 3: Đường trung bình của tam giác, hình thang

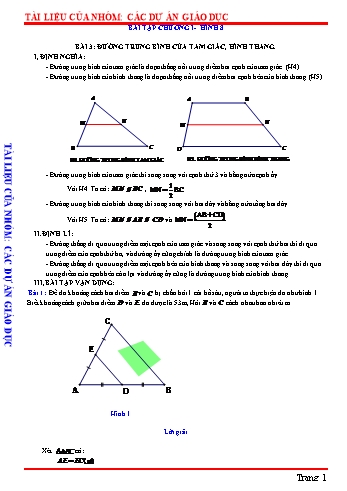
 TÀI LIỆU CỦA NHÓM: CÁC DỰ ÁN GIÁO DỤC
 BÀI TẬP CHƯƠNG I- HÌNH 8
 BÀI 3: ĐƯỜNG TRUNG BÌNH CỦA TAM GIÁC, HÌNH THANG.
 I, ĐỊNH NGHĨA:
 - Đường trung bình của tam giác là đoạn thẳng nối trung điểm hai cạnh của tam giác. (H4)
 - Đường trung bình của hình thang là đoạn thẳng nối trung điểm hai cạnh bên của hình thang. (H5)
 A A B
 N N
 M M
TÀI LIỆU CỦA NHÓM: CÁC DỰ ÁN GIÁO DỤC
 B C D C
 H4.ĐƯỜNG TRUNG BÌNH TAM GIÁC H5. ĐƯỜNG TRUNG BÌNH HÌNH THANG
 - Đường trung bình của tam giác thì song song với cạnh thứ 3 và bằng nửa cạnh ấy.
 1
 Với H4. Ta có: MN // BC , MN BC 
 2
 - Đường trung bình của hình thang thì song song với hai đáy và bằng nửa tổng hai đáy. 
 AB CD 
 Với H5. Ta có: MN // AB // CD và MN 
 2
 II. ĐỊNH LÍ:
 - Đường thẳng đi qua trung điểm một cạnh của tam giác và song song với cạnh thứ hai thì đi qua 
 trung điểm của cạnh thứ ba, và đường ấy cũng chính là đường trung bình của tam giác. 
 - Đường thẳng đi qua trung điểm một cạnh bên của hình thang và song song với hai đáy thì đi qua 
 trung điểm của cạnh bên còn lại và đường ấy cũng là đường trung bình của hình thang.
 III, BÀI TẬP VẬN DỤNG:
 Bài 1: Để đo khoảng cách hai điểm B và C bị chắn bởi 1 cái hồ sâu, người ta thực hiện đo như hình 1.
 Biết khoảng cách giữa hai điểm D và E đo được là 53m, Hỏi B và C cách nhau bao nhiêu m.
 C
 E
 A D B
 Hình 1
 Lời giải
 Xét ABC có:
 AE EC(gt)
 Trang 1 TÀI LIỆU CỦA NHÓM: CÁC DỰ ÁN GIÁO DỤC
 AD DB(gt)
 Nên DE là đường trung bình của tam giác ABC
 1
 Suy ra: DE BC ( tính chất đường trung bình trong tam giác)
 2
 Nên: BC 2.53 106(m)
 Bài 2: Để đo khoảng cách giữa hai điểm A và B bị ngăn cách bởi một hồ nước người ta đóng các cọc tại 
 các vị trí A, B , M , N , O như hình 2 và đo được MN 45m . Tính khoảng cách AB biết M , N lần lượt 
 là điểm chính giữa OA và OB.
 A B
TÀI LIỆU CỦA NHÓM: CÁC DỰ ÁN GIÁO DỤC
 45 m
 M N
 O
 Hình 2
 Lời giải
 Xét OABcó:
 AM MO(gt)
 BN NO(gt)
 Nên MN là đường trung bình của tam giác OAB
 1
 Suy ra: MN AB ( tính chất đường trung bình trong tam giác)
 2
 Nên: BC 2.45 90(m)
 Bài 3: Cho ABC cân tại A , đường cao AM , N là trung điểm của AC , kẻ Ax // BC cắt MN tại E . 
 Chứng minh:
 a, M là trung điểm của BC .
 b, ME // AB . 
 c, AE MC . 
 Lời giải
 A E
 N
 B M C Trang 2 TÀI LIỆU CỦA NHÓM: CÁC DỰ ÁN GIÁO DỤC
 a) Xét ABC cân tại A có AM là đường cao
 nên AM là đường trung tuyến của ABC
 Suy ra: M là trung điểm của BC
 b) Xét ABC có:
 M là trung điểm BC
 N là trung điểm AC
 Nên MN là đường trung bình của ABC
 Suy ra MN // BC ( tính chất đường trung bình trong tam giác)
 Vậy ME // AB
TÀI LIỆU CỦA NHÓM: CÁC DỰ ÁN GIÁO DỤC 
 c) Xét EAM và MCN có:
 E· AN M· CN ( hai góc so le trong vì AE // MC )
 AN NC (gt)
 A· NE M· NC (hai góc đối đỉnh)
 Vậy EAM MCN (g – c – g)
 Suy ra : AE MC ( hai cạnh tương ứng)
 Bài 4: Cho ABC có AB 5cm,AC 7cm,BC 9cm . Kéo dài AB lấy điểm D sao cho BD BA , Kéo 
 dài AC lấy điểm E sao cho CE CA . Kéo dài đường trung tuyến AM của ABC lấy MI MA.
 a, Tính độ dài các cạnh của ADE .
 b, Chứng minh DI // BC .
 c, Chứng minh ba điểm D , I , E thẳng hàng.
 Lời giải
 A
 B C
 M
 D I E
 a) AD AB BD 2AB 2.5 10(cm) (vì BD AB)
 AE AC CE 2AC 2.7 14(cm) (vì AC CE )
 Xét ADE có:
 B là trung điểm AD (gt)
 C là trung điểm AE (gt) 
 Nên BC là đường trung bình của ADE
 Trang 3 TÀI LIỆU CỦA NHÓM: CÁC DỰ ÁN GIÁO DỤC
 1
 Suy ra BC DE ( tính chất đường trung bình trong tam giác) 
 2
 Nên: DE 2BC 2.9 18(cm)
 b) Xét ADI có:
 B là trung điểm AD (gt)
 M là trung điểm AI (gt) 
 Nên BM là đường trung bình của ADI
 Suy ra : BM // DI ( tính chất đường trung bình trong tam giác)
 Vậy BC // DI (1)
 c) Xét AEI có:
 C là trung điểm AE (gt)
TÀI LIỆU CỦA NHÓM: CÁC DỰ ÁN GIÁO DỤC M là trung điểm AI (gt) 
 Nên CM là đường trung bình của AEI
 Suy ra : CM // EI ( tính chất đường trung bình trong tam giác)
 Vậy BC // EI (2) 
 Từ (1) và (2) suy ra D,I,E thẳng hàng ( theo tiên đề Ơ-clit)
 Bài 5: Cho ABC cân tại A , có M là trung điểm của BC , kẻ Mx//AC cắt AB tại E , Kẻ My//AB cắt AC tại 
 F . Chứng minh:
 a, E,F lần lượt là trung điểm của AB và AC . A
 1
 b, EF BC
 2
 c, ME MF; AE AF E F
 B M C
 Lời giải
 a, Vì M là trung điểm của BC và Mx//AC cắt AB tại E nên Mx đi qua trung điểm của AB E là trung 
 điểm của AB ( Định lý)
 Chứng minh tương tự F là trung điểm của AC .
 b, Vì E;F là trung điểm của AB; AC nên EF là đường trung bình của VABC .
 1
 EF BC ( Tính chất đường trung bình trong tam giác).
 2
 c, 
 +) Trong VABC
 Có M ; E là trung điểm của BC và AB nên ME là đường trung bình của VABC
 1
 ME AC ( Tính chất đường trung bình trong tam giác).
 2
 Có M ; F là trung điểm của BC và AC nên MF là đường trung bình của VABC
 1
 MF AB ( Tính chất đường trung bình trong tam giác).
 2
 Mà VABC cân tại A nên AB AC
 Trang 4 TÀI LIỆU CỦA NHÓM: CÁC DỰ ÁN GIÁO DỤC
 1
 ME MF ( AB )
 2
 1 1
 +) Vì E;F là trung điểm của AB; AC ( chứng minh câu a) nên AE AB và AF AC
 2 2
 Mà VABC cân tại A nên AB AC
 AE AF
 Bài 6: Cho VABC vuông tại A có AM là đường trung tuyến. N là trung điểm của AC
 a, Chứng minh MN  AC . A
 b, VAMC là tam giác gì? Vì sao?
 c, Chứng minh 2AM BC .
 N
TÀI LIỆU CỦA NHÓM: CÁC DỰ ÁN GIÁO DỤC
 Lời giải
 a, TrongVABC có AM là đường trung tuyến
 B M C
 M là trung điểm của BC
 Có N là trung điểm của AC (gt)
 Suy ra MN là đường trung bình của VABC
 MN //AB (Tính chất đường trung bình của tam giác)
 mà AB  AC (gt )
 MN  AC ( quan hệ từ vuông góc đến song song).
 b, VAMC là tam giác cân tại M vì có MN là đường trung tuyến đồng thời là đường cao.
 c, Vì VAMC là tam giác cân tại M nên AM MC
 Do M là trung điểm của BC nên 2MC BC
 Từ đó suy ra 2AM BC .
 Bài 7: Cho VABC trên cạnh AB lấy D và E sao cho AD DE EB . Từ D , E kẻ các đường thẳng song 
 song với BC cắt AC lần lượt tại M và N . Chứng minh:
 a, M là trung điểm của AN
 b, AM MN NC
 c, 2EN DM BC
 Lời giải
 A
 D M
 E N
 B C
 a, Trong VAEN có D là trung điểm của AE và DM //EN nên DM đi qua trung điểm của cạnh 
 AN
 M là trung điểm của AN .
 b, Xét tứ giác DMCB có DM //BC nên tứ giác DMCB là hình thang.
 Có E là trumg điểm BD và EN //BC nên EN đi qua trung điểm của cạnh bên còn lại.
 Trang 5 TÀI LIỆU CỦA NHÓM: CÁC DỰ ÁN GIÁO DỤC
 N là trung điểm của MC MN NC (1)
 Có M là trung điểm của AN AM MN (2)
 Từ (1) và (2) suy ra AM MN NC
 c, Trong hình thang DMCB ( DM //BC ) có E; N lần lượt là trung điểm của DB;MC
 EN là đường trung bình của hình thang DMCB
 2EN DM BC ( Tính chất đường trung bình của hình thang).
 Bài 8: Cho VABC trung tuyến AM . Trên AC lấy E ; F sao cho AE EF FC ; BE cắt AM tại O
 a, Tứ giác OEFM là hình gì? Vì sao?
 b, Chứng minh BO 3OE
 Lời giải
 A
TÀI LIỆU CỦA NHÓM: CÁC DỰ ÁN GIÁO DỤC E
 O
 F
 B M C
 a, Trong VCBE có M ;F lần lượt là trung điểm của BC;EC nên MF là đường trung bình của VCBE
 MF //BE MF //OE
 Tứ giác OEFM có MF //OE nên tứ giác là hình thang.
 b, Trong VBEC có MF là đường trung bình BE 2MF (1)
 Trong VAMF có E là trung điểm của AF và OE //MF nên OE đi qua trung điểm của cạnh AM O là 
 trung điểm của AM
 Trong VAMF có E là trung điểm của AF và O là trung điểm của AM nên OE là đường trung bình của 
 VAMF MF 2OE (2)
 Từ (1) và (2) suy ra BO BE OE 2MF OE 2.2OE OE 3OE
 Bài 9: Cho VABC , trung tuyến AM . Gọi D là trung điểm của AM , BD cắt AC tại E . Kẻ MK //BE ( K
 thuộc EC ). Chứng minh:
 a, K là trung điểm của CE .
 b, CE 2AE
 Lời giải
 A
 E
 D
 K
 B M C
 a, Có AM là trung tuyến của VABC nên M là trung điểm của BC
 Trong VBEC có M là trung điểm của BC và MK //BE suy ra MK đi qua trung điểm của EC
 Trang 6 TÀI LIỆU CỦA NHÓM: CÁC DỰ ÁN GIÁO DỤC
 K là trung điểm của EC
 b, Trong VAMK có D là trung điểm của AM và DE //MK ( do MK //BE )
  DE đi qua trung điểm của AK E là trung điểm của AK AE EK (1)
 Mà K là trung điểm của EC 2EK EC (2)
 Từ (1) và (2) 2AE EC
 Bài 10: Cho VABC cân tại A có M là trung điểm của đường cao AH . CM cắt AB tại D , kẻ Hx//CD cắt 
 AB tại E . Chứng minh:
 a, AD DE
 b, AB 3AD
 c, CD 4MD
 Lời giải A
TÀI LIỆU CỦA NHÓM: CÁC DỰ ÁN GIÁO DỤC a,Trong VAHE có M là trung điểm AH và DM //EH ( do Hx//CD ) 
 nên DM đi qua trung điểm của cạnh AE
 D là trung điểm của AE D
 DA DE M
 b, Do VABC cân tại A có AH là đường cao đồng thời là trung tuyến E
 H là trung điểm của BC
 Trong VBDC có H là trung điểm của BC và Hx//DC cắt BD tại E
 nên Hx đi qua trung điểm của cạnh BD
 E là trung điểm của BD BE ED B H C
 Mà DA DE ( Câu a)
 BE ED DA và AB DA DE EB
 AB 3AD
 c, 
 Trong VAHE có D;M lần lượt là trung điểm của AE; AH nên DM là đường trung bình của VAHE
 1
 DM EH
 2
 Trong VBDC có H ;E lần lượt là trung điểm của BC;BD nên HE là đường trung bình của VBDC
 1
 HE CD
 2
 CD 2HE và HE 2DM
 CD 2HE 2.2DM 4MD
 Trang 7 TÀI LIỆU CỦA NHÓM: CÁC DỰ ÁN GIÁO DỤC
TÀI LIỆU CỦA NHÓM: CÁC DỰ ÁN GIÁO DỤC
 Trang 8