Đề ôn tập kiểm tra đợt 9 môn Toán Lớp 12 - Tổ 8 - Chủ đề: Tính đơn điệu của hàm số - Năm học 2020-2021 (Có đáp án)

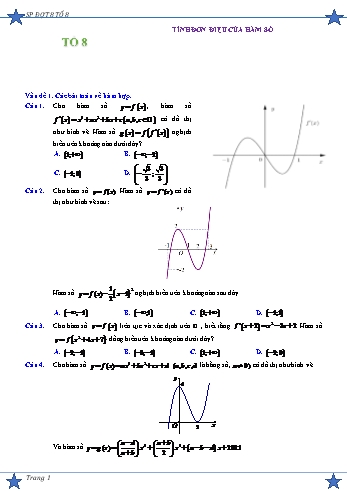
 SP ĐỢT 8 TỔ 8 
 TÍNH ĐƠN ĐIỆU CỦA HÀM SỐ
 TỔ 8
Vấn đề 1. Các bài toán về hàm hợp.
Câu 1. Cho hàm số y f x , hàm số 
 f x x3 ax2 bx c a,b,c ¡ có đồ thị 
 như hình vẽ. Hàm số g x f f x nghịch 
 biến trên khoảng nào dưới đây?
 A. 1; .B. ; 2 .
 3 3 
 C. 1;0 . D. ; .
 3 3 
Câu 2. Cho hàm số y f (x) . Hàm số y f (x) có đồ 
 thị như hình vẽ sau:
 1 2
 Hàm số y f (x) x 1 nghịch biến trên khoảng nào sau đây.
 2
 A. ; 1 .B. ;1 . C. 1; . D. 1;1 .
Câu 3. Cho hàm số y f x liên tục và xác định trên ¡ , biết rằng f x 2 x2 3x 2. Hàm số 
 y f x2 4x 7 đồng biến trên khoảng nào dưới đây?
 A. 2; 1 . B. 3; 1 . C. 1; . D. 2;0 .
Câu 4. Cho hàm số y f (x) ax3 bx2 cx d (a,b, c, d là hằng số, a 0) có đồ thị như hình vẽ.
 y
 4
 O 2 x
 a d 4 a b 3
 Và hàm số y g(x) x x a b d x 2021.
 a b 2 
 Trang 1 SP ĐỢT 8 TỔ 8 
 Hàm số y f ( x2 1) g( x2 1) đồng biến trên khoảng nào?
 A. 1;0 . B. 1;2 . C. 2;2 . D. 0;2 .
Câu 5. Cho hàm số bậc bốn y f (x) có đồ thị f (x) là đường đậm như hình vẽ và hàm số bậc ba 
 y g(x) có đồ thị là đường lợt như hình vẽ. Hàm số h(x) f g(x) đồng biến trên
 A. ( 6; 3) .B. (1;3) . C. (3;6) D. ( 1;1) .
 1
Câu 6. Cho hàm số y f x có đạo hàm trên ¡ và thoả f 3 f 3 . Biết rằng hàm số 
 2
 y f x là một hàm số bậc ba có đồ thị như hình vẽ sau:
 2
 Hỏi hàm số g x f 3 x f 3 x nghịch biến trên khoảng nào sau đây:
 A. 3;1 . B. ; 3 . C. 0;2 .D. 2;6 .
Câu 7. Cho đồ thị hàm số y f 3 x có đồ thị như hình vẽ bên dưới.
 Hàm số y f x nghịch biến trên khoảng nào dưới đây?
 A. ; 1 .B. 1;1 .C. 1; . D. 1;3 .
 Trang 2 SP ĐỢT 8 TỔ 8 
Câu 8. Cho hàm số y f x có đạo hàm liên tục trên ¡ và đồ thị hàm số y f ' x như hình bên.
 Hỏi hàm số g x f 1 2x nghịch biến trên khoảng nào trong các khoảng sau?
 A. 2; . B. ; 2 . C. 1;3 . D. 0;2 
Vấn đề 2. Các bài toán về hàm phân thức có tham số
 2020cos x 1
Câu 9. Tìm tất cả các giá trị thực của tham số m để hàm số y nghịch biến trên khoảng 
 2021cos x m
 0; .
 3 
 6063 6063
 A. m .B. m .
 2020 2020
 6063 2021 
 C. m . D. m ;2021 .
 2020 2 
 1 m
Câu 10. Có bao nhiêu giá trị nguyên âm của m để hàm số y x 5 đồng biến trên 5; ?
 x 2
 A. 10.B. 8 .C. 9 .D. 11.
 sin2 x m 
Câu 11. Số giá trị nguyên m thuộc  20; 20 để hàm số y 2 đồng biến trên khoảng ; ?
 sin x 1 2 
 A. 40 . B. 39 . C. 22 .D. 21.
 mx 2
Câu 12. Cho hàm số y ( m là tham số). Tính T là tổng các giá trị nguyên của tham số m để 
 m x
 hàm số nghịch biến trên khoảng ;0 ?
 A. T 0 . B. T 2 .C. T 1. D. T 1.
 mx 8
Câu 13. Cho hàm số y ( m là tham số thực). Có bao nhiêu giá trị nguyên của tham số m thuộc 
 x 2m
 đoạn  2020;2020 để hàm số đồng biến trên khoảng 2; ?
 A. 2018 . B. 2017 . C. 4036 .D. 4034 .
 x2 4x
Câu 14. Tìm tất cả giá trị thực của tham số m để hàm số y đồng biến trên 1; 
 x m
 1 1 1 
 A. m ;2 \ 1 . B. m 1;2 \ 1. C. m 1; . D. m 1; .
 2 2 2 
 ln x 6
Câu 15. Có bao nhiêu giá trị nguyên dương của tham số m để hàm số y đồng biến trên 
 ln x 2m
 khoảng 1, e ?
 A. 2 . B. 1. C. 4 . D. 3 .
 Trang 3 SP ĐỢT 8 TỔ 8 
 2 tan x 1
Câu 16. Tìm tất cả các giá trị thực của tham số m sao cho hàm số y đồng biến trên khoảng 
 tan x m
 0; ?
 4 
 1 1
 A. m 0. B. m . C. 0 m . D. m 0;m 1.
 2 2
 mln x 2
Câu 17. Tìm số các giá trị nguyên âm của m để hàm số y đồng biến trên e2 ; là
 ln x m 3
 A. 2 . B. vô số. C. 0. D. 1.
 mf x 2020
Câu 18. Cho hàm số f x x2 3x 3. Số giá trị nguyên m để hàm số y nghịch biến 
 f x m
 trên khoảng 0; là
 A. 42 . B. 88 . C. 41.D. 89 .
 x m
Câu 19. Có tất cả bao nhiêu giá trị nguyên của m để hàm số y đồng biến trên từng khoảng xác 
 mx 4
 định?
 A. 4 . B. 3 . C. 5 . D. 2 .
Câu 20. Cho hàm số y = f (x) liên tục trên ¡ và có bảng xét dấu đạo hàm như sau:
 Có bao nhiêu giá trị nguyên của tham số m để hàm số y = f (cosx + m) đồng biến trên khoảng 
 æ- p ö
 ç ;0÷.
 èç 2 ø÷
 A. 0 . B. 1. C. 2 . D. 3 .
Vấn đề 3. Các bài toán về hàm đa thức có tham số
Câu 21. Tìm tất cả các giá trị của tham số m để hàm số y e3x 6e2x mex 3 nghịch biến trên khoảng 
 0;ln3 .
 A. m 12 . B. m 12 . C. m 15 . D. m 15 .
 1 1
Câu 22. Cho hàm số y f x x3 3x2 9x . Đặt g x , với m là tham số. 
 4 f 2 x 6 2x m 
 Tìm số giá trị nguyên của tham số m để hàm số g x nghịch biến trên 2;3 .
 A. 6. B. 4 . C. 1 . D. 3.
Câu 23. Cho hàm số f x x3 3x 2 . Có tất cả bao nhiêu giá trị nguyên của tham số m để hàm số 
 g x f f x m nghịch biến trên khoảng 1;1 .
 A. 1. B. 2. C. 0. D. 4.
 2 3
Câu 24. Cho các hàm số f x x3 4x m và g x x2 2020 x2 2021 x2 2022 . Có bao 
 nhiêu giá trị nguyên của tham số m  2020;2020 để hàm số g f x đồng biến trên 2;5 ?
 A. 2020 . B. 2021. C. 2022 . D. 2023.
 Trang 4 SP ĐỢT 8 TỔ 8 
Câu 25. Gọi S là tập hợp tất cả các giá trị thực của tham số m để hàm số 
 f x m2 x5 mx3 m2 m 20 x2 2019 nghịch biến trên ¡ . Tổng giá trị của tất cả các 
 phần tử thuộc S bằng
 A. 4. B. 1. C. 1. D. 5 .
 5 15 4 5 2 2 3 
Câu 26. Cho hàm số y x m m 2 x 3m 6m 1 x 5m . Hàm số đồng biến trên ; 
 4 2 2 
 khi m a;b . Tính a b ?
 A. 1. B. 2 . C. 4 . D. 0 .
Câu 27. Có bao nhiêu giá trị nguyên của tham số m thuộc 30;30 để hàm số 
 3 2 
 y sin x 3cos x msin x 1 đồng biến trên đoạn 0; .
 2 
 A. 28 . B. 31. C. 30 . D. 29 .
 2
Câu 28. Giả sử x0 là nghiệm của phương trình ax bx c 0 a 0 . Cho hàm số y f x Hx với 
 b c 
 H max ; . Tìm tất các các giá trị của tham số a sao cho hàm số g x f x ax 
 a a 
 nghịch biến trên ¡ .
 2 2 x 1
 x0 x0 1 x0 0
 A. a . B. a . C. a . D. a 2 .
 x0 1 x0 x0 1 x0
Câu 29. Cho hàm số f (x) x3 3m.x2 3x2 12m.x 4 12m . S là tập các giá trị m thỏa mãn: có đúng 
 2 giá trị c ¢ để phương trình f (x) c có 3 nghiệm phân biệt. Mệnh đề nào dưới đây là đúng?
 A. (0, 05;0,15)  S. . B. (0,1;0,2)  S. . C. (0,15;0, 25)  S.. D. (0, 2;0,3)  S.
 5
 x m 3
Câu 30. Cho hàm số y 1 x (2 m)x ( m là tham số). Gọi S là tập hợp các giá trị nguyên 
 5 3 
 dương của tham số m để hàm số đã cho đồng biến trên khoảng (4; ). Tính số phần tử của S.
 A. 2. B. 18. C. 3. D. 19.
Câu 31. Gọi S tập hợp là tất cả các giá trị của tham số thực m để hàm số
 1 3 2 2 
 y sin x m 1 sin x m 2m sin x 3 nghịch biến trên khoảng ; . Tìm số phần 
 3 2 2 
 tử của S.
 A. 3. B. 0. C. 1. D. 2.
Vấn đề 4. Ứng dụng tính đơn điệu.
Câu 32. Có bao nhiêu giá trị nguyên của tham số m để phương trình m 2 m 2cos x cos x có 
 nghiệm thực?
 A. 0. B. 2. C. 1. D. 3
 x 1
Câu 33. Cho hàm số f x . Có bao nhiêu số nguyên m [ 10;10] để bất phương trình 
 x 2
 f sin x cos x 2 log m có nghiệm thực.
 A. 2 . B. 13. C. 12. D. 3 .
Câu 34. Tìm tham số m để hàm số y log m x2 4 x 1 có tập xác định là .
 2020 ¡
 5 5
 A. m 5 . B. m . C. m 1. D. m .
 2 2
 Trang 5 SP ĐỢT 8 TỔ 8 
Câu 35. Có bao nhiêu giá trị nguyên của tham số m để phương trình 
 3
 5x 2 m 3x x3 6x2 9x m 17 .5x 2 5x 1 có ba nghiệm phân biệt.
 A. 0. B. 1. C. 2. D. 3.
Câu 36. Cho hàm số f (x) 2x4 4x 2m . Tính tổng tất cả các giá trị nguyên của tham số m để phương 
 trình f 4 f (x) m x4 m có nghiệm thuộc 0;1 .
 A. 20 . B. 10 . C. 14. D. 15 .
Câu 37. Có bao nhiêu giá trị nguyên của x thỏa mãn bất phương trình 
 7x 7 7x 6 2 49x2 7x 42 181 14x ?
 A. 4 . B. 5 . C. 6 . D. 7 .
Câu 38. Biết rằng các số thực a,b thay đổi sao cho hàm số f x x3 x a 3 x b 3 luôn đồng 
 biến trên khoảng ; . Tìm giá trị nhỏ nhất của biểu thức P a2 b2 4a 4b 2 .
 A. 4 . B. 2 . C. 0 . D. 2 .
Câu 39. Cho hàm số y f (x) xác định trên ¡ và có đạo hàm f (x) thỏa mãn 
 f (x) 1 x x 2 .g x 2020 trong đó g x 0,x ¡ . Hàm số 
 y f (1 x) 2020x 2021 nghịch biến trên khoảng nào?
 A. 1; . B. 0;3 . C. ;3 . D. 3; .
Câu 40. Cho hàm số y f x liên tục trên ¡ có đồ thị như hình vẽ. Có bao nhiêu giá trị nguyên của m 
 để phương trình f 3sinx 4cosx f m m 1 có nghiệm x ¡ ?
 y
 1
 -1 O 1 2 x
 A. 3 . B. 2 . C. 4 . D. 5 .
 2
Câu 41. Cho phương trình 9 x m .log x2 2x 3 3 x 2x.log 2 x m 2 0. Có bao nhiêu giá trị 
 3 3 1 
 3
 nguyên của m để phương trình có 3 nghiệm?.
 A. 4 . B. 1. C. 3 . D. 2 .
 Trang 6 SP ĐỢT 8 TỔ 8 
 Bảng đáp án
 1.B 2.A 3.C 4.D 5.C 6.D 7.B 8.B 9.B 10.B
 11.D 12.D 13.A 14.D 15.A 16.A 17.C 18.A 19.B 20.C
 21.D 22.D 23.C 24.B 25.D 26.B 27.B 28.C 29.B 30.B
 31.C 32.B 33.A 34.D 35.D 36.D 37.B 38.B 39.D 40.C
 41.B
Câu 1. Cho hàm số y f x , hàm số f x x3 ax2 bx c a,b,c ¡ có đồ thị như hình vẽ
 Hàm số g x f f x nghịch biến trên khoảng nào dưới đây?
 3 3 
 A. 1; .B. ; 2 . C. 1;0 . D. ; .
 3 3 
 Lời giải
 Chọn B
 Vì các điểm 1;0 , 0;0 , 1;0 thuộc đồ thị hàm số y f x nên ta có hệ:
 1 a b c 0 a 0
 3 2
 c 0 b 1 f x x x f '' x 3x 1
 1 a b c 0 c 0
 Ta có: g x f f x g x f f x . f '' x 
 Xét g x 0 g x f f ' x . f x 0 3x2 1 . f x3 x 0
 x 1
 x3 x 0 
 3 x 0
 x x 1 
 x x1(x1 1,325 )
 x3 x 1 
 x x (x 1,325)
 2 2 2
 3x 1 0 
 3
 x 
 3
 Bảng biến thiên
 Dựa vào bảng biến thiên ta có g x nghịch biến trên ; 2 .
Câu 2. Cho hàm số y f (x) . Hàm số y f (x) có đồ thị như hình vẽ sau:
 Trang 7 SP ĐỢT 8 TỔ 8 
 1 2
 Hàm số y f (x) x 1 nghịch biến trên khoảng nào sau đây.
 2
 A. ; 1 .B. ;1 . C. 1; . D. 1;1 .
 Lời giải
 Chọn A
 1 2
 Đặt g x f (x) x 1 g x f x x 1 .
 2
 g x f x x 1 0 f x x 1.
 Đường thẳng d: y x 1 cắt đồ thị y f (x) tại các điểm có hoành độ lần lượt tại x 1, x 1, 
 và x 3.
 Suy ra g x 0 có ba nghiệm phân biệt x 1, x 1 và x 3.
 Bảng biến thiên của g x 
 1 2
 Từ bảng biến thiên ta có hàm số y f (x) x 1 nghịch biến trên khoảng ; 1  1;3 .
 2
Câu 3. Cho hàm số y f x liên tục và xác định trên ¡ , biết rằng f x 2 x2 3x 2. Hàm số 
 y f x2 4x 7 đồng biến trên khoảng nào dưới đây?
 A. 2; 1 . B. 3; 1 . C. 1; . D. 2;0 .
 Trang 8 SP ĐỢT 8 TỔ 8 
 Lời giải
 Chọn C
 Ta có:
 f x 2 x2 3x 2 x 1 x 2 f x x 2 1 x 2 2 x 3 x 4 .
 x 3
 Khi đó: f x 0 .
 x 4
 Đặt y g x f x2 4x 7 .
 2x 4 0
 Ta có: g x 2x 4 . f x2 4x 7 0 
 2
 f x 4x 7 0
 x 2
 x 2
 2 x 2
 2 x 2 0
 x 4x 7 3 x 1 .
 2 x 1
 x 4x 7 4 x 3
 x 3
 Bảng xét dấu g x :
 Dựa vào bảng biến thiên, ta có: hàm số y g x f x2 4x 7 đồng biến trên khoảng 1; .
Câu 4. Cho hàm số y f (x) ax3 bx2 cx d (a,b, c, d là hằng số, a 0) có đồ thị như hình vẽ.
 y
 4
 O 2 x
 a d 4 a b 3
 Và hàm số y g(x) x x a b d x 2021.
 a b 2 
 Hàm số y f ( x2 1) g( x2 1) đồng biến trên khoảng nào?
 A. 1;0 . B. 1;2 . C. 2;2 . D. 0;2 .
 Lời giải
 FB tác giả: Giang Phó
 Chọn D
 Ta có: y ax3 bx2 cx d y ' 3ax2 2bx c .
 y '(0) 0 c 0 a 1
 y(0) 4 d 4 b 3
 Theo đề ra ta có: .
 y '(2) 0 12a 4b c 0 c 0
 y(2) 0 8a 4b 2c d 0 d 4
 Trang 9 SP ĐỢT 8 TỔ 8 
 Suy ra hàm số: y f (x) x3 3x2 4.
 3
 y g(x) x4 x3 2021.
 2
 3
 Và hàm số: y f (x) g(x) x4 3x2 2025 .
 2
 Vậy: y f ( x2 1) g( x2 1) .
 3
 (x2 1)2 3 x2 1 2025 .
 2
 3 4047
 x4 .
 2 2
 y ' 6x3 .
 Hàm số đồng biến y ' 0 x3 0 x 0 .
 Vậy hàm số y f ( x2 1) g( x2 1) đồng biến trên khoảng 0, .
Câu 5. Cho hàm số bậc bốn y f (x) có đồ thị f (x) là đường đậm như hình vẽ và hàm số bậc ba 
 y g(x) có đồ thị là đường lợt như hình vẽ. Hàm số h(x) f g(x) đồng biến trên
 A. ( 6; 3) .B. (1;3) . C. (3;6) D. ( 1;1) .
 Lời giải
 FB tác giả: DuongPham
 Ta có h (x) g (x) f g(x) .
 x 1
 x 1 
 x 0
 g '(x) 0 g(x) 0 
 h'(x) 0 x 2 .
 f ' g(x) 0 g(x) 4 
 x 2
 g(x) 4 
 x 3
 Bảng xét dấu
 Dựa vào bảng xét dấu ta có h(x) đồng biến trên (2; ) nên đồng biến trên (3;6) .
 Trang 10