Đề thi thử tốt nghiệp THPT Lần I môn Toán Lớp 12 - Mã đề: 132 - Năm học 2020-2021 - Trường THPT Chuyên Nguyễn Trãi (Có đáp án)

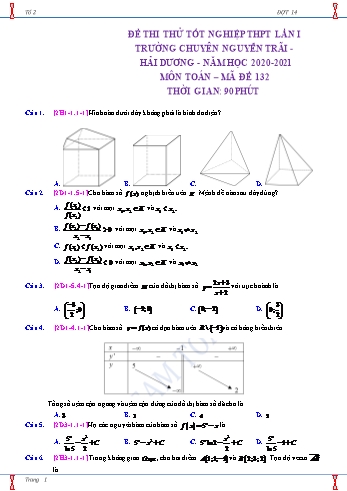
 Tổ 2 ĐỢT 14
 ĐỀ THI THỬ TỐT NGHIỆP THPT LẦN I
 TRƯỜNG CHUYÊN NGUYỄN TRÃI - 
 HẢI DƯƠNG - NĂM HỌC 2020-2021
 MÔN TOÁN – MÃ ĐỀ 132
 THỜI GIAN: 90 PHÚT
Câu 1. [2H1-1.1-1] Hình nào dưới đây không phải là hình đa diện? 
 A. B. C. D. 
Câu 2. [2D1-1.5-1] Cho hàm số f (x) nghịch biến trên K . Mệnh đề nào sau đây đúng? 
 f (x1)
 A. 1 với mọi x1, x2 K và x1 x2.
 f (x2 )
 f (x2 ) f (x1)
 B. 0 với mọi x1, x2 K và x1 x2 .
 x2 x1
 C. f (x1) f (x2 ) với mọi x1, x2 K và x1 x2.
 f (x2 ) f (x1)
 D. 0 với mọi x1, x2 K và x1 x2 .
 x2 x1
 2x 3
Câu 3. [2D1-5.4-1] Tọa độ giao điểm M của đồ thị hàm số y với trục hoành là
 x 2
 3 3 
 A. ;0 . B. 2;0 . C. 0; 2 .D. 0; .
 2 2 
Câu 4. [2D1-4.1-1] Cho hàm số y f (x) có đạo hàm trên R \ 1 và có bảng biến thiên
 Tổng số tiệm cận ngang và tiệm cận đứng của đồ thị hàm số đã cho là
 A.3 B. 1 C. 4 D. 2
Câu 5. [2D3-1.1-1] Họ các nguyên hàm của hàm số f x 5x x là 
 5x x2 x2 5x
 A. C . B. 5x x2 C . C. 5x ln 2 C . D. 1 C .
 ln5 2 2 ln5
  
Câu 6. [2H3-1.1-1] Trong không gian Oxyz , cho hai điểm A 1;1; 1 và B 2;3;2 . Tọa độ vectơ AB
 là 
Trang 1 Tổ 2 ĐỢT 14
 A. 1; 2; 3 . B. 1;2;3 . C. 3;4;1 . D. 1;2;1 .
Câu 7. [2H1-3.2-1] Cho khối chóp S.ABCD có đáy ABCD là hình vuông cạnh 1. Biết SA vuông góc 
 với ABCD và SA 3 . Thể tích của khối chóp S.ABCD là:
 1 3 3
 A. . B. 3 . C. . D. .
 4 6 3
Câu 8. [2D1-5.6-1] Cho hàm số y x3 2x 1có đồ thị C . Hệ số góc của tiếp tuyến với C tại 
 điểm M 1;2 bằng:
 A. 3 . B. 5 . C. 25 . D. 1.
 3
Câu 9. [2D2-1.2-1] Cho biểu thức P x 4 . x5 , x 0 . Khẳng định nào sau đây là đúng.
 1 1
 A. P x2 . B. P x 2 . C. P x 2 . D. P x 2 .
Câu 10. [2D1-2.2-1] Cho hàm số y f x liên tục trên ¡ \ x2 và có bảng biến thiên sau
 Mệnh đề nào sau đây đúng?
 A. Hàm số có hai điểm cực đại, một điểm cực tiểu.
 B. Hàm số có một điểm cực đại, một điểm cực tiểu.
 C. Hàm số có một điểm cực đại, hai điểm cực tiểu.
 D. Hàm số có một điểm cực đại, không có điểm cực tiểu.
Câu 11. [2D2-5.1-1] Tìm tất cả các giá trị thực của m để phương trình 2020x m có nghiệm thực. 
 A. m 0 . B. m 0 . C. m 1. D. m 0 . 
Câu 12. [1D3-4.3-1] Cho cấp số nhân un có u1 5,q 2 . Số hạng thứ 6 của cấp số nhân đó là 
 1
 A. . B. 25 . C. 32 . D. 160.
 160
Câu 13. [2D1-5.3-2] Cho hàm số y f x xác định, liên tục trên R và có bảng biến thiên như sau:
 Số nghiệm của phương trình f x 1 0 .
 A. 1. B. 3. C. 0. D. 2.
Câu 14. [2D3-1.1-1] Họ nguyên hàm của hàm số f x sin x 4x là
 A. cos x 4x2 C . B. cos x 4x2 C .
 C. cos x 2x2 C . D. cos x 2x2 C .
Trang 2 Tổ 2 ĐỢT 14
Câu 15. [2H1-3.2-2] Cho lăng trụ đứng ABC.A B C có đáy ABC vuông cân tại A và AB AC 2 ;
 cạnh bên AA 3 . Tính thể tích khối lăng trụ ABC.A B C .
 A. 6 . B. 12 . C. 3 . D. 4 .
Câu 16. [2D1-1.1-2] Cho hàm số y f x liên tục trên ¡ và có đạo hàm f x x 1 3 x . Hàm 
 số y f x đồng biến trên khoảng nào dưới đây?
 A. 1;0 . B. ;0 . C. 3; . D. ; 1 .
Câu 17. [2D1-3.1-2] Biết rằng hàm số f x x3 3x2 9x 28 đạt giá trị nhỏ nhất trên đoạn 0;4 tại 
 x0 . Giá trị của x0 bằng: 
 A. 4 . B. 0 . C. 3 .D. 1 .
Câu 18. [2D1-5.1-1] Đường cong ở hình bên là đồ thị của một trong bốn hàm số dưới đây. Hàm số đó là 
 hàm số nào?
 A. y x3 3x2 2 . B. y x3 3x2 2 C. y x3 3x2 2. D. y x3 3x2 2.
 x 1
Câu 19. [2D1-4.1-1] Đồ thị hàm số y có bao nhiêu đường tiệm cận đứng và đường tiệm cận 
 x
 ngang?
 A. 2 . B. 3 C. 1 D. 0 .
Câu 20. [2D2-3.2-1] Với a là số thực dương tùy ý, log2 (2a) bằng:
 A. 1 log2 a B. 2log2 a C. 2 log2 a D. 1 log2 a
Câu 21. [2H2-2.1-1] Thể tích của khối cầu có đường kính bằng 2 là : 
 4 32 
 A. 4 .B. . C. .D. .
 3 3 3
Câu 22. [2H3-1.1-1] Trong không gian Oxyz ,điểm nào dưới đây là hình chiếu vuông góc của điểm 
 A 3;2;4 trên mặt phẳng Oxy .
 A. P 3;2;0 . B. Q 3;0;4 . C. M 0;2;4 . D. N 0;0;4 .
Câu 23. [2H3-1.2-2] Trong không gian Oxyz góc giữa hai vectơ j 0;1;0 và u 1; 3;0 là
 A. 120 .B. 30 .C. 60 .D. 150 .
 2
Câu 24. [2D2-4.1-2] Tìm tập xác định của hàm số y log2020 3x x .
 A. D ;03; .B. D ;0  3; .
 C. D 0;3 .D. D 0;3.
 2 2
Câu 25. [2H3-1.3-1] Trong không gian Oxyz , cho mặt cầu S : x 1 y2 z 1 9. Bán kính 
 của mặt cầu S là: 
 9
 A. 18. B. 9 . C. 3 . D. .
 2
Trang 3 Tổ 2 ĐỢT 14
Câu 26. [1H3-4.3-1] Cho hình lăng trụ tứ giác đều ABCD.A B C D có cạnh đáy bằng a , cạnh bên 
 bằng a 3 . Tính cosin góc giữa hai mặt phẳng ABCD và ABC :
 1 3
 A. 30 . B. . C. 60 . D. .
 2 2
 bx c
Câu 27. [2D1-5.1-1] Cho hàm số y ( a 0 và a,b,c ¡ ) có đồ thị như hình bên. Khẳng định 
 x a
 nào dưới đây đúng?
 A. a 0 , b 0 , c ab 0 . B. a 0 ,b 0 , c ab 0 .
 C. a 0 , b 0 , c ab 0 . D. a 0 , b 0 , c ab 0 .
Câu 28. [2D3-1.3-3] Cho F(x) (ax2 bx c)e2x là một nguyên hàm của hàm số 
 f (x) (2020x2 2022x 1)e2x trên khoảng ( ; ) . Tính T a 2b 4c .
 A. T 1012 . B. T 2012 . C. T 1004 . D. T 1018 .
 1 3
Câu 29. [2D3-1.1-2] Cho hàm số f x xác định trên ¡ \  thỏa mãn f ' x , f 0 1. Giá 
 3 3x 1
 trị của f 1 bằng:
 A. 3ln 2 3.B. 2ln 2 1.C. 3ln 2 4 .D. 12ln 2 3 .
Câu 30. [2H2-1.2-2] Cho hình nón có bán kính đáy bằng 3, chiều cao bằng 4. Tính diện tích xung quanh 
 của hình nón.
 A. 12 .B. 9 . C. 30 .D. 15 .
Câu 31. [1D1-3.1-2] Cho phương trình cos 2x sin x 1 0 (*) . Bằng cách đặt t sin x 1 t 1 thì 
 phương trình * trở thành phương trình nào sau đây? 
 A. 2t 2 t 0 . B. 2t 2 t 0 . C. 2t 2 t 0. D. 2t 2 t 2 0 .
Câu 32. [2D2-2.1-2] Tìm tập xác định D của hàm số y x2 6x 9 2
 A. D ¡ \ 0 . B. D 3; . C. D ¡ \ 3 . D. D ¡ .
Trang 4 Tổ 2 ĐỢT 14
Câu 33. [2D2-6.1-2] Tìm tập nghiệm S của bất phương trình ln x2 0 .
 A. S  1;1. B. S  1;0 . C. S  1;1 \ 0. D. S 0;1.
 1
Câu 34. [2D3-1.1-1] Tìm nguyên hàm của hàm số y . 
 3x 2
 1 1 1
 A. dx ln 3x 2 C . B. dx ln 3x 2 C .
 3x 2 3x 2 2
 1 1 1 1
 C. dx ln 3x 2 C . D. dx ln 2 3x C .
 3x 2 3 3x 2 3
Câu 35 . [2H2-1.4-3] Một cái cột có hình dạng như hình bên (gồm một khối nón và một khối trụ ghép 
 lại). Chiều cao đo được ghi trên hình, chu vi đáy là 20 3 cm. Thể tích của cột bằng:
 A. 13000 cm3 .B. 5000 cm3 .C. 15000 cm3 . D.52000 cm3 .
 log 2x 2 log x 3 2 2
Câu 36 . [2D2-5.2-3] Gọi S là tập nghiệm thực của phương trình 2 2 . Tổng 
 các phần tử của S bằng a b 2 (với a,b là các số nguyên). Giá trị của biểu thức Q a.b 
 bằng
 A. 6 .B. 0 .C. 8 . D. 4 .
 a 21
Câu 37. [2H1-3.2-2] Cho hình chóp tam giác đều có cạnh bên bằng và mặt bên tạo với mặt 
 3
 phẳng đáy một góc bằng 60o . Tính thể tích V của khối chóp.
 a3 3 a 3 7 21 a3 7 21
 A. V .B. V .C. V a 3 3 .D. V .
 3 32 96
Câu 38. [1H3-5.4-2] Cho tứ diện ABCD có AB 2 , các cạnh còn lại bằng 4, khoảng cách giữa hai 
 đường thẳng AB và CD bằng
 A. 13 .B. 3 . C. 2 .D. 11 .
Câu 39. [2D2-4.5-3] Trong năm 2020 (tính đến hết ngày 31/12/2020), diện tích rừng trồng mới của tỉnh 
 A là 1200ha . Giả sử diện tích rừng trồng mới của tỉnh A mỗi năm tiếp theo đều tăng 6% so 
 với diện tích rừng trồng mới của năm liền trước. Kể từ sau năm 2020, năm nào dưới đây là năm 
 đầu tiên tỉnh A có diện tích rừng trồng mới trong năm đó đạt trên 1600ha ?
 A. 2043. B. 2025 . C. 2024 . D. 2042 .
Câu 40. [2D3-1.2-3] Cho f 4x dx e2x x2 C . Khi đó f x dx bằng
 2x x x x 2
 e 2 1 2 1 2 x 
 A. 4x C . B. 4e 2 x C . C. 4e 2 x C . D. e 2 C .
 4 4 4 4 
Trang 5 Tổ 2 ĐỢT 14
Câu 41. [2D2-3.2-3] Gọi n là số nguyên dương sao cho 
 1 1 1 1 210
 ... đúng với mọi x dương, x 1 . Tính 
 log x log x log x log x log x
 2020 20202 20203 2020n 2020
 giá trị của biểu thức P 3n 4 .
 A. P 16 .B. P 61. C. P 46 .D. P 64 .
Câu 42. [2H2-2.2-3] Trong không gian cho hình chóp S.ABCD có đáy là hình thang vuông tại A và D 
 với AB AD 2 , CD 1, cạnh bên SA 2 và SA vuông góc với đáy.Gọi E là trung điểm 
 AB . Tính diện tích Smc của mặt cầu ngoại tiếp hình chóp S.BCE .
 14 14
 A. S 41 .B. S . C. S . D. S 14 .
 mc mc 4 mc 2 mc
 x
Câu 43 . [2D1-5.6-3] Cho hàm số y có đồ thị C . Gọi A, B x x là 2 điểm trên C mà 
 x 1 A B
 tiếp tuyến tại A, B song song với nhau và AB 2 2 . Tích của xA.xB bằng.
 A. 2 .B. 1. C. 0 . D. 2 .
Câu 44. [2D1-3.6-3] Bác thợ hàn dùng một thanh kim loại 4m để uốn thành khung cửa sổ có dạng như 
 hình vẽ. Gọi r là bán kính của nửa đường tròn, tìm r (theo mét) để diện tích tạo thành đạt giá 
 trị lớn nhất.
 4 2
 A.1m .B. 0,5m . C. m.D. m
 4 4 
Câu 45. [2H1-3.2-3] Cho hình lăng trụ ABC.A' B 'C 'có AA' 2 13a ,tam giác ABC vuông tại C và góc
 ABC 300 , góc giữa cạnh bên CC 'và mặt phẳng ABC bằng 600 . Hình chiếu vuông góc 
 của B ' lên mặt phẳng ABC là trọng tâm của tam giác ABC . Thể tích của khối tứ diện 
 A'.ABC theo a bằng
 33 39a3 9 13a3 99 13a3 27 13a3
 A. .B. . C. . D. .
 4 2 8 2
Trang 6 Tổ 2 ĐỢT 14
 x 1 x x 1
Câu 46. [2D2-5.5-3] Cho hai hàm số y và y e x 2021 3m ( m là tham số thực) 
 x x 1 x 2
 có đồ thị lần lượt là C1 và C2 . Có bao nhiêu số nguyên m thuộc 2021;2020 để C1 và
 C2 cắt nhau tại 3 điểm phân biệt ?
 A. 2694 .B. 2693. C. 4041. D. 4042 .
Câu 47. [2D2-6.5-3] Cho hàm số y f (x) . Hàm số y f , (x) có bảng biến thiên như sau :
 2
 Bất phương trình f (x) ex m đúng với mọi x ( 1;1) khi và chỉ khi
 A. m f ( 1) e . B. m f (0) 1. C. m f (0) 1. D. m f ( 1) e .
Câu 48. [2H1-3.6-4] Cho hình chóp S.ABCD có đáy ABCD là hình bình hành và có thể tích là V . Gọi 
 SM 1
 M là điểm thuộc cạnh SC sao cho . Mặt phẳng chứa AM và cắt hai cạnh 
 SC 3
 SB, SD lần lượt tại P và Q . Gọi V , là thể tích của khối chóp 
 SP SQ V ,
 S.APMQ; x; y; (0 x; y 1) . Khi tỉ số đạt giá trị nhỏ nhất,tìm giá trị của tổng 
 SB SD V
 x 3y
 1 1
 A. 2 . B. . C. 1. D. .
 6 2
Câu 49. [1D2-5.5-4] Tổ 1 của một lớp học có 13 học sinh gồm 8 học sinh nam trong đó có bạn A, và 5 
 học sinh nữ trong đó có bạn B được xếp ngẫu nhiên vào 13 ghế trên một hàng ngang để dự lễ sơ 
 kết học kỳ 1. Tính xác suất để xếp được giữa hai bạn nữ gần nhau có đúng hai bạn nam, đồng 
 thời bạn A không ngồi cạnh bạn B.
 4 1 4 1
 A. . B. .C. . D. .
 6453 1287 6435 1278
Câu 50. [2D1-2.2-4] Cho hàm số F x có F 0 0 . Biết y F x là một nguyên hàm của hàm số 
 y f x đồ thị như hình vẽ. Số điểm cực trị của hàm số G x F x6 x3 là
 A. 4 .B. 5 . C. 6 . D.3 .
 --------- HẾT--------
Trang 7 Tổ 2 ĐỢT 14
 HƯỚNG DẪN GIẢI
 BẢNG ĐÁP ÁN
 1.C 2.D 3.A 4.A 5.A 6.B 7.D 8.D 9.D 10.B
 11.B 12.D 13.D 14.C 15.A 16.A 17.C 18.C 19.A 20.A
 21.B 22.A 23.D 24.C 25.C 26.B 27.B 28.A 29.B 30.D
 31.B 32.C 33.C 34.C 35.A 36.D 37.A 38.D 39.B 40.C
 41.D 42.D 43.C 44.C 45.B 46.B 47.B 48.A 49.C 50.D
Câu 1. [2H1-1.1-1] Hình nào dưới đây không phải là hình đa diện? 
 A. B. C. D. 
 Lời giải
 FB tác giả: Đoàn Nguyệt 
 - Khái niệm hình đa diện: là hình được tạo bởi một số hữu hạn các đa giác thỏa mãn hai tính 
 chất sau: 
 1) Hai đa giác phân biệt chỉ có thể hoặc không có điểm chung, hoặc chỉ có một đỉnh chung, 
 hoặc chỉ có một cạnh chung. 
 2) Mỗi cạnh của đa giác nào cũng là cạnh chung của đúng hai đa giác.
 Quan sát 4 hình vẽ, hình C có cạnh màu đỏ không thỏa mãn tính chất số 2. 
Câu 2. [2D1-1.5-1] Cho hàm số f (x) nghịch biến trên K . Mệnh đề nào sau đây đúng? 
 f (x1)
 A. 1 với mọi x1, x2 K và x1 x2.
 f (x2 )
 f (x2 ) f (x1)
 B. 0 với mọi x1, x2 K và x1 x2 .
 x2 x1
 C. f (x1) f (x2 ) với mọi x1, x2 K và x1 x2.
 f (x2 ) f (x1)
 D. 0 với mọi x1, x2 K và x1 x2 .
 x2 x1
 Lời giải
Trang 8 Tổ 2 ĐỢT 14
 FB tác giả: Đoàn Nguyệt 
 Với x1, x2 K và x1 x2 , không mất tính tổng quát ta giả sử x1 x2 . 
 Do x1 x2 và hàm số f (x) nghịch biến trên K nên f x1 f x2 f x2 f x1 0 .
 f (x2 ) f (x1)
 Suy ra 0 với mọi x1, x2 K và x1 x2 .
 x2 x1
 2x 3
Câu 3. [2D1-5.4-1] Tọa độ giao điểm M của đồ thị hàm số y với trục hoành là
 x 2
 3 3 
 A. ;0 . B. 2;0 .C. 0; 2 . D. 0; .
 2 2 
 Lời giải
 FB tác giả: huong vu 
 2x 3 3
 Cho 0 x 
 x 2 2
 3 
 Vậy M ; 0 
 2 
Câu 4. [2D1-4.1-1] Cho hàm số y f (x) có đạo hàm trên R \ 1 và có bảng biến thiên
 Tổng số tiệm cận ngang và tiệm cận đứng của đồ thị hàm số đã cho là
 A.3 B. 1 C. 4 D. 2
 Lời giải
 FB tác giả: huong vu 
 Ta có lim y 5 suy ra y 5 là 1 tiệm cận ngang
 x 
 lim y 2 suy ra y 2 là 1 tiệm cận ngang
 x 
 lim y suy ra x 1 là 1 tiệm cận đứng
 x 1 
 Vậy đồ thị hàm số có 3 tiệm cận ngang và tiệm cận đứng.
Câu 5. [2D3-1.1-1] Họ các nguyên hàm của hàm số f x 5x x là 
 5x x2 x2 5x
 A. C . B. 5x x2 C . C. 5x ln 2 C . D. 1 C .
 ln5 2 2 ln5
 Lời giải
 FB tác giả: Nguyễn Trung Việt 
 5x x2
 5x x dx C .
 ln5 2
Trang 9 Tổ 2 ĐỢT 14
  
Câu 6. [2H3-1.1-1] Trong không gian Oxyz , cho hai điểm A 1;1; 1 và B 2;3;2 . Tọa độ vectơ AB
 là 
 A. 1; 2; 3 . B. 1;2;3 . C. 3;4;1 . D. 1;2;1 .
 Lời giải
 FB tác giả: Nguyễn Trung Việt 
  
 AB xB xA ; yB yA ; zB zA 1;2;3 .
Câu 7. [2H1-3.2-1] Cho khối chóp S.ABCD có đáy ABCD là hình vuông cạnh 1. Biết SA vuông góc 
 với ABCD và SA 3 . Thể tích của khối chóp S.ABCD là:
 1 3 3
 A. . B. 3 . C. . D. .
 4 6 3
 Lời giải
 FB tác giả: Hiếu Nguyễn
 S
 A
 D
 B C
 2
 SABCD 1 1
 1 1 1 3
 V .S .h .S .SA .1. 3 
 S.ABCD 3 ABCD 3 ABCD 3 3
Câu 8. [2D1-5.6-1] Cho hàm số y x3 2x 1có đồ thị C . Hệ số góc của tiếp tuyến với C tại 
 điểm M 1;2 bằng:
 A. 3 . B. 5 . C. 25 . D. 1.
 Lời giải
 FB tác giả: Hiếu Nguyễn
 Yêu cầu cần đạt: Thuộc công thức phương trình tiếp tuyến tại điểm của hàm số.
 y x3 2x 1
 y ' 3x2 2
 k y ' 1 3. 1 2 2 1
 3
Câu 9. [2D2-1.2-1] Cho biểu thức P x 4 . x5 , x 0 . Khẳng định nào sau đây là đúng.
 1 1
 A. P x2 . B. P x 2 . C. P x 2 . D. P x 2 .
 Lời giải
Trang 10