Đề minh họa tốt nghiệp THPT môn Khối 12 - Năm học 2020-2021 (Có đáp án)

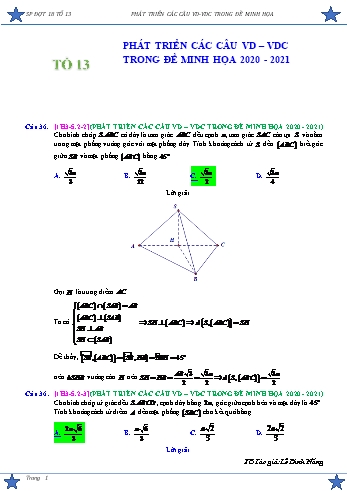
 SP ĐỢT 18 TỔ 13 PHÁT TRIỂN CÁC CÂU VD-VDC TRONG ĐỀ MINH HỌA 
 PHÁT TRIỂN CÁC CÂU VD – VDC
 TỔ 13 TRONG ĐỀ MINH HỌA 2020 - 2021
Cõu 36. [1H3-5.2-2] (PHÁT TRIỂN CÁC CÂU VD – VDC TRONG ĐỀ MINH HỌA 2020 - 2021) 
 Cho hỡnh chúp S.ABC cú đỏy là tam giỏc ABC đều cạnh a , tam giỏc SAC cõn tại S và nằm 
 trong mặt phẳng vuụng gúc với mặt phẳng đỏy. Tớnh khoảng cỏch từ S đến ABC biết gúc 
 giữa SB và mặt phẳng ABC bằng 45.
 3a 3a 3a 3a
 A. .B. . C. . D. .
 3 12 2 4
 Lời giải
 Gọi H là trung điểm AC . 
 ABC  SAB AB
 ABC  SAB 
 Ta cú SH  ABC d S, ABC SH .
 SH  AB
 SH  SAB 
 Dễ thấy, ãSB, ABC ãSB, HB Sã BH 45 
 AB 3 3a 3a
 nờn SHB vuụng cõn H nờn SH HB d S, ABC .
 2 2 2
Cõu 36 . [1H3-5.2-3] (PHÁT TRIỂN CÁC CÂU VD – VDC TRONG ĐỀ MINH HỌA 2020 - 2021) 
 Cho hỡnh chúp tứ giỏc đều S.ABCD , cạnh đỏy bằng 2a , gúc giữa cạnh bờn và mặt đỏy là 45. 
 Tớnh khoảng cỏch từ điểm A đến mặt phẳng SBC cho kết quả bằng 
 2a 6 a 6 a 2 2a 2
 A. . B. . C. . D. .
 3 3 3 3
 Lời giải
 FB Tỏc giả: Lờ Đỡnh Năng 
 Trang 1 SP ĐỢT 18 TỔ 13 PHÁT TRIỂN CÁC CÂU VD-VDC TRONG ĐỀ MINH HỌA 
 S
 H
 A B
 2a
 M
 O
 D C
 Gọi O AC  BD khi đú O là tõm của đỏy và ta cú SO  ABCD tại O .
 Gúc giữa cạnh bờn và mặt đỏy bằng 45 Sã AO 45 ΔSAO vuụng cõn tại O .
 AC
 Ta cú AC 2a 2 AO a 2 SO a 2 .
 2
 d A, SBC AC
 Cú AO  SBC C 2 d A, SBC 2d O, SBC .
 d O, SBC OC
 Gọi M là trung điểm của BC OM là đường trung bỡnh của ΔCAB OM // AB
 Mà AB  BC OM  BC ; lại cú SO  BC (do SO  ABCD , BC  ABCD )
 BC  SOM SOM  SBC ; cú SOM  SBC SM ; kẻ OH  SM tại H
 OH  SBC tại H d O, SBC OH .
 Ta cú OM a , tam giỏc SOM vuụng tại O đường cao OH
 1 1 1 3 a 6 2a 6
 OH d A, SBC .
 OH 2 SO2 OM 2 2a2 3 3
Cõu 37. [2H3-1.3-2] (PHÁT TRIỂN CÁC CÂU VD – VDC TRONG ĐỀ MINH HỌA 2020 - 2021) 
 Trong khụng gian Oxyz , phương trỡnh mặt cầu cú tõm là I 1;2; 3 và tiếp xỳc với 
 P : x 2y 2z 7 0 là
 A. x 1 2 y 2 2 z 3 2 36 .B. x 1 2 x 2 2 z 3 2 6 .
 C. x2 y2 z2 2x 4y 6z 22 0 .D. x2 y2 z2 2x 4y 6z 8 0 .
 Lời giải
 Fb: Nghĩa Nguyễn
 Ta cú bỏn kớnh mặt cầu cần tỡm là R d I; P 6
 Phương trỡnh mặt cầu cần tỡm là : x 1 2 y 2 2 z 3 2 36
 x2 y2 z2 2x 4y 6z 22 0.
vannhacaohmu@gmail.com
 Trang 2 SP ĐỢT 18 TỔ 13 PHÁT TRIỂN CÁC CÂU VD-VDC TRONG ĐỀ MINH HỌA 
Cõu 37. [2H3-1.3-2] (PHÁT TRIỂN CÁC CÂU VD – VDC TRONG ĐỀ MINH HỌA 2020 - 2021) 
 Trong khụng gian Oxyz , cho hai điểm A 2;4;1 , B 2;2; 3 . Phương trỡnh mặt cầu đường 
 kớnh AB 
 2 2 2 2
 A. x2 y 3 z 1 36. B. x2 y 3 z 1 9.
 2 2 2 2
 C. x2 y 3 z 1 9. D. x2 y 3 z 1 36.
 Lời giải
 FB tỏc giả: Phong Nha 
 Gọi I là trung điểm của AB I(0;3; 1).
  
 IA (2;1;2) IA 22 12 22 3.
 2 2
 Mặt cầu đó cho cú tõm I , đường kớnh AB nờn cú phương trỡnh là x2 y 3 z 1 9.
Cõu 38. [2H3-3.2-1] (PHÁT TRIỂN CÁC CÂU VD – VDC TRONG ĐỀ MINH HỌA 2020 - 2021) 
 Trong khụng gian Oxyz , đường thẳng đi qua hai điểm M 2;0;1 và N 3; 1; 2 cú phương 
 trỡnh chớnh tắc là
 x 2 y z 1 x 2 y z 1
 A. .B. .
 5 1 3 5 1 3
 x 3 y 1 z 2 x 3 y 1 z 2
 C. .D. .
 5 1 3 5 1 3
 Lời giải
 Fb:Nguyễn Thị Thựy Nương
 Chọn B
  
 Ta cú đường thẳng đi qua hai điểm M 2;0;1 và N 3; 1; 2 cú VTCP MN 5; 1; 3 cú 
 x 2 y z 1
 phương trỡnh chớnh tắc là .
 5 1 3
Cõu 38: [2H3-3.2-1] (PHÁT TRIỂN CÁC CÂU VD – VDC TRONG ĐỀ MINH HỌA 2020 - 2021) 
 Trong khụng gian Oxyz , cho tam giỏc ABC cú A 1;3; 2 , B 2;0;5 ,C 0; 2;1 . Phương 
 trỡnh đường trung tuyến AM của tam giỏc ABC là 
 x 1 y 3 z 2 x 1 y 1 z 3
 A. . B. .
 2 4 5 3 5 8
 x 1 y 3 z 2 x 2 y 4 z 5
 C. . D. .
 2 4 5 1 3 2
 Lời giải
 FB tỏc giả: Nguyễn Văn Rin
 Do M là trung điểm BC nờn M 1; 1; 3 .
  
 Vectơ chỉ phương của đường thẳng AM là u AM 2; 4;5 .
 Đường trung tuyến AM đi qua A 1;3; 2 và cú VTCP u 2; 4;5 cú phương trỡnh là 
 x 1 y 3 z 2
 .
 2 4 5
 Trang 3 SP ĐỢT 18 TỔ 13 PHÁT TRIỂN CÁC CÂU VD-VDC TRONG ĐỀ MINH HỌA 
Cõu 39. [2D1-3.1-2] (PHÁT TRIỂN CÁC CÂU VD – VDC TRONG ĐỀ MINH HỌA 2020 - 2021) 
 Cho hàm số y f x , đồ thị hàm số y f ' x là đường cong trong hỡnh vẽ bờn. 
 1 1 
 Giỏ trị nhỏ nhất của hàm số g x f 4x 4x trờn đoạn ; bằng
 4 2 
 A. f 2 2 B. f 1 1.
 C. f 0 D. f 2 2 .
 Lời giải
 FB tỏc giả: Phan Quang Sơn 
 1 1 
 +) Xột hàm số g x f 4x 4x trờn đoạn ; . Ta cú g ' x 4 f ' 4x 4 .
 4 2 
 +) Từ đồ thị của hàm số y f ' x và đồ thị của y 1 ta cú: 
 g ' x 0 f ' 4x 1
 x 0
 4x 0 
 a 1 .
 4x a 2 x 
 4 2
 Bảng biến thiờn của hàm số g x f 4x 4x
 Dựa vào bảng biến thiờn ta cú Ming x f 2 2 .
 1 1 
 ;
 4 2 
Cõu 39. [2D1-3.2-3] (PHÁT TRIỂN CÁC CÂU VD – VDC TRONG ĐỀ MINH HỌA 2020 - 2021) 
 Cho hàm số y = f (x), đồ thị của hàm số y = f '(x) là đường cong như hỡnh bờn dưới
 Trang 4 SP ĐỢT 18 TỔ 13 PHÁT TRIỂN CÁC CÂU VD-VDC TRONG ĐỀ MINH HỌA 
 y
 O x
 Giỏ trị nhỏ nhất của hàm số g(x)= f (2x + 3) + 2x2 + 6x- 5 bằng
 A. f ( 3) 9 . B. f (1) 3. C. f ( 1) 9 . D. f (3) 5 .
 Lời giải
 FB tỏc giả: Lờ Bỡnh 
 g(x)= f (2x + 3) + 2x2 + 6x- 5 .
 Ta cú gÂ(x)= 2 f Â(2x + 3) + 4x + 6
 gÂ(x)= 0 Û 2 f Â(2x + 3) = - 4x- 6 Û f Â(2x + 3) = - (2x + 3)
 Đặt t = 2x + 3 khi đú ta được (1): f Â(t) = - t.
 (1) là phương trỡnh hoành độ giao điểm của đồ thị hàm số y = f Â(t) và đường thẳng d : y = - t
 (hỡnh vẽ)
 y
 y t
 O x
 Dựa vào đồ thị hàm số y = f Â(t) và đường thẳng d : y = - t ta cú 
 ột = - 3 ộx = - 3
 ờ ờ
 f Â(t) = - t.Û ờt = - 1 hay ờx = - 2
 ờ ờ
 ờ ờ
 ởt = 1 ởx = - 1
 Bảng biến thiờn của hàm số g(x)
Trang 5 SP ĐỢT 18 TỔ 13 PHÁT TRIỂN CÁC CÂU VD-VDC TRONG ĐỀ MINH HỌA 
 Dựa vào bảng biến thiờn ta cú giỏ trị nhỏ nhất của hàm số g(x) bằng f ( 1) 9
Cõu 40. [2D2-6.5-3] (PHÁT TRIỂN CÁC CÂU VD – VDC TRONG ĐỀ MINH HỌA 2020 - 2021) 
 Cú bao nhiờu số nguyờn dương y sao cho ứng với mỗi y cú khụng quỏ 8 số nguyờn x thỏa 
 món 
 (5 x+ 2 - 5).(5 x - 4 y)< 0 ?
 A. 97656 .B. 488281.C. 39066 .D. 19531. 
 Lời giải
 FB tỏc giả : Quang Thành Phạm
 Ta cú : (5 x+ 2 - 5).(5 x - 4 y)< 0 Û (25.5 x - 5).(5 x - 4 y)< 0
 ổ 5 ử ổ 5 ử
 ỗ x ữ x ỗ x ữ x
 Û 25.ỗ5 - ữ.(5 - 4 y)< 0 Û ỗ5 - ữ.(5 - 4 y)< 0
 ốỗ 25 ứữ ốỗ 25 ứữ
 5 ổ 5 ử
 ỗ x ữ x
 Vỡ y ³ 1ị 4y > ị ỗ5 - ữ> (5 - 4y) 
 25 ốỗ 25 ứữ
 ùỡ ỡ
 ù x 5 ù 3
 ù 5 - > 0 ù x > - 3
 Khi đú ta được : ớ 25 Û ớ 2 Û - < x < log (4y)
 ù ù 2 5
 ù x ù x < log (4y)
 ợù 5 - 4y < 0 ợù 5
 7
 Do mỗi y cú khụng quỏ 8 số nguyờn x nờn log5 (4y) Ê 7 ị 4 y Ê 5 ị y Ê 19531,25
 Như vậy cú 19531 giỏ trị y nguyờn dương thỏa món
Cõu 40: [2D2-6.3-3] (PHÁT TRIỂN CÁC CÂU VD – VDC TRONG ĐỀ MINH HỌA 2020 - 2021) 
 Cú bao nhiờu số nguyờn dương y sao cho ứng với mỗi y cú khụng qua 8 số nguyờn x thỏa 
 món 3x 1 3 3x y 1 0 
 A. 6562 . B. 6563. C. 6561. D. 6574 .
 Lời giải
 FB tỏc giả: Hanh Nguyờn
 Đặt t 3x 0
 Theo bài ra ta cú bất phương trỡnh: 3t 3 t y 1 0 * 
 TH 1. 
 3
 3t 3 0 t 3 3 3
 * 3 t y 1 y 1 nờn y 1 , 
 t y 1 0 3 3 3
 t y 1
 Trang 6 SP ĐỢT 18 TỔ 13 PHÁT TRIỂN CÁC CÂU VD-VDC TRONG ĐỀ MINH HỌA 
 1 1
 Mặt khỏc 3x y 1 x log y 1 .
 3 2 3
 Nếu log3 y 1 8 thỡ x 0;1;2;3;4;5;6;7;8 đều là nghiệm, nờn khụng thỏa món.
 8
 Suy ra log3 y 1 8 y 1 3 y 6562 . Vậy y 2;3;...;6562.
 TH 2. 
 3
 3t 3 0 t 3 3 3
 * 3 y 1 t y 1 y 1 .
 t y 1 0 3 3 3
 t y 1
 3 3
 Vỡ y  nờn xột y 1. Khi đú ta cú 0 t 0 3x Khụng cú giỏ trị x thỏa 
 3 3
 món yờu cầu bài toỏn.
 Kết luận: Cú 6561 số y thỏa món yờu cầu bài toỏn.
Cõu 41. [2D3-2.2-3] (PHÁT TRIỂN CÁC CÂU VD – VDC TRONG ĐỀ MINH HỌA 2020 - 2021) 
 3x 2x3 khi x 2
 Cho hàm số f x . 
 4 3x khi x 2
 0
 Tớch phõn f 1 2sin 2x .cos 2x.dx bằng:
 4
 1 1 47 1
 A. . B. . C. . D. .
 8 4 8 8
 Lời giải
 FB tỏc giả: Võn Nguyễn 
 du
 Đặt u 1 2sin 2x du 4cos 2x.dx cos 2x.dx .
 4
 Với x u 3 .
 4
 Với x 0 u 1.
 0 1 du 1 2 1 
 f 1 2sin 2x .cos 2x.dx f u . f u .du f u .du 
 4 4
 3 3 2 
 4
 2 1
 1 3 1 23 1
 4 3u .du 3u 2u .du 12 .
 4 3 2 4 2 8
Cõu 41. [2D3-2.2-3](PHÁT TRIỂN CÁC CÂU VD – VDC TRONG ĐỀ MINH HỌA 2020 - 2021) 
 2x 1 khi x 0 2
 Cho hàm số f x . Tớch phõn sin 2x f sin x dx bằng 
 2 
 x x 1 khi x 0 
 2
 13 5 19 11
 A. . B. . C. . D. .
 3 3 3 3
 Lời giải
 Trang 7 SP ĐỢT 18 TỔ 13 PHÁT TRIỂN CÁC CÂU VD-VDC TRONG ĐỀ MINH HỌA 
 FB tỏc giả: Chuc Nguyen 
 2 2
 Ta cú I sin 2x f sin x dx 2sin x f sin x cos xdx 
 2 2
 2
 2 sin x d f sin x 
 2
 2
 2
 2sin x f sin x 2 f sin x cos x dx 
 2 
 2
 2 f 1 2 f 1 I1
 2
 Ta cú: f 1 21 1 1; f 1 1 1 1 1.
 2
 Tớnh I 2 f sin x cos x dx .
 1 
 2
 Đặt sin x t . Suy ra 
 1 0 1 0 1 1
 I 2 f t dt 2 f t dt 2 f t dt 2 t 2 t 1 dt 2 2t 1 dt .
 1 
 1 1 0 1 0 3
 1 13
 Do vậy I 2 1 1 . 
 3 3
Cõu 42. [2D4-3.3-3] (PHÁT TRIỂN CÁC CÂU VD – VDC TRONG ĐỀ MINH HỌA 2020 - 2021) 
 Biết rằng cú hai số phức thỏa món 2 z i z z 2i và 2 z i z là số thực. Tớnh tổng cỏc 
 phần ảo của hai số phức đú 
 A. 9. B. 7. C. 5. D. 3.
 Lời giải
 FB tỏc giả: Thuy Nguyen 
 Đặt z a bi, a,b Ă ta cú: 
 2 z i z z 2i
 2 a bi i 2bi 2i
 4 a2 b 1 2 4 b 1 2
 a2 b2 2b 1 b2 2b 1 a2 4b (1)
 Lại cú
 2 z i z 2 a bi i a bi 
 2 a bi a 1 b i 
 a(2 a) b(1 b) (2 a)(1 b) abi
 Là số thực nờn phần ảo của nú (2 a)(1 b) ab 0 2 a 2b 0 (2)
 Trang 8 SP ĐỢT 18 TỔ 13 PHÁT TRIỂN CÁC CÂU VD-VDC TRONG ĐỀ MINH HỌA 
 a2 a 1 5
 Thay 1 vào 2 ta cú: 2 a 2. 0 a2 2a 4 0 .
 4 a 1 5
 3 5
 Với a 1 5 b .
 2
 3 5
 Với a 1 5 b .
 2
 Vậy tổng phần ảo của hai số phức đú là 3 .
Cõu 42. [2D4-3.3-3] (PHÁT TRIỂN CÁC CÂU VD – VDC TRONG ĐỀ MINH HỌA 2020 - 2021) 
 Cho số phức z x yi, x, y Ă , với y 1 thỏa món z 2 và z 1 i 2 z z 2i 
 a 5 b
 thỡ x a, b Ă . Khi đú 2a b 333 bằng 
 52
 A. 2023. B. 256 . C. 2021.D. 238 .
 Lời giải
 FB tỏc giả: Kim Anh 
  Ta cú z 2 x2 y2 4 1 .
  z 1 i 2 z z 2i x y 2 x y i x2 y2 2y 2xi .
 2
 x y 2 2 x y 2 x2 y2 2y 4x2 2 .
  Thay 1 vào 2 ta được x y 2 2 x y 2 4 2y 2 4x2 .
 x2 y2 4 2xy 4x 4y x2 y2 2xy 4y2 16y 16 4x2 3 .
 Thay 1 vào 3 ta được 4 4 4x 4y 4 16y 32 x 5y 5 4 .
 x 5y 5 26y2 50y 21 0 5 
 Từ 4 và 1 ta cú .
 2 2 
 x y 4 x 5y 5
 25 79
 y 
 26
 Ta cú 5 .
 25 79
 y 
 26
 25 79
 y 
 26
  Do y 1 nờn .
 5 5 79
 x 
 26
 a 5 b
 Mà x a, b Ă nờn a 10, b 316 2a b 333 3.
 52 
Cõu 43. [2H1-3.2-2] (PHÁT TRIỂN CÁC CÂU VD – VDC TRONG ĐỀ MINH HỌA 2020 - 2021) 
 Cho hỡnh chúp S.ABC cú đỏy là tam giỏc ABC vuụng tại A và AB 3a, BC 5a . Cạnh bờn 
 SA vuụng gúc với mặt phẳng đỏy, gúc giữa đường thẳng SA và mặt phẳng SBC bằng 30 
 (tham khảo hỡnh bờn). Thể tớch của khối chúp S.ABC bằng 
 Trang 9 SP ĐỢT 18 TỔ 13 PHÁT TRIỂN CÁC CÂU VD-VDC TRONG ĐỀ MINH HỌA 
 8 3a3 24 3a3 48 3a3
 A. .B. . C. 5 3a3 . D. .
 5 5 5
 Lời giải
 FB tỏc giả: Thu Pham
 Gọi AH là đường cao của tam giỏc ABC và AI là đường cao của tam giỏc SAH .
 Vỡ SA  ABC nờn SA  BC . 
 SA  BC
 Ta cú BC  SAH mà AI  SAH AI  BC . 
 AH  BC 
 AI  BC
 Ta cú AI  SBC . 
 AI  SH
 ã
 Ta cú SI là hỡnh chiếu của SA lờn mặt phẳng SBC nờn ASI là gúc giữa đường thẳng SA và 
 mặt phẳng SBC . 
 AB.AC 3a.4a 12a
 Cú AC BC 2 AB2 25a2 9a2 4a , AH .
 BC 5a 5
 AH AH 12 3a
 tan ãASH SA .
 SA tan 30 5
 1 1
 S AB.AC .3a.4a 6a2.
 ABC 2 2
Trang 10