Đề kiểm tra giữa học kỳ II môn Toán Lớp 12 - Năm học 2020-2021 (Có đáp án)

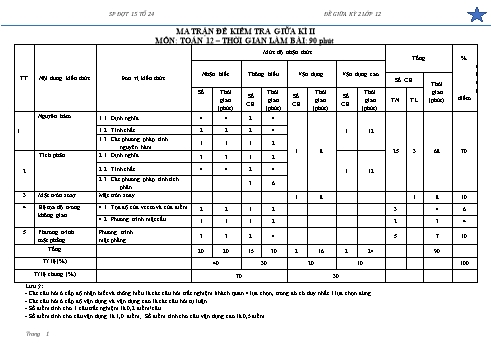
 SP ĐỢT 15 TỔ 24 ĐỀ GIỮA KỲ 2 LỚP 12
 MA TRẬN ĐỀ KIỂM TRA GIỮA KÌ II
 MÔN: TOÁN 12 – THỜI GIAN LÀM BÀI: 90 phút
 Mức độ nhận thức
 Tổng % 
 t
 Nhận biết Thông hiểu Vận dụng Vận dụng cao ổ
 TT Nội dung kiến thức Đơn vị kiến thức Số CH
 Thời n
 Số Thời Thời Thời Thời gian g
 Số Số Số 
 Cgian gian gian gian TN TL (phút) điểm
 CH CH CH
 H(phút) (phút) (phút) (phút)
 Nguyên hàm 1.1. Định nghĩa 4 4 2 4
1 1.2. Tính chất 2 2 2 4 1 12
 1.3. Các phương pháp tính 
 1 1 1 2
 nguyên hàm
 1 8 25 3 68 70
 Tích phân 2.1. Định nghĩa 3 3 1 2
 2 2.2. Tính chất 4 4 2 4 1 12
 2.3. Các phương pháp tính tích 
 3 6
 phân
 3 Mặt tròn xoay Mặt tròn xoay 1 8 1 8 10
 4 Hệ tọa độ trong 4.1. Tọa độ của vectơ và của điểm 2 2 1 2 3 4 6
 không gian
 4.2. Phương trình mặt cầu 1 1 1 2 2 3 4
 5 Phương trình Phương trình 
 3 3 2 4 5 7 10
 mặt phẳng mặt phẳng
 Tổng 20 20 15 30 2 16 2 24 90
 Tỉ lệ (%) 40 30 20 10 100
 Tỉ lệ chung (%) 70 30
 Lưu ý:
 - Các câu hỏi ở cấp độ nhận biết và thông hiểu là các câu hỏi trắc nghiệm khách quan 4 lựa chọn, trong đó có duy nhất 1 lựa chọn đúng.
 - Các câu hỏi ở cấp độ vận dụng và vận dụng cao là các câu hỏi tự luận.
 - Số điểm tính cho 1 câu trắc nghiệm là 0,2 điểm/câu
 - Số điểm tính cho câu vận dụng là 1,0 điểm; Số điểm tính cho câu vận dụng cao là 0,5 điểm.
 Trang 1 SP ĐỢT 15 TỔ 24 ĐỀ GIỮA KỲ 2 LỚP 12
 ĐỀ KIỂM TRA GIỮA HỌC KỲ II LỚP 12 
 NĂM HỌC 2020 – 2021
 TỔ 24 MÔN TOÁN
 THỜI GIAN: 90 PHÚT
A. PHẦN TRẮC NGHIỆM (7 ĐIỂM)
Câu 1. [2D3-1.1-1] Khẳng định nào sau đây là khẳng định đúng? 
 3
 A. 3x2dx 6x C . B. 3x2dx 9x3 C . C. 3x2dx x C . D. 3x2dx x3 C .
 2 
Câu 2. [2D3-1.1-1] Hàm số y F x là một nguyên hàm của hàm số y f x . Hãy chọn khẳng 
 định đúng.
 A. F x f x .B. F x f x . C. F x f x C . D. F x C f x .
Câu 3. [2D3-1.1-1] Cho f x , g x là các hàm số xác định và liên tục trên ¡ . Trong các mệnh đề 
 sau, mệnh đề nào sai?
 A. f x g x dx f x dx. g x dx .
 B. 5 f x dx 5 f x dx .
 C. f x 3g x dx f x dx 3 g x dx .
 D. f x g x dx f x dx g x dx .
Câu 4. [2D3-1.1-1] Trong các khẳng định sau, khẳng định nào sai?
 A. sin xdx cos x C . B. cos xdx sin x C . 
 C. 2xdx x2 C . D. exdx ex C .
Câu 5. [2D3-1.1-2] Tìm giá trị của m để hàm số F x m2 x3 3m 2 x2 4x 3 là một nguyên 
 hàm của hàm số f x 3x2 10x 4.
 A. m 1. B. m 2 . C. m 1. D. m 1.
Câu 6. [2D3-1.1-2] Giả sử hàm số F x là một nguyên hàm của hàm số f x trên K . Khẳng định 
 nào sau đây đúng.
 A. Chỉ có duy nhất một hằng số C sao cho hàm số y F(x) C là một nguyên hàm của hàm 
 f trên K.
 B. Chỉ có duy nhất hàm số y F(x) là nguyên hàm của f trên K.
 C. Với mỗi nguyên hàm G của f trên K thì tồn tại một hằng số C sao cho G(x) F(x) C 
 với x thuộc K .
 D. Với mỗi nguyên hàm G của f trên K thì G(x) F(x) C với mọi x thuộc K và C bất 
 kỳ.
Câu 7. [2D3-1.1-1] Mệnh đề nào sau đây sai ?
 A. Nếu f x dx F x C thì f t dt F t C .
 Trang 2 SP ĐỢT 15 TỔ 24 ĐỀ GIỮA KỲ 2 LỚP 12
 B. kf x dx k f x dx ( k là hằng số và k 0).
 C. f x dx f x C .
 D. f x f x dx f x dx f x dx .
 1 2 1 2 
Câu 8. [2D3-1.1-1] Cho hàm số f x xác định trên K . Chọn đẳng thức đúng? 
 A. f x dx f ' x C . B. f x g x dx f x dx g x dx .
 1
 C. kf x dx f x dx, k 0. D. f x .g x dx f x dx. g x dx .
 k 
 2021 1
Câu 9. [2D3-1.1-2] Tìm nguyên hàm của hàm số f x trên khoảng ;0 . 
 x x2
 1 1
 A. 2021.ln x C . B. 2021.ln x C .
 x x
 1 1
 C. 2021.ln x C . D. 2021.ln x C .
 x x
Câu 10. [2D3-1.1-2] Cho các hàm số y f (x) và y g(x) liên tục trên ¡ . Có bao nhiêu khẳng định 
 đúng trong các khẳng định sau?
 I. f (x)dx f (x) C .
 II. f (x)dx f (x) .
 III. k. f (x)dx k. f (x)dx (với k là hằng số).
 IV.  f (x) g(x)dx f (x)dx  g(x)dx .
 A. 0. B. 1. C. 2. D. 3.
Câu 11. [2D3-1.3-1] Hàm số f x x 2 ex có họ nguyên hàm là
 A. x 2 ex C .B. xex C .C. x 1 ex C . D. x 3 ex C .
Câu 12. [2D3-1.3-2] Cho hàm số f (x) (2x 1)e2x (x ¡ ) . Gọi F(x) là một nguyên hàm của f (x) 
 trên ¡ . Biết F(x) được viết dưới dạng F(x) (a.x b).em.x C , (a, b, m ¥ ) . Tính 
 T a b m .
 A. 12. B. 7. C. 4.D. 3.
Câu 13. [2D3-2.1-1] Cho hàm số f x liên tục trên 0;1 và f 1 f 0 2 . Tính tích phân 
 1
 I f x dx .
 0
 A. I 1. B. I 1. C. I 2 . D. I 0 .
 2020
Câu 14. [2D3-2.1-1] Tính tích phân I 7xdx . 
 0
 72020 1 72021
 A. I .B. I 72020 ln 7 .C. I 7 . D. I 2020.72019 .
 ln 7 2021
Câu 15. [2D3-1.1-1] Tìm nguyên hàm F x 2dx . 
 3 2 x2
 A. F x 2 x C . B. F x 2 x C . C. F x C . D. F x C .
 3 2
 Trang 3 SP ĐỢT 15 TỔ 24 ĐỀ GIỮA KỲ 2 LỚP 12
 1 ea 1
Câu 16. [2D3-2.1-2] Biết e4xdx với a,b ¢ ;b 0 . Tìm khẳng định đúng?
 0 b
 A. a b .B. a b . C. a b 10 . D. a 2b .
Câu 17. [2D3-2.1-1] Cho hai hàm số f x và g x liên tục trên đoạn a;b và số thực c thỏa mãn 
 a c b . Khẳng định nào sau đây sai?
 b b b
 A. f x g x dx f x dx g x dx .
 a a a
 b b
 B. kf x dx k f x dx ( k là hằng số khác 0).
 a a
 b b b
 C. f x g x dx f x dx. g x dx .
 a a a
 b c b
 D. f x dx f x dx f x dx .
 a a c
 3 2 3
Câu 18. [2D3-2.1-1] Cho hàm số y f x thỏa mãn f x dx 7 , f x dx 3. Tính f x dx .
 0 0 2
 A. 4 . B. 4. C. 5. D. 10.
 3 3
Câu 19. [2D3-2.1-1] Nếu f x dx 2 thì 3 f x 2 dx bằng
 1 1
 A. 6.B. 10.C. 8.D. 4.
Câu 20. [2D3-2.1-1] Cho hàm số y f x có đạo hàm liên tục trên đoạn 1;2 và thỏa mãn f 1 1, 
 2
 f 2 1. Giá trị của f x dx bằng
 1
 A. 2. B. 0. C. 2. D. 1.
 2 2
Câu 21. [2D3-2.1-2] Cho 3 f x 2x dx 5 . Tính I f x dx.
 1 1
 10 8 2
 A. . B. . C. . D. 1.
 3 3 3
Câu 22. [2D3-2.1-2] Cho hàm số y f (x) có đạo hàm liên tục trên 0;2 và thỏa mãn f (0) f (2) 1. 
 2
 Biết ex  f (x) f '(x)dx ae2 be c . Tính P a2021 b2021 c2021 .
 0
 A. 0. B. 1. C. 2. D. 3.
 3
Câu 23. [2D3-2.2-2] Cho hàm số y f x liên tục trên ¡ và f x dx 6 . Giá trị của 
 1
 2
 I cos x. f 2sin x 1 dx bằng: 
 0
 A. 3 . B. 12. C. 6 . D. 4 .
 2 2 x3
Câu 24. [2D3-2.2-2] Cho tích phân I dx , nếu đặt u x2 1 thì tích phân đã cho trở thành
 2
 0 x 1
 Trang 4 SP ĐỢT 15 TỔ 24 ĐỀ GIỮA KỲ 2 LỚP 12
 9 u 1 9 u 1 9 u 1 2 2 u 1
 A. I du . B. I du . C. I du . D. I du .
 1 2 u 1 2 u 1 2u 0 2 u
 2 ln x
Câu 25. [2D3-2.3-2] Cho I dx a b c ln 2 với a,b,c là các số nguyên dương. Tính 
 1 x
 P a b c
 A. P 44 . B. P 14. C. P 20 . D. P 6 .
Câu 26. [2H3-1.1-1] Trong không gian Oxyz , cho a 1; 2;0 , b 5;4; 1 . Tọa độ của vectơ 
 x 2a b bằng 
 A. 3;0; 1 . B. (7; 4;1) .C. (7; 8;1) .D. (7; 8; 1) .
Câu 27. [2H3-1.2-2] Trong không gian Oxyz , cho a 1; 3;2 , b 2,4;m . Định m để hai vectơ 
 a,b vuông góc với nhau.
 A. m 7 . B. m 7 . C. m 14 . D. m 2 .
Câu 28. [2H3-1.1-1] Trong không gian Oxyz , cho hai điểm A 1;2;1 ; B 3;0;3 . Tọa độ trung điểm I 
 của đoạn thẳng AB là 
 A. I 2;1;2 . B. I 1;2;1 . C. I 1; 1; 2 . D. I 1;1;2 .
Câu 29. [2H3-1.3-1] Trong không gian Oxyz , lập phương trình mặt cầu tâm I 1; 2;3 và có bán kính 
 R 5.
 A. x 1 2 y 2 2 z 3 2 25. B. x 1 2 y 2 2 z 3 2 25 .
 C. x 1 2 y 2 2 z 3 2 5 . D. x 1 2 y 2 2 z 3 2 5 .
Câu 30. [2H3-1.3-2] Trong không gian Oxyz , cho mặt cầu S có phương trình 
 x2 y2 z2 2y 4z 4 0 . Thể tích khối cầu S bằng
 A. 12 . B. 36 . C. 24 . D. 25 .
Câu 31. [2H3-2.3-1] Trong không gian Oxyz , cho hai điểm A 0;1;1 và B 1;2;3 . Viết phương trình 
 của mặt phẳng P đi qua A và vuông góc với đường thẳng AB .
 A. x y 2z 3 0 . B. x y 2z 6 0 .
 C. x 3y 4z 7 0 . D. x 3y 4z 26 0 .
Câu 32. [2H3-2.3-1] Trong không gian Oxyz , mặt phẳng nào dưới đây chứa trục Oy ?
 A. P : y 0 . B. Q : y 1. C. R : x z 0 . D. S : x z 1.
Câu 33. [2H3-2.3-1] Trong không gian Oxyz , cho ba điểm A 1;0;0 , B 0;2;0 ,C 0;0;3 . Mặt phẳng 
 nào dưới đây đi qua ba điểm A, B và C ?
 x y z
 A. R : x 2y 3z 1. B. Q : 1.
 1 2 3
 x y z
 C. S : x 2y 3z 1. D. P : 0 .
 1 2 3
Câu 34. [2H3-2.3-2] Trong không gian Oxyz , cho điểm M 2;0;1 . Gọi A , B lần lượt là hình chiếu 
 của M trên trục Ox và trên mặt phẳng Oyz . Viết phương trình mặt trung trực của đoạn AB .
 A. 4x 2z 3 0 . B. 4x 2y 3 0 . C. 4x 2z 3 0 . D. 4x 2z 3 0 .
 Trang 5 SP ĐỢT 15 TỔ 24 ĐỀ GIỮA KỲ 2 LỚP 12
Câu 35. [2H3-2.3-2] Trong không gian Oxyz , cho điểm M 4;2;3 .Viết phương trình mặt phẳng đi 
 qua ba điểm A, B,C lần lượt là hình chiếu của điểm M trên các trục Ox,Oy,Oz.
 A. 3x 6 y 4z 12 0 . B. 4x 2 y 3z 1 0 .
 C. 3x 6 y 4z 12 0 . D. 4x 2 y 3z 1 0 .
B. PHẦN TỰ LUẬN (3 ĐIỂM)
Câu 36. [2H2-1.1-3] Cho hình thang ABCD có ·ADC D· AB 90 , AB 7 (cm), CD 3 (cm), 
 AD 12 (cm). Gọi E là điểm trên cạnh BC sao cho BC 4BE . Tính thể tích khối tròn xoay 
 tạo thành khi cho miền tam giác ADE quay quanh trục AD .
 1
Câu 37. [2D3-2.1-4] Cho F x là một nguyên hàm của hàm số f x trên khoảng 1;1 và 
 x2 1
 thỏa mãn F 0 1. Tìm tất cả các nghiệm thuộc khoảng 1;1 của phương trình F x 2 . 
 e x ln2 x 3ln x 2
Câu 38. [2D3-2.3-3] Cho dx a.e b.ln e 1 c , với a,b,c là các số thực. Tính 
 1 1 x ln x
 giá trị biểu thức P a2 b2 c2 .
Câu 39. [2D3-2.3-4] Cho hàm số f x có đạo hàm liên tục trên đoạn 0;1 thỏa mãn f 1 3,
 1 1 1
 2 3
 f x dx 9 và x f x dx 1. Tính tích phân xf x dx .
 0 0 0
 --- HẾT ---
 Trang 6 SP ĐỢT 15 TỔ 24 ĐỀ GIỮA KỲ 2 LỚP 12
 BẢNG ĐÁP ÁN
 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20
 D B A A C C C B C A D D C A A B C B B A
 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35
 B A A B A C B D A B A C B A C
 HƯỚNG DẪN GIẢI
A. PHẦN TRẮC NGHIỆM (7 ĐIỂM)
Câu 1. [2D3-1.1-1] Khẳng định nào sau đây là khẳng định đúng? 
 3
 A. 3x2dx 6x C . B. 3x2dx 9x3 C . C. 3x2dx x C . D. 3x2dx x3 C .
 2 
 Lời giải
 FB tác giả: Nguyễn Thành Trung
 GV phản biện: Vạn Kiếm Sầu – Le Van Nhan
 Khẳng định đúng là 3x2dx x3 C .
Câu 2. [2D3-1.1-1] Hàm số y F x là một nguyên hàm của hàm số y f x . Hãy chọn khẳng 
 định đúng.
 A. F x f x .B. F x f x . C. F x f x C . D. F x C f x .
 Lời giải
 FB tác giả: Vạn Kiếm Sầu 
 GV phản biện: Nguyễn Hà – Vương Quang Minh
 Khẳng định đúng là: F x f x .
Câu 3. [2D3-1.1-1] Cho f x , g x là các hàm số xác định và liên tục trên ¡ . Trong các mệnh đề 
 sau, mệnh đề nào sai?
 A. f x g x dx f x dx. g x dx .
 B. 5 f x dx 5 f x dx .
 C. f x 3g x dx f x dx 3 g x dx .
 D. f x g x dx f x dx g x dx .
 Lời giải
 FB tác giả: Vương Quang Minh
 GV phản biện: Vạn Kiếm Sầu – Nguyễn Hà
 Khẳng định sai là: f x g x dx f x dx. g x dx .
Câu 4. [2D3-1.1-1] Trong các khẳng định sau, khẳng định nào sai?
 A. sin xdx cos x C . B. cos xdx sin x C . 
 C. 2xdx x2 C . D. exdx ex C .
 Lời giải
 FB tác giả: Nguyễn Hà
 GV phản biện: Vương Quang Minh, Trịnh Duy Phương
 Khẳng định sin xdx cos x C sai vì sin xdx cos x C .
 Trang 7 SP ĐỢT 15 TỔ 24 ĐỀ GIỮA KỲ 2 LỚP 12
Câu 5. [2D3-1.1-2] Tìm giá trị của m để hàm số F x m2 x3 3m 2 x2 4x 3 là một nguyên 
 hàm của hàm số f x 3x2 10x 4.
 A. m 1. B. m 2 . C. m 1. D. m 1.
 Lời giải
 FB tác giả: Trịnh Duy Phương
 GV phản biện: Qúy Nguyễn, Nguyễn Hà
 Ta có: F x 3m2 x2 2 3m 2 x 4 .
 Khi đó F x là một nguyên hàm của hàm số f x F x f x ,x ¡
 2
 3m 3 m 1
 m 1.
 2 3m 2 10 m 1
Câu 6. [2D3-1.1-2] Giả sử hàm số F x là một nguyên hàm của hàm số f x trên K . Khẳng định 
 nào sau đây đúng.
 A. Chỉ có duy nhất một hằng số C sao cho hàm số y F(x) C là một nguyên hàm của hàm 
 f trên K.
 B. Chỉ có duy nhất hàm số y F(x) là nguyên hàm của f trên K.
 C. Với mỗi nguyên hàm G của f trên K thì tồn tại một hằng số C sao cho G(x) F(x) C 
 với x thuộc K .
 D. Với mỗi nguyên hàm G của f trên K thì G(x) F(x) C với mọi x thuộc K và C bất 
 kỳ.
 Lời giải
 FB tác giả: Quý Nguyễn
 Phản biện: Trịnh Duy Phương, Bích Ngọc
 Dễ thấy với mỗi nguyên hàm G của f trên K thì tồn tại một hằng số C sao cho 
 G(x) F(x) C với x thuộc K .
Câu 7. [2D3-1.1-1] Mệnh đề nào sau đây sai ?
 A. Nếu f x dx F x C thì f t dt F t C .
 B. kf x dx k f x dx ( k là hằng số và k 0).
 C. f x dx f x C .
 D. f x f x dx f x dx f x dx .
 1 2 1 2 
 Lời giải
 FB tác giả: Bích Ngọc
 GV phản biện: Quý Nguyễn, Tuan Anh
 Mệnh đề C sai vì f x dx f x C .
Câu 8. [2D3-1.1-1] Cho hàm số f x xác định trên K . Chọn đẳng thức đúng? 
 A. f x dx f ' x C . B. f x g x dx f x dx g x dx .
 1
 C. kf x dx f x dx, k 0. D. f x .g x dx f x dx. g x dx .
 k 
 Lời giải
 FB tác giả: Tuấn Anh
 GV phản biện: Bích Ngọc – Ha Dang
 Trang 8 SP ĐỢT 15 TỔ 24 ĐỀ GIỮA KỲ 2 LỚP 12
 Dễ thấy f x g x dx f x dx g x dx là đẳng thức đúng theo tính chất.
 2021 1
Câu 9. [2D3-1.1-2] Tìm nguyên hàm của hàm số f x trên khoảng ;0 . 
 x x2
 1 1
 A. 2021.ln x C . B. 2021.ln x C .
 x x
 1 1
 C. 2021.ln x C . D. 2021.ln x C .
 x x
 Lời giải
 FB tác giả: Ha Dang
 GV phản biện: Tuan Anh – Nguyễn Duy Tân 
 Với x ;0 , ta có
 2021 1 1 1 1 1
 f x dx 2 dx 2021 dx 2 dx 2021.ln x C 2021.ln x C .
 x x x x x x
Câu 10. [2D3-1.1-2] Cho các hàm số y f (x) và y g(x) liên tục trên ¡ . Có bao nhiêu khẳng định 
 đúng trong các khẳng định sau?
 I. f (x)dx f (x) C .
 II. f (x)dx f (x) .
 III. k. f (x)dx k. f (x)dx (với k là hằng số).
 IV.  f (x) g(x)dx f (x)dx  g(x)dx .
 A. 0. B. 1. C. 2. D. 3.
 Lời giải
 FB tác giả: Nguyễn Duy Tân
 GV phản biện: Ha Dang, Đoàn Ánh Dương
 Giả sử f (x)dx F(x) C . Khi đó ta có:
 Khẳng định I sai vì f (x)dx F(x) C F (x) C f (x) .
 Khẳng định II sai vì f (x)dx f (x) C .
 Khẳng định III sai vì k. f (x)dx k. f (x)dx với điều kiện k 0 .
 Khẳng định IV sai vì  f (x) g(x)dx f (x)dx g(x)dx .
 Vậy không có khẳng định nào đúng trong các khẳng định trên.
Câu 11. [2D3-1.3-1] Hàm số f x x 2 ex có họ nguyên hàm là
 A. x 2 ex C .B. xex C .C. x 1 ex C . D. x 3 ex C .
 Lời giải
 FB tác giả: Đoàn Ánh Dương
 GV phản biện: Nguyen Duy Tân, Đoàn Nhật Thịnh
 Ta có: f x dx x 2 exdx .
 u x 2 du dx
 Đặt x x .
 dv e dx v e
 Do đó x 2 exdx x 2 ex exdx x 2 ex ex C x 3 ex C .
 Trang 9 SP ĐỢT 15 TỔ 24 ĐỀ GIỮA KỲ 2 LỚP 12
 Hoặc f x dx x 2 exdx x 2 d ex x 2 ex exdx x 3 ex C
Câu 12. [2D3-1.3-2] Cho hàm số f (x) (2x 1)e2x (x ¡ ) . Gọi F(x) là một nguyên hàm của f (x) 
 trên ¡ . Biết F(x) được viết dưới dạng F(x) (a.x b).em.x C , (a, b, m ¥ ) . Tính 
 T a b m .
 A. 12. B. 7. C. 4.D. 3.
 Lời giải
 FB tác giả: Đoàn Nhật Thịnh
 GV phản biện: Đoàn Ánh Dương – Ngát Nguyễn
 Ta có F(x) f (x)dx (2x 1)e2xdx .
 du 2.dx
 u 2x 1 
 Đặt 2x 1 2x .
 dv e dx v e
 2
 Theo công thức nguyên hàm từng phần ta có:
 1 1 1
 F(x) (2x 1)e2x e2xdx (2x 1)e2x e2x C x.e2x C .
 2 2 2
 Vậy F(x) x.e2x C a 1, b 0, m 2. Do đó ta có T 3.
Câu 13. [2D3-2.1-1] Cho hàm số f x liên tục trên 0;1 và f 1 f 0 2 . Tính tích phân 
 1
 I f x dx .
 0
 A. I 1. B. I 1. C. I 2 . D. I 0 .
 Lời giải
 FB tác giả: Ngát Nguyễn
 GV phản biện: Đoàn Nhật Thịnh – Ngân Bùi 
 1
 1
 Ta có: I f x dx f x f 1 f 0 2 .
 0 
 0
 2020
Câu 14. [2D3-2.1-1] Tính tích phân I 7xdx . 
 0
 72020 1 72021
 A. I .B. I 72020 ln 7 .C. I 7 . D. I 2020.72019 .
 ln 7 2021
 Lời giải
 Tác giả: Ngân Bùi
 Phản biện: Ngát Nguyễn – Nguyễn Tri Đức
 Theo định nghĩa tích phân ta có: 
 2020 x 2020 0 2020
 x 7 2020 7 7 7 1
 I 7 dx 
 0 ln 7 0 ln 7 ln 7 ln 7
Câu 15. [2D3-1.1-1] Tìm nguyên hàm F x 2dx . 
 3 2 x2
 A. F x 2 x C . B. F x 2 x C . C. F x C . D. F x C .
 3 2
 Lời giải
 FB tác giả: Nguyễn Tri Đức
 GV phản biện: Ngát Nguyễn – Lê Minh Tâm
 Trang 10