Đề cương ôn tập môn Hình học Lớp 8 - Bài 6: Trường hợp đồng dạng thứ hai

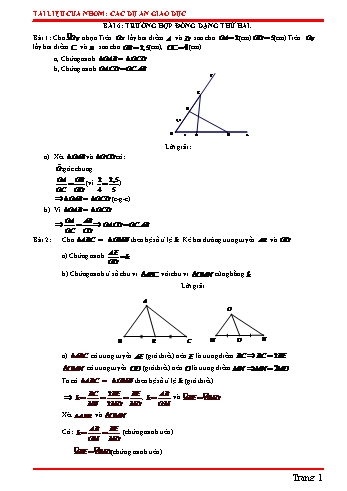
 TÀI LIỆU CỦA NHÓM: CÁC DỰ ÁN GIÁO DỤC
 BÀI 6: TRƯỜNG HỢP ĐỒNG DẠNG THỨ HAI.
Bài 1: Cho x· Oy nhọn. Trên Ox lấy hai điểm A và D sao cho OA 2 (cm)OD 5(cm).Trên Oy 
lấy hai điểm C và B sao cho OB 2,5(cm), OC 4 (cm)
 a, Chứng minh OAB ∽ OCD .
 b, Chứng minh OA.CD OC.AB .
 y
 C
 B
 2,5
 O 2 A D x
 Lời giải:
 a) Xét OAB và OCD có:
 Oˆ :góc chung
 OA OB 2 2,5
 (vì )
 OC OD 4 5
 OAB ∽ OCD (c-g-c)
 b) Vì OAB ∽ OCD
 OA AB
 OA.CD OC.AB
 OC CD
Bài 2: Cho ABC ∽ OMN theo hệ số tỉ lệ k . Kẻ hai đường trung tuyến AE và OD .
 AE
 a) Chứng minh k .
 OD
 b) Chứng minh tỉ số chu vi ABC với chu vi OMN cũng bằng k .
 Lời giải
 A
 O
 B E C M D N
 a) ABC có trung tuyến AE (giả thiết) nên E là trung điểm BC BC 2BE
 OMN có trung tuyến OD (giả thiết) nên O là trung điểm MN MN 2MD
 Ta có ABC ∽ OMN theo hệ số tỉ lệ k (giả thiết)
 BC 2BE BE AB
 k ; k và ·ABE O· MD .
 MN 2MD MD OM
 Xét ABE và OMN
 AB BE
 Có: k (chứng minh trên)
 OM MD
 ·ABE O· MD (chứng minh trên)
 Trang 1 TÀI LIỆU CỦA NHÓM: CÁC DỰ ÁN GIÁO DỤC
 ABE ∽ OMD theo hệ số tỉ lệ k (c-g-c)
 AE
 k
 OD
 b) Chứng minh tỉ số chu vi ABC với chu vi OMN cũng bằng k .
 Ta có ABC ∽ OMN theo hệ số tỉ lệ k (giả thiết)
 AB AC BC
 k 
 OM ON MN
 Áp dung tính chất dãy tỉ số bằng nhau ta được:
 AB AC BC AB AC BC C
 k ABC
 OM ON MN OM ON MN C OMN
Bài 3: Cho ABC cân tại A . Gọi M là trung điểm của BC . Lấy K thuộc cạnh AB và I thuộc 
 cạnh AC sao cho K· MI ·ABC .
 a) Chứng minh BMK ∽ CIM .
 b) Chứng minh CMI ∽ MIK .
 Lời giải
 A
 K
 I
 B M C
 a) Chứng minh BMK ∽ CIM .
 Có: K· MI ·ABC (giả thiết) và ·ABC ·ACB (do ABC cân tại A ) 
 K· MI M· CI 1 
 Có: B· MK K· MI I·MC 180(do ba điểm B,M ,C thẳng hàng)
 B· MK 180 K· MI I·MC 2 
 Trong CIM có: M· IC I·MC M· CI 1800 (định lí tổng ba góc trong tam giác)
 M· IC 180 M· CI I·MC 3 
 Từ 1 , 2 & 3 B· MK M· IC
 Xét BMK và CIM có:
 B· MK M· IC (chứng minh trên) 
 K· BM M· CI (do ABC cân tại A ) 
 BMK ∽ CIM (g-g).
 Trang 2 TÀI LIỆU CỦA NHÓM: CÁC DỰ ÁN GIÁO DỤC
 b) Chứng minh CMI ∽ MIK .
 Ta có BMK ∽ CIM (chứng minh trên) 
 BM MK CM MK
 (do M là trung điểm của BC )
 CI IM CI IM
 Xét CMI và MIK có: 
 CM MK
 (chứng minh trên) 
 CI IM
 K· MI M· CI (chứng minh trên) 
 CMI ∽ MIK (c-g-c)
Bài 4: Cho hình thoi ABCD có µA 600 . Đường thẳng qua C cắt tia đối của tia BA , DA ở M và N .
 a) Chứng minh BCM ∽ DNC rồi viết tỉ số đồng dạng.
 b) Chứng minh BM.DN BD2 .
 Lời giải
 M
 B
 A C
 D
 N
 a) Chứng minh BCM ∽ DNC
 -Ta có ABCD là hình thoi (giả thiết) 
 CD//AB , BC//AD hay CD//AM , BC//AN
 N· CD C· MB , C· ND M· CB (các cặp góc ở vị trí đồng vị)
 Xét CMI và MIK có: 
 N· CD C· MB (chứng minh trên)
 C· ND M· CB (chứng minh trên)
 BCM ∽ DNC (g-g)
 -Viết tỉ số đồng dạng: 
 Có: BCM ∽ DNC (chứng minh trên)
 BC BM CM
 DN DC NC
 b) Chứng minh BM.DN BD2 .
 BC BM
 Có: (chứng minh trên)
 DN DC
 BM.DN BC.DC 1 
 Trang 3 TÀI LIỆU CỦA NHÓM: CÁC DỰ ÁN GIÁO DỤC
 Do ABCD là hình thoi có µA 600 (giả thiết)
 BCD đều BC DC BD 2 
 Từ 1 & 2 BM.DN BD2
Bài 5: Cho ABC cân tại A , H là trung điểm của BC . Gọi I là hình chiếu của H trên AC và O là 
 trung điểm của HI . Chứng minh:
 a) ·AHO B· CI .
 b) Chứng minh AH.IC HI.HC HO.BC .
 c) AHO ∽ BCI .
 d) Chứng minh AO  BI .
 Lời giải
 A
 I
 O
 B H C
 a) ·AHO B· CI .
 Có ABC cân tại A , H là trung điểm của BC (giả thiết)
 Đường trung tuyến AH đồng thời là đường cao của ABC
 Hay AH  BC
 Có I là hình chiếu của H trên AC (giả thiết) HI  AC
 ·AHI H· CI (cùng phụ với I·HC ) hay ·AHO B· CI .
 b) Chứng minh AH.IC HI.HC HO.BC .
 - Xét AIH và HIC có 
 ·AHI H· CI (chứng minh trên) 
 ·AIH H· IC 90
 AIH ∽ HIC (g-g)
 AH IH
 AH.IC HI.HC 1 
 HC IC
 1 
 Ta có HI.HC 2HO BC HO.BC 2 
 2 
 Từ 1 & 2 AH.IC HI.HC HO.BC
 c) Chứng minh AHO ∽ BCI .
 Trang 4 TÀI LIỆU CỦA NHÓM: CÁC DỰ ÁN GIÁO DỤC
 AH BC
 Có AH.IC HO.BC (chứng minh trên) 
 HO IC
 - Xét AHO và BCI 
 Có: ·AHI H· CI (chứng minh trên) 
 AH BC
 (chứng minh trên) 
 HO IC
 AHO ∽ BCI (c-g-c).
 d) Chứng minh AO  BI .
 Có AHO ” BCI (chứng minh trên) H· AO C· BI
 Có AH  BC (chứng minh trên) ·ABH B· AH 90 
 C· BI I·BA B· AH 90 
 H· AO I·BA B· AH 90 ( do H· AO C· BI )
 O· AB I·BA 90 
 AO  BI 
Bài 6: Cho ABC cân tại A có AB AC 5cm, BC 6cm . Tia phân giác Bµ cắt AC tại M , phân 
 giác góc Cµ cắt AB tại N .
 a) Chứng minh ANC ∽ AMB .
 b) Chứng minh MN //BC và độ dài cạnh AM .
 c) Tính diện tích AMN . Biết diện tích ABC là 12cm2
 Lời giải
 A
 N M
 B C
 a) Chứng minh ANC ∽ AMB .
 ABC cân tại A
 Có tia phân giác Bµ cắt AC tại M , phân giác góc Cµ cắt AB tại N (giả thiết)
 nên ·ABM ·ACN .
 - Xét ANC và AMB có: 
 ·ABC (chứng minh trên) 
 ·ABM ·ACN (chứng minh trên) 
 ANC ∽ AMB (g-g).
 Trang 5 TÀI LIỆU CỦA NHÓM: CÁC DỰ ÁN GIÁO DỤC
 b) Chứng minh MN //BC và độ dài cạnh AM .
 Do ANC ∽ AMB (chứng minh trên) 
 AN AC
 AM AB
 AN AM
 (do AB AC )
 AB AC
 MN //BC (định lý Talet đảo).
 Áp dụng tính chất đường phân giác của tam giác và tính chất của dãy tỉ số bằng nhau, ta có:
 AM MC AM MC AC 5 5 AM 5 25
 AM cm 
 AB BC AB BC AB BC 5 6 11 5 11 11
 c) Tính diện tích AMN . Biết diện tích ABC là 12cm2 .
 Do: MN //BC (chứng minh trên) nên AMN ∽ ABC ( định lí) 
 25
 AM 5
 Theo hệ số: 11 
 AC 5 11
 2 2
 S AMN AM S AMN 5 S AMN 25 12.25 300 2
 S AMN cm 
 S ABC AC 12 11 12 121 121 121
Bài 7: 
 Cho hình thang vuông ABCD có AB//CD và µA Dµ 900 . Biết CD 2AB 2AD .
 a) BCD là tam giác gì? Vì sao?
 b) Chứng minh ABD ∽ BCD .
 c) Kẻ đường cao BH . Chứng minh AB.BC BD.HC . 
 Lời giải
 A B
 D H C
 a) Kẻ BH  CD H CD 
 Tứ giác ABHD có µA ·ADH B· HD 90
 Nên tứ giác ABHD là hình chữ nhật
 1 
 Mà AB AD CD 
 2 
 Nên tứ giác ABHD là hình vuông
 BH HD AD
 1 1
 Mà AD CD BH DH CD
 2 2
 HD HC H là trung điểm của CD
 BDC có BH là đường trung tuyến
 Trang 6 TÀI LIỆU CỦA NHÓM: CÁC DỰ ÁN GIÁO DỤC
 1
 Mà BH CD
 2
 BCD vuông tại B 1 
 B· DC B· CD 90
 Vì ABCD là hình vuông nên DB là phân giác của ·ADH
 Mà ·ADH 90
 B· DC 45
 Mà B· DC B· CD 90 B· CD 45
 B· DC B· CD
 BDC cân tại B 2 
 Từ 1 và 2 BDC vuông cân tại B .
 b) Xét ABD và BCD có: 
 B· AD C· BD 90 
 ·ABD B· DC (hai góc so le trong do AB // CD )
 ABD ∽ BDC (g-g)
 c) Xét ABD và HCB có: 
 B· AD B· HC 90 
 ·ABD B· CH 45 
 ABD ∽ HCB (g-g)
 AB BD
 HC BC
 AB.BC BD.HC
Bài 8: 
 Cho hình thang ABCD , AB//CD có Aˆ Dˆ 90, AB 4 (cm), CD 9 (cm), BC 13
 (cm). M là trung điểm của AD . Kẻ BK  CD tại K .
 a) Tứ giác ABKD là hình gì? Tính KC, BK, AD và AM .
 b) Chứng minh ABM ∽ DMC .
 c) Tính B· MC .
 Lời giải
 A B
 M
 D C
 K
 a) Tứ giác ABKD có µA ·ADK B· KD 90
 Nên tứ giác ABKD là hình chữ nhật
 AD BK; AB DK
 Trang 7 TÀI LIỆU CỦA NHÓM: CÁC DỰ ÁN GIÁO DỤC
 Mà AB 4 (cm) nên DK 4 (cm)
 Có DK KC DC KC DC DK KC 9 4 KC 5 (cm) 
 BKC vuông tại K nên BC 2 BK 2 KC 2
 BK 2 BC 2 KC 2
 BK 2 169 25 144
 BK 12 (cm) 
 Mà AD BK
 AD 12 (cm)
 1
 Có MD AM AD (vì là trung điểm của AD )
 2
 AM 6 (cm) , DM 6 (cm)
 b) 
 AM 2
 Có AM 6 (cm), DC 9 (cm) 
 DC 3
 AB 2
 Có AB 4 (cm), DM 6 (cm), 
 DM 3
 AM AB
 DC DM
 Xét ABM và DMC có 
 B· AM M· DC 90 
 AM AB
 DC DM
 ABM ∽ DMC c g c .
 c) Tính B· MC .
 Có ABM ∽ DMC
 ·AMB D· CM
 DCM vuông tại D nên D· CM D· MC 90
 ·AMB D· MC 90
 Có ·AMB D· MC B· MC 180
 B· MC 90
Bài 9: 
 Cho DEF có DE 6 (cm), DF 12 (cm). Trên cạnh DF lấy điểm B sao cho BD 3 (cm). 
 a) Chứng minh EBD ∽ FDE .
 b) Kẻ phân giác trong DA của DEF . Chứng minh AE.DE AF.BD .
 c) Gọi P,Q lần lượt là trung điểm của BE và FE . Gọi H là giao điểm PQ với DA . 
 HP.DF
 Chứng minh 1.
 HQ.DE
 E
 A
 P Q
 H
 F
 D B
 Trang 8 TÀI LIỆU CỦA NHÓM: CÁC DỰ ÁN GIÁO DỤC
 Lời giải
 DE 1
 a) Có DE 6 (cm), DF 12 (cm) 
 DF 2
 DE BD
 DF DE
 Xét EBD và FDE có:
 E· DF : góc chung
 DE BD
 DF DE
 EBD ∽ FED c g c .
 b) Có EBD ∽ FED
 BD ED
 (định nghĩa hai tam giác đồng dạng)
 ED FD
 Xét EDF có DA là phân giác 
 AE ED AE BD
 AF FD AF ED
 AE.DE AF.BD .
 HP.DF
 c) 1
 HQ.DE
 AE ED 1 EA 1
 Có 
 AF FD 2 EF 3
 EQ 1
 Có ( vì Q là trung điểm của FE ) 
 EF 2
 AE 2 AQ 1
 EQ 3 EQ 3
 AQ 1
 (vì QE QF )
 QF 3
 DB 1 AQ DB
 mà . 
 BF 3 QF BF
 AQ DB
 Xét FAD có 
 QF BF
 BQ// AD (định lí Ta-let đảo) .
 Xét EBF có P,Q lần lượt là trung điểm của BE và FE
 1
 PQ là đường trung bình của EBF PQ BF 1 
 2
 HQ AQ 1 AQ 1
 Xét ADF có HQ//DF nên (vì )
 DF AF 4 QF 3
 Tứ giác DHQB có HQ//DB , DH //BQ
 Tứ giác DHQB là hình bình hành 
 HQ DB
 DB 1 DB 1
 DF 4 BF 3
 Trang 9 TÀI LIỆU CỦA NHÓM: CÁC DỰ ÁN GIÁO DỤC
 HQ 1
 BF 3HQ 2 
 BF 3
 3 1
 Từ 1 và 2 PQ HQ PH HQ
 2 2
 PH 1
 QH 2
 DF HP.DF
 Mà 2 1
 DE HQ.DE
Bài 10: Cho ABC vuông tại A. M là trung điểm của AC , Từ M vẽ đường thẳng d vuông góc với
 1
 AC . Trên d lấy điểm N sao cho MN AB và N và B nằm trên hai nửa mặt phẳng bờ
 2
 AC .
 a) Chứng minh ABC ∽ MNC .
 b) AB cắt CN tại D , Chứng minh CMN ∽ CAD .
 c) Chứng minh BC DC .
 Lời giải
 B
 A C
 M
 N
 D
 AC
 a) Có M là trung điểm của AC nên 2
 MC
 1 AB
 Có MN AB nên 2
 2 MN
 AB AC
 MN MC
 Xét ABC và MNC có:
 B· AC C· MN 90 
 AB AC
 MN MC
 ABC ∽ MNC c g c .
 b) Xét CAD có M là trung điểm của AC
 MN // AD (vì cùng  AC )
 N là trung điểm của CD
 Xét CAD có M là trung điểm của AC
 N là trung điểm của CD
 MN là đường trung bình của CAD
 1 MN 1
 MN AD 
 2 AD 2
 1
 Mà CM CA
 2
 Trang 10