Đề cương ôn tập môn Hình học Lớp 8 - Bài 1: Định lí ta lét trong tam giác

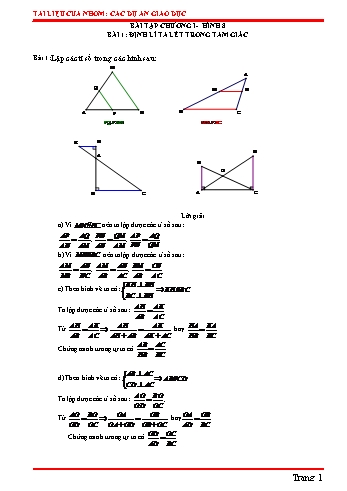
 TÀI LIỆU CỦA NHÓM: CÁC DỰ ÁN GIÁO DỤC
 BÀI TẬP CHƯƠNG I- HÌNH 8
 BÀI 1: ĐỊNH LÍ TA LÉT TRONG TAM GIÁC
Bài 1:Lập các tỉ số trong các hình sau:
 M
 A
 Q M N
 A P N B C
 PQ // MN MN // BC
 K H
 D
 A
 B
 O
 B C A C
 Lời giải
 a) Vì MN //BC nên ta lập được các tỉ số sau: 
 AP AQ PN QM AP AQ
 ; ; 
 AN AM AN AM PN QM
 b) Vì MN //BC nên ta lập được các tỉ số sau: 
 AM AN AM AN BM CN
 ; ; 
 MB NC AB AC AB AC
 KH  BH
 c) Theo hình vẽ ta có: KH //BC
 BC  BH
 AH AK
 Ta lập được các tỉ số sau: 
 AB AC
 AH AK AH AK HA KA
 Từ hay 
 AB AC AH AB AK AC HB KC
 AB AC
 Chứng minh tương tự ta có 
 HB KC
 AB  AC
 d) Theo hình vẽ ta có: AB//CD
 CD  AC
 AO BO
 Ta lập được các tỉ số sau: ; 
 OD OC
 AO BO OA OB OA OB
 Từ hay 
 OD OC OA OD OB OC AD BC
 OD OC
 Chứng minh tương tự ta có 
 AD BC
 Trang 1 TÀI LIỆU CỦA NHÓM: CÁC DỰ ÁN GIÁO DỤC
Bài 2: Tìm x trong các hình sau đây:
 A
 x 3
 N M
 4
 3
 B C
 MN // BC
 N 
 B 8
 x
 O
 3 4,2
 A M
 AB // MN
 Lời giải
 AN AM x 3 3.3
 a) Ta có MN //BC nên hay x 2,25
 NB MC 3 4 4
 AB  BC
 b) Theo hình vẽ, ta có AB//FE
 FE  BC
 EC CF 2 2,5 4.2,5
 Suy ra ( định lí Ta lét) hay x 5
 CB CA 2 2 x 2
 OA OB 3 x 3.4,2
 c) Vì AB//MN nên hay x 1,575
 ON OM 8 4,2 8
 BH BK x 4 7.4
 d) Ta có HK //AI , theo định lí Ta lét hay x 3,5
 BA BI 7 4 4 8
Bài 3: Cho ABC có AB 4cm . Lấy D trên AB sao cho AD 3cm . Từ D kẻ đường thẳng song song 
với BC cắt AC tại E . Giả sử AE AC 14cm . 
 AE A
 a) Tính tỉ số .
 AC
 b) Tính AE; AC và EC
 D E
 B C
 Lời giải
 AE AD 3
 a) Theo giả thiết DE//BC nên ( định lí Ta- lét). 
 AC AB 4
 AE 3
 b) Theo câu a ta có 
 AC 4
 Theo giả thiết AE AC 14
 Trang 2 TÀI LIỆU CỦA NHÓM: CÁC DỰ ÁN GIÁO DỤC
 AE 3 AE 3 AE 3
 Do đó: hay 
 AC 4 AE AC 3 4 14 7
 14.3
 AE 6 (cm)
 7
 AC 14 6 8 (cm)
 Suy ra EC AC AE 8 6 2 (cm)
Bài 4: Cho x· Ay 900 . Trên tia Ax lấy hai điểm B và C sao cho AB 3cm, BC 2cm ( B nằm 
 giữa A và C ). Trên tia Ay lấy điểm E sao cho AE 2,5cm . Từ C kẻ đường thẳng song 
 y
 song với BE cắt Ay tại F . Tính độ dài đoạn EF .
 F
 E
 2,5
 x
 A 3 B 2 C
 Lời giải
 AE AB
 Theo giả thiết BE//CF nên ta có ( định lí Ta lét)
 EF BC
 2,5 3 2.2,5 5
 Hay suy ra EF (cm)
 EF 2 3 3
 5
 Vậy EF cm.
 3
Bài 5: Cho OBC có OB 2cm,OC 3cm . Trên tia đối của tia OB lấy điểm A sao cho OA 2,5cm . 
Đường thẳng đi qua A và song song với BC cắt OC tại D . TínhOD . D A
Lời giải 2,5
 OD OA O
 Theo giả thiết AD//BC nên ( định lí Ta lét)
 OC OB 2 3
 OD 2,5 3.2,5
 Hay OD 3,75 ( cm)
 3 2 2 B C
 Vậy OD 3,75 cm.
Bài 6: Cho ABC có trung tuyến BM và trọng tâm G . Qua G kẻ đường thẳng song song với AC cắt 
BA và BC lần lượt tại D và E . Giả sử chu vi ABC là 75 và AD EC 16 .
 a, Chứng minh BD 2.AD và BE 2.CE .
 b, Tính BA BC và tính AC, DE .
 A
 I
 D M
 G
 C
 B E
 Trang 3 TÀI LIỆU CỦA NHÓM: CÁC DỰ ÁN GIÁO DỤC
Lời giải
 a, Ta có BM là trung tuyến, G là trọng tâm của ABC nên BG 2.GM
 BD BG 2.GM
 Áp dụng định lí Talet: DG // AM (gt) 2 BD 2.DA
 DA GM GM
 BE BG 2.GM
 EG // CM (gt) 2 BE 2.EC
 EC GM GM
 b, 
 *) Tính BA BC 
 BA
 Theo câu a, ta có BD 2.DA BA 3.DA 3
 DA
 Do DE // AC , áp dụng định lí Talét và tính chất dãy tỉ số bằng nhau ta có:
 BA BC BA BC BA BC
 3 BA BC 16.3 48
 DA EC DA EC 16
 *) Tính AC, DE .
 Chu vi của ABC là 75 nên ta có: AC BA BC 75 AC 75 BA BC 75 48 27
 Dựng DI //BC I AC , khi đó tứ giác DICE là hình bình hành, nên DE IC .
 AC AB 3 AI IC IC IC
 Do DI //BC , áp dụng định lí Talet ta có: 3 1 3 2
 AI AD 1 AI AI AI
 IC 2 2 2
 Khi đó IC .AC .27 18cm hay DE 18cm
 AC 3 3 3
Bài 7: Cho hình thang ABCD có AB // CD. Lấy điểm I trên cạnh AD . Từ I kẻ đường thẳng song 
song với AB cắt BC tại K . AC cắt IK tại O . Chứng minh:
 AI AO
 a, .
 AD AC
 BK AO
 b, rồi suy ra AI.BC AD.BK .
 BC AC
 Lời giải
 A B
 O
 I K
 D C
 a, Do IK // AB , mà AB // CD nên IK // CD , do đó OI // CD
 AI AO
 Áp dụng định lí Talet ta có: 
 AD AC
 BK AO
 b, Do OK // AB nên áp dụng Định lí Talet ta có .
 BC AC
 AI AO AI BK
 Theo câu a, ta có AI.BC AD.BK
 AD AC AD BC
 Trang 4 TÀI LIỆU CỦA NHÓM: CÁC DỰ ÁN GIÁO DỤC
Bài 8: Cho ABC vuông tại A có AB 6cm, AC 8cm . Đường trung tuyến AM . Trên tia đối của tia 
 2
MA lấy điểm H sao cho MH .AM . Từ H kẻ đường thẳng vuông góc với AC cắt BC tại G .
 5
 a, Tính MG .
 b, Từ H kẻ đường thẳng song song với BC cắt AB và AC lần lượt tại I và K . Tính AI và 
 AK .
 Lời giải
 I
 B
 H
 M
 G
 A C K
 Áp dụng định lí Pitago cho tam giác vuông ABC ta có:
 BC 2 AB2 AC 2 62 82 100 BC 10cm
 BC 10
 M là trung điểm của BC , nên MB MC 5cm
 2 2
 Do AB // HG  AC , áp dụng định lí Talet ta có: 
 MG MH 2 2 2
 MG .MB .5 2cm
 MB MA 5 5 5
 2 MH AM MH AM AH 7
 b, Theo đề bài MH .AM AH .AM
 5 2 5 2 5 7 5
 Áp dụng định lí Talet:
 AI AH 7 7 7
 BM // IH (gt) AI .AB .6 8,4cm
 AB AM 5 5 5
 AK AH 7 7 7
 MC // HK (gt) AK .AC .8 11,2 cm
 AC AM 5 5 5
 BD 2
Bài 9: Cho ABC , Điểm D thuộc cạnh BC sao cho , Điểm E thuộc đoạn AD sao cho 
 DC 3
 AI
AE 2.DE . Gọi I là giao điểm BE và AC . Kẻ DN //BI . Tính tỉ số .
 IC
 Lời giải
 A
 I
 E N
 B D C
 Trang 5 TÀI LIỆU CỦA NHÓM: CÁC DỰ ÁN GIÁO DỤC
 Áp dụng định lí Talet do có:
 AI AE
 EI // DN 2 AI 2.IN (1)
 IN ED
 IC BC 5 5
 ND // IB IC .IN (2) 
 IN BD 2 2
 IA 4
 Từ (1) và (2) suy ra 
 IC 5
Bài 10: Cho ABC vuông tại B có AB 3cm, BC 4cm . Trung tuyến AM và trọng tâm G . Đường 
thẳng đi qua G và song song với BC cắt AB và AC lần lượt tại E và F .
 a, Tính AE và AF .
 BG
 b, Tính BG và lập tỉ số .
 AC
 Lời giải
 A
 I
 G
 E F
 C
 B M
 a, Áp dụng định lí Pitago cho tam giác vuông ABC ta có:
 AC 2 AB2 BC 2 32 42 25 AC 5 cm
 Do EG // BM và GF // MC nên áp dụng định lí Talet ta có:
 AE AG 2 2 2
 AE .AB .3 2 cm
 AB AM 3 3 3
 AF AG 2 2 2 10
 AF .AC .5 cm
 AC AM 3 3 3 3
 2
 b, Do G là trọng tâm của tam giác ABC nên BG .BI , 
 3
 1
 mà BI .AC (Tính chất đường trung tuyến ứng với cạnh huyền), 
 2
 2 1 1 BG 1
 suy ra BG . .AC .AC 
 3 2 3 AC 3
Bài 11: Cho hình bình hành ABCD . Vẽ tia Ax cắt đường chéo BD tại I , cắt BC tại J và cắt CD tại 
K .
 ID
 a) Tìm các tỉ số bằng với tỉ số và chứng minh IA2 = IJ.IK .
 IB
 Trang 6 TÀI LIỆU CỦA NHÓM: CÁC DỰ ÁN GIÁO DỤC
 AI
 b) Tìm các tỉ số bằng với tỉ số .
 AJ
 Lời giải
 ID
 a) Tìm các tỉ số bằng với tỉ số và chứng minh IA2 = IJ.IK .
 IB
 Tứ giác ABCD là hình bình hành nên AB // CD; AD // BC
 Áp dụng định lí Talet ta có: A B
 AID có AD // BJ AD // BC 
 ID IA
 1 I
 IB IJ
 AIB có AB // DK AB // CD D K C
 ID IK J
 2 
 IB IA
 ID IA IK
 Từ 1 và 2 
 IB IJ IA
 IA IK
 Vì IA2 = IJ.IK . 
 IJ IA
 AI
 b) Tìm các tỉ số bằng với tỉ số .
 AJ
 AI DI
 AID có AD // BJ . Áp dụng định lý Talet ta có: =
 AJ DB
 AI IK IA IK AI IK
 Từ 
 IJ IA IJ IA IK IA AJ AK
 AI DI KI
 Vậy = = .
 AJ DB AK
 Bài 12: Cho ABC . Lấy điểm D tùy ý trên BC . Kẻ tia Bx // AD và Bx cắt AC ở I . Kẻ tia 
 1 1 1
 Cy // AD và Cy cắt AB ở K . Chứng minh + = .
 BI CK AD
 Lời giải
 y
 K
 x
 I
 A
 M N
 C
 B D
 Qua A kẻ đường thẳng song song với BC cắt Bx tại M cắt Cy tại N
 Xét tứ giác BDAM có: BD // AM ; BM // AD
 Tứ giác BDAM là hình bình hành , suy ra BD =AM ; BM AD
 Chứng minh tương tự ta có tứ giác ADCN là hình bình hành , suy ra CD =AN; CN AD
 Trang 7 TÀI LIỆU CỦA NHÓM: CÁC DỰ ÁN GIÁO DỤC
 MB AC
 BCI có AM // BC (Định lý Talet) 1 
 IB IC
 DC AC
 BCI có AD // BI (Định lý Talet) 2 
 BC IC
 Mà MB AD (cmt) 3 
 DC AD
 Từ 1 , 2 và 3 4 
 BC IB
 AB BD
 BCK có: AD // CK (Định lý Talet) 
 BK BC
 AB NC AD
 AN // BC AD NC 
 BK CK CK
 AD BD
 Do đó 5 
 CK BC
 AD AD DC BD DC BD BC
 Từ 4 và 5 ta có 1
 IB CK BC BC BC BC
 1 1 
 AD 1
 BI CK 
 1 1 1
 + = .
 BI CK AD
Bài 13: Cho ABC có AD là đường trung tuyến. Trọng tậm là điểm G , một đường thẳng đi qua G 
 cắt các cạnh AB , AC lần lượt tại các điểm E và F . Từ B và C kẻ các đường thẳng song 
 BE CF
 song với EF cắt AD lần lượt tại M và N . Chứng minh rằng 1.
 AE AF
 Lời giải
 Ta có: BM // EF ; CN // EF BM // CN
 Xét BDM và CDN có 
 DB DC ( AD là đường trung tuyến)
 B· DM C· DN (hai góc đối đỉnh)
 D· BM D· CN (hai góc so le trong; BM // CN )
 BDM CDN (g.c.g)
 MD DN A
 BE GM
 Vì BM // EF (Định lý Talet)
 AE AG
 CF GN
 Vì CN // EF (Định lý Talet) F
 AF AG G
 BE CF GM GN GM GN M
 E
 AE AF AG AG AG
 B D C
 GD MD DN GD 2GD AG
 1 N
 AG AG AG
 BE CF
 Vậy 1.
 AE AF
 Trang 8 TÀI LIỆU CỦA NHÓM: CÁC DỰ ÁN GIÁO DỤC
Bài 14: Cho ABC có trung tuyến AO . vàG là trọng tâm, một đường thẳng bất kì đi qua G cắt các 
 cạnh AB , AC lần lượt tại các điểm M và N . Từ B và C kẻ các đường thẳng song song 
 AB AC
 với MN cắt AO lần lượt tại H và K . Chứng minh rằng + = 3.
 AM AN
 Lời giải
 Ta có: BH // MN ; CK // MN BH // CK H· BO O· CK (hai góc so le trong)
 Xét BHO và CKO có :
 A
 OB OC ( AO là trung tuyến của ABC )
 B· OH C· OK (hai góc đối đỉnh)
 · ·
 HBO OCK (cmt) N
 BHO CKO (g.c.g) G
 M
 OH OK H
 AB AH C
 Vì BH // MG 1 B O
 AM AG K
 AC AK
 Vì CK // GN 2 
 AN AG
 Cộng 1 và 2 theo vế ta được:
 AB AC AH AK AG GH AG GH HK 2AG 2GO 2AO
 AM AN AG AG AG AG AG
 Mà ABC có trung tuyến AO và G là trọng tâm
 2AO
 AG 2AO 3AG
 3
 AB AC 2AO 3AG
 Nên 3
 AM AN AG AG
 AB AC
 Vậy + = 3
 AM AN
 Trang 9