Đề thi tốt nghiệp THPT môn Toán Lớp 12 - Năm học 2020-2021 (Có đáp án)

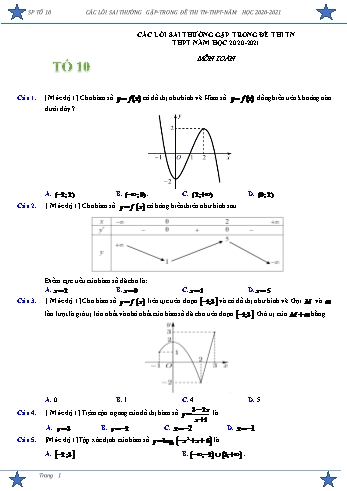
 SP TỔ 10 CÁC LỖI SAI THƯỜNG GẶP-TRONG ĐỀ THI TN-THPT-NĂM HỌC 2020-2021
 CÁC LỖI SAI THƯỜNG GẶP TRONG ĐỀ THI TN 
 THPT NĂM HỌC 2020-2021
 MÔN TOÁN
 TỔ 10
Câu 1. [ Mức độ 1] Cho hàm số y f (x) có đồ thị như hình vẽ. Hàm số y f (x) đồng biến trên khoảng nào 
 dưới đây ?
 A. ( 2;2) . B. ( ;0) . C. (2; ) . D. (0;2) .
Câu 2. [ Mức độ 1] Cho hàm số y f x có bảng biến thiên như hình sau
 Điểm cực tiểu của hàm số đã cho là:
 A. x 2 .B. x 0 . C. x 1. D. x 5.
Câu 3. [ Mức độ 1] Cho hàm số y f x liên tục trên đoạn  1;3 và có đồ thị như hình vẽ. Gọi M và m 
 lần lượt là giá trị lớn nhất và nhỏ nhất của hàm số đã cho trên đoạn  1;3 . Giá trị của M m bằng
 A. 0. B. 1. C. 4. D. 5.
 3 2x
Câu 4. [ Mức độ 1] Tiệm cận ngang của đồ thị hàm số y là
 x 1
 A. y 3 . B. y 2 .C. x 2. D. x 1.
 2
Câu 5. [Mức độ 1] Tập xác định của hàm số y log3 x x 6 là 
 A.  2;3 .B. ; 2  3; .
 Trang 1 SP TỔ 10 CÁC LỖI SAI THƯỜNG GẶP-TRONG ĐỀ THI TN-THPT-NĂM HỌC 2020-2021
 C. 3;2 . D. 2;3 .
Câu 6. [Mức độ 1] Số nghiệm của phương trình ln x2 3 ln 3x 1 là
 A. 1. B. 2 . C. 3 . D. 0 .
 1
Câu 7. [Mức độ 1] Họ nguyên hàm của hàm số f x x3 3x là 
 x2
 x4 1 3x x4 1 3x
 A. C . B. .
 4 x ln 3 4 x ln 3
 x4 1 3x 2
 C. C . D. 3x2 3x ln 3 C .
 4 x ln 3 x3
Câu 8. [Mức độ 1] Cho hai hàm số f x , g x liên tục trên ¡ . Trong các mệnh đề sau, mệnh đề nào sai?
 A. f x g x dx f x dx g x dx . B. 2021f x dx 2021 f x dx .
 f x f x dx
 C. f x dx f x C , với C là hằng số.D. dx 
 g x g x dx
 2 2 4
Câu 9. [Mức độ 1] Nếu f x dx 2020 và f x dx 1 thì f x dx bằng
 4 1 1
 A. 2019 . B. 2021. C. 2021. D. 2019 .
Câu 10. [Mức độ 1] Cho hai số phức z1 3 i và z2 5 2i . 
 Tổng phần thực và phần ảo của số phức z1 z2 bằng:
 A. 1.B. 11. C. 8 3i . D. 9 . 
Câu 11. [Mức độ 1] Cho hai số phức z1 3 4i và z2 1 i . 
 Modun của z1 z2 bằng:
 A. 5 2 .B. 25 . C. 5 .D. 7 . 
Câu 12. [Mức độ 1] Cho hình chóp S.ABC đáy ABC là tam giác cân tại A , cạnh bên SA vuông góc với đáy, 
 gọi M là trung điểm cạnh BC . Góc giữa hai mặt phẳng ABC và SBC là góc nào sau đây ?
 A. S· BA. B. S·AM . C. S· CA . D. S·MA.
Câu 13. [Mức độ 1] Cho hình trụ có bán kính đáy r , chiều cao h , đường sinh l . Chọn đáp án đúng
 2 2
 A. Sxq rl . B. Sxq r h . C. Sxq 2 rl . D. Sxq 2 r h .
Câu 14. [Mức độ 1] Trong không gian với hệ tọa độ Oxyz , cho điểm M 2; 1; 3 . Hình chiếu vuông góc 
 của M trên mp Oyz là
 A. K 2; 0; 0 . B. I 0;1; 3 .C. G 2; 1; 3 . D. H 0; 1; 3 .
Câu 15. [Mức độ 1] Trong không gian với hệ tọa độ Oxyz . Phương trình tổng quát của mp P đi điểm
 M 2; 1; 3 và có n 2; 1; 3 là 
 A. 2x y 3z 14 0 . B. 2x y 3z 4 0 .
 C. 2x y 3z 14 0. D. 2x y 3z 4 0 .
Câu 16. [Mức độ 2] Cho hàm số y f x có đạo hàm trên ¡ . Hàm số y f x liên tục trên ¡ và có đồ 
 thị như trong hình vẽ sau. Hàm số f x nghịch biến trên khoảng nào? 
 Trang 2 SP TỔ 10 CÁC LỖI SAI THƯỜNG GẶP-TRONG ĐỀ THI TN-THPT-NĂM HỌC 2020-2021
 A. 2; . B. ; 1 . C. 1;1 . D. 1; .
 2
Câu 17. [Mức độ 2] Cho hàm số y f x có đạo hàm trên ¡ và f x x2 4 x 1 x 2 . Số điểm cực 
 trị của hàm số y f x là
 A. 1 . B. 2 . C. 3 . D. 4 .
 x2 3x 4
Câu 18. [Mức độ 2] Tổng số đường tiệm cận đứng và tiệm cận ngang của đồ thị hàm số y là
 x2 8x 12
 A. 1. B. 2 . C. 3 . D. 4 .
Câu 19. [ Mức độ 2] Tìm m để đồ thị hàm số y mx3 3m 2 x2 mx 3m cắt đồ thị hàm số y x 1 tại 
 ba điểm phân biệt.
 1 3 
 A. m ;1 . B. m ; .
 4 4 
 3
 C. m 0; . D. m ¡ \ 0;  .
 4
 x 1
Câu 20. [ Mức độ 2] Tìm m để đồ thị hàm số y cắt đồ thị hàm số y x 1 tại hai điểm phân biệt.
 mx 2
 A. m ;0 \ 2. B. m ¡ \ 2;0 . C. m 0; . D. m ; 2 .
Câu 21. [ Mức độ 2] Cho hàm số f x có bảng biến thiên 
 x 0 2 
 f x 0 + 0 +
 f x 
 Tìm các khoảng nghịch biến của hàm số y f 2x 4 .
 A. ;0 . B. 2; . C. 1; . D. ;2 .
Câu 22. [Mức độ 3] Cho hàm số y f x có đạo hàm y f ' x liên tục trên R . Biết rằng hàm số 
 g x f x2 2x có đúng 15 điểm cực trị. Hỏi hàm số y f x có tối đa bao nhiêu điểm cực trị 
 dương?
 A. 15. B. 7 . C. 14. D. 9 .
Câu 23. [Mức độ 2] Cho hàm số y f x liên tục trên R và có f ' x x 1 mx 1 x R với m là 
 tham số. Tìm số giá trị nguyên của tham số m trên đoạn  10;10 để hàm số có hai điểm cực trị. 
 A. 20 . B. 19. C. 10. D. 9 .
Câu 24. [Mức độ 2] Hàm số nào sau đây đồng biến trên R ? 
 Trang 3 SP TỔ 10 CÁC LỖI SAI THƯỜNG GẶP-TRONG ĐỀ THI TN-THPT-NĂM HỌC 2020-2021
 x x
 e x 2
 A. f x x . B. y . C. y 2 x . D. y log2 x .
 2 1
Câu 25. [ Mức độ 2] Cho ba số a , b , c dương và khác 1. Các hàm số y loga x , y logb x , y logc x có 
 đồ thị như hình vẽ sau
 Khẳng định nào dưới đây đúng?
 A. a c b . B. a b c . C. c b a . D. b c a .
Câu 26. [ Mức độ 2] Một người gửi ngân hàng lần đầu 100 triệu đồng với kì hạn 3 tháng, lãi suất 2% một 
 quý theo hình thức lãi kép. Sau đúng 6 tháng, người đó gửi thêm 100 triệu đồng với kì hạn và lãi suất 
 như trước đó. Sau một năm, tổng số tiền gốc và lãi của người đó là bao nhiêu (làm tròn đến hàng triệu 
 đồng)?
 A. 212 triệu. B. 216 triệu. C. 221 triệu. D. 210 triệu.
Câu 27. [ Mức độ 2] Ông An đầu tư 150 triệu đồng vào một công ty với lãi 8% một năm và lãi hàng năm được 
 nhập vào vốn ban đầu để tính lãi cho năm tiếp theo. Hỏi sau 5 năm số tiền lãi ông An rút về gần nhất 
 với số tiền nào dưới đây, nếu trong khoảng thời gian này ông An không rút tiền ra và lãi không thay 
 đổi?
 A. 220.400.000 đồng. B. 54.074.000 đồng. C. 70.398.000 đồng. D. 70.399.000 đồng.
 2 2 2
Câu 28. [ Mức độ 2] Gọi S là tập các nghiệm dương của phương trình 2x x 2x x 2 4x x 1 1. Số phần tử 
 của tập S là
 A. 1.B. 2 . C. 3 .D. 4 .
 log x 1 2 2 log 4 x log 4 x 3
Câu 29. [ Mức độ 2] Phương trình 4 2 8 có bao nhiêu nghiệm?
 A. Vô nghiệm.B. Một nghiệm.C. Hai nghiệm. D. Ba nghiệm.
 log x 1 log 11 2x 0
Câu 30. [ Mức độ 2] Tập nghiệm của bất phương trình 1 3 là
 3
 11 
 A. S 1;4 .B. S ;4.C. S 3; . D. S 1;4 .
 2 
Câu 31. [Mức độ 2] Bất phương trình log 1 x 2 log 1 7 2x có tập nghiệm là
 2 2
 5 5 5 7 5 
 A. S ; . B. S ; . C. S ; . D. S 2; .
 3 3 3 2 3 
 2
Câu 32. [Mức độ 2] Bất phương trình log4 x 3 log2 x 2 có tập nghiệm là 
 A. S 0;3 . B. S 0;4 . C. S 0;3  3;4 . D. S 3;4 .
Câu 33. [Mức độ 2] Cho f x dx x2 3x C . Tìm f e x dx .
 A. f e x dx e 2x 3e x C . B. f e x dx 2e x 3x C .
 Trang 4 SP TỔ 10 CÁC LỖI SAI THƯỜNG GẶP-TRONG ĐỀ THI TN-THPT-NĂM HỌC 2020-2021
 C. f e x dx 2e x 3e x C . D. f e x dx 2e x 3x C .
 3 
Câu 34. [ Mức độ 2] Tìm nguyên hàm F x của hàm số f x sin x , biết F 0 .
 6 
 3 1 3 3 3 1 3 3
 A. F x cos x cos3x . B. F x cos x cos3x .
 4 12 8 4 12 8
 sin4 x 1 3 1 3 3
 C. F x . D. F x cos x cos3x .
 4 64 4 4 8
 2
Câu 35. [ Mức độ 2] Cho các hàm số f x , g x xác định và liên tục trên ¡ thoả f x dx 5 và 
 3
 3 2
 3
 g x dx 9 . Tính I 2x 7 f x 6g x dx .
 2 3
 103 113 27 59
 A. I . B. I . C. I . D. I .
 2 2 2 2
 7 8
Câu 36. [ Mức độ 2] Cho hàm số f x liên tục trên ¡ thoả mãn f x dx 9 , f x dx 6 và 
 5 2
 8
 f x dx 10 . Biết F x là một nguyên hàm của f x và F 2 3 . Tính F 5 F 7 .
 7
 A. F 5 F 7 7 . B. F 5 F 7 13 . C. F 5 F 7 11. D. F 5 F 7 5 .
 9 0 9
Câu 37. [ Mức độ 2] Giả sử f x dx 37 và g x dx 16 . Khi đó, I 2 f x 3g(x) dx bằng:
 0 9 0
 A. I 26 . B. I 53 .C. I 143 . D. I 122 .
 2
Câu 38. [ Mức độ 2] Hàm số F x nào sau đây không phải là nguyên hàm của hàm số f x xex ?
 1 2 1 2
 A. F x ex 2 . B. F x ex 5.
 2 2
 1 2 1 2
 C. F x ex 2021 .D. F x ex 2020 .
 2 2 
Câu 39. [ Mức độ 2] Tìm nguyên hàm của hàm số f x x x 1 2016 .
 x 1 2018 x 1 2017
 A. f x dx C .
 2018 2017
 B. f x dx 2018 x 1 2018 2017 x 1 2017 C .
 x 1 2018 x 1 2017
 C. f x dx C .
 2018 2017
 D. f x dx 2018 x 1 2018 2017 x 1 2017 C .
 3 1
Câu 40. [ Mức độ 2] Cho .ln x.dx a.ln 3 b.ln 2 c , với a,b,c là các số hữu tỉ. Khi đó a b c bằng
 2
 2 x
 1 11 13
 A. .B. 1. C. . D. .
 3 36 24
 2
Câu 41. [ Mức độ 2] Cho hàm số y f x có đạo hàm liên tục trên ¡ . Biết f 2 5 và f x dx 3. 
 0
 Trang 5 SP TỔ 10 CÁC LỖI SAI THƯỜNG GẶP-TRONG ĐỀ THI TN-THPT-NĂM HỌC 2020-2021
 2
 Tính I x. f x dx
 0
 A. I 10 . B. I 7 . C. I 2 . D. I 7 .
Câu 42. [ Mức độ 2] Cho hàm số f x liên tục trên đoạn 0; . Biết x. f sin x dx 10 , hãy tính 
 0
 f sin x dx .
 0
 20 10
 A. . B. 10 . C. . D. 5 .
Câu 43. [ Mức độ 2] Cho H hình phẳng giới hạn bởi đồ thị hàm số y f x , trục hoành và các đường 
 thẳng x a, x b như hình vẽ bên dưới.
 y
 O a c b x
 y f x 
 Khi đó diện tích S của H là
 b c b
 A. S f x dx . B. S f x dx f x dx .
 a a c
 c b c b
 C. S f x dx f x dx . D. S f x dx f x dx .
 a c a c
Câu 44. [ Mức độ 2] Trong không gian, giả sử vật thể T nằm giữa hai mặt phẳng x 1 và x 1. Biết rằng 
 thiết diện của vật thể cắt bởi mặt phẳng vuông góc với trục Ox tại điểm có hoành độ x , x  1;1 
 là một hình vuông có cạnh bằng 2 1 x2 . Thể tích của vật thể T bằng
 16 16 8
 A. B. C. D. 
 3 3 3
Câu 45. [ Mức độ 2] Tìm tất cả các giá trị của tham số m để số phức m2 4 m 2 i là số ảo?
 A. m 0 . B. m 2 . C. m 2 . D. m 2 .
Câu 46. [Mức độ 2] Cho các số phức z1 2 3i , z2 1 5i . Tìm số phức liên hợp với số phức z1z2 .
 A. 17 7i .B. 17 7i . C. 17 7i . D. 17 7i .
 2023
Câu 47. [Mức độ 2] Tìm số phức z [(2 5i) (2 3i)] . 
 A. z 82023 i. B. z 82023 i. C. z 82023. D. z 22023 i.
Câu 48. [Mức độ 2] Tập hợp điểm biểu diễn của số phức z thỏa mãn z 3. 
 A. Hình tròn tâm O 0;0 bán kính R 3 (không kể biên).
 B. Đường tròn tâm O 0;0 bán kính R 3.
 C. Hình tròn tâm O 0;0 bán kính R 3 (kể cả biên).
 D. Đường thẳng y 3 .
 Trang 6 SP TỔ 10 CÁC LỖI SAI THƯỜNG GẶP-TRONG ĐỀ THI TN-THPT-NĂM HỌC 2020-2021
Câu 49. [Mức độ 2] Gọi H là tập hợp các điểm biểu diễn số phức z thỏa 1 z 1 2 trong mặt phẳng 
 phức. Tính diện tích hình H .
 A.3 . B. 2 . C. 4 .D. 5 .
Câu 50. [Mức độ 2] Gọi M và N lần lượt là các điểm biểu diễn của z1 , z2 trên mặt phẳng tọa độ, I là trung 
 điểm MN , O là gốc tọa độ (3 điểm O , M , N phân biệt và không thẳng hàng). Mệnh đề nào sau 
 đây là đúng?. 
 A. z1 z2 2OI . B. z1 z2 OI . 
 C. z1 z2 OM ON . D. z1 z2 2 OM ON .
Câu 51. [Mức độ 2] Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a , mặt phẳng (SAB) vuông 
 góc với mặt phẳng đáy, SA SB , góc giữa đường thẳng SC và mặt phẳng đáy bằng 45 . Tính theo a 
 khoảng cách từ điểm S đến mặt phẳng (ABCD) được kết quả
 a 3 a 5 a a 2
 A. . B. . C. .D. .
 2 2 2 2
Câu 52: [Mức độ 2] Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật tâm O , cạnh AB a , AD a 2 . 
 Hình chiếu vuông góc của S trên mặt phẳng ABCD là trung điểm đoạn OA . Góc giữa SC và mặt 
 phẳng ABCD bằng 30 . Khoảng cách từ C đến mặt phẳng SAB bằng
 3 22a 22a 3 22a 9 22a
 A. . B. . C. . D. .
 44 11 11 44
Câu 53: [Mức độ 2] Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a . Cạnh bên SB vuông góc 
 với mặt phẳng ABCD , SB a 3 . Gọi là góc giữa SD và mặt phẳng SAB . Tính tan 
 1 3 1
 A. tan . B. tan 3 . C. tan . D. tan .
 3 3 2
Câu 54: [Mức độ 2] Trong không gian cho tam giác ABC vuông cân tại A , biết AB 4a . Thể tích khối tròn 
 xoay tạo thành khi quay hình tam giác ABC quanh cạnh huyền BC bằng
 16 2 a3 32 2 a3 64 a3 64 2 a3
 A. . B. . C. . D. .
 3 3 3 3
Câu 55. [ Mức độ 2] Công thức tính thể tích khối cầu đường kính R là:
 4 4 3 1
 A. R3 . B. R3 . C. R3 . D. R3 .
 3 5 4 6
Câu 56. [Mức độ 2] Hình chữ nhật ABCD có AB 6, AD 4 . Gọi M , N, P,Q lần lượt là trung điểm của 
 bốn cạnh AB, BC,CD, DA . Cho hình chữ nhật ABCD quay quanh QN , khi đó tứ giác MNPQ tạo 
 thành vật tròn xoay có thể tích bằng 
 A. 6 . B. 4 . C. 24 . D. 8 .
Câu 57. [ Mức độ 2] Trong không gian Oxyz , cho hai điểm A 3;1; 2 , B 2; 3;5 . Điểm M thuộc đoạn 
 AB sao cho MA 2MB , tọa độ điểm M là
 7 5 8 3 17 
 A. ; ; . B. 4;5; 9 . C. ; 5; . D. 1; 7;12 .
 3 3 3 2 2 
 Trang 7 SP TỔ 10 CÁC LỖI SAI THƯỜNG GẶP-TRONG ĐỀ THI TN-THPT-NĂM HỌC 2020-2021
 x 3 y 1 2 z
Câu 58. [ Mức độ 2] Trong không gian với hệ tọa độ Oxyz , cho đường thẳng d : và mặt 
 1 2 2
 cầu S : x 1 2 y2 z 3 2 4 . Phương trình mặt phẳng P vuông góc với đường thẳng d và 
 tiếp xúc với mặt cầu S là
 A. x 2y 2z 1 0 và x 2y 2z 11 0 . B. x 2y 2z 1 0 và x 2y 2z 11 0 .
 C. x 2y 2z 1 0 và x 2y 2z 13 0 . D. x 2y 2z 13 0 và x 2y 2z 1 0.
 x y z
Câu 59. [ Mức độ 2] Trong không gian với hệ tọa độ Oxyz , cho mặt phẳng P : 1 và điểm 
 2 3 6
 A 1;1; 4 . Phương trình đường thẳng d đi qua A , song song với mặt phẳng P và cắt trụcOx là
 x 1 2t x 1 27t x 1 21t x 1 7t
 A. y 1 t . B. y 1 2t . C. y 1 2t . D. y 1 2t .
 z 4 4t z 4 8t z 4 8t z 4 8t
 x 1 y 2 z
Câu 60. [ Mức độ 2] Trong không gian với hệ tọa độ Oxyz , cho đường thẳng d : và mặt phẳng 
 2 1 3
 P : m2 1 x 2m 1 y z m2 m 3 0. Hỏi có bao nhiêu số thực m để đường thẳng d song 
 song với mặt phẳng P ?
 A. 0 . B. 1. C. 2 . D. 3 .
  
Câu 61. [Mức độ 2] Trong không gian Oxyz , cho OI 2i 2k 3 j và mặt phẳng 
 : x 2y 2z 9 0 . Phương trình mặt cầu S có tâm I và tiếp xúc với mặt phẳng là
 A. x 2 2 y 3 2 z 2 2 9 . B. x 2 2 y 3 2 z 2 2 3.
 C. x 2 2 y 3 2 z 2 2 9. D. x 2 2 y 3 2 z 2 2 9 .
Câu 62. [ Mức độ 2] Trong không gian với hệ tọa độ Oxyz , cho điểm I 2; 1; 6 và đường thẳng 
 x 1 y z 1
 : . Gọi là mặt phẳng thay đổi luôn chứa đường thẳng . Viết phương trình mặt 
 1 2 2
 cầu S có tâm I và tiếp xúc mặt phẳng sao cho mặt cầu S có bán kính lớn nhất. 
 A. x 2 2 y 1 2 z 6 2 18 . B. x 2 2 y 1 2 z 6 2 20 . 
 C. x 2 2 y 1 2 z 6 2 12 . D. x 2 2 y 1 2 z 6 2 25 .
 x 3 y z 2
Câu 63. [ Mức độ 2] Trong không gian với hệ tọa độ Oxyz , cho đường thẳng : và điểm 
 1 1 1
 M 2; 1; 0 . Phương trình mặt cầu S có tâm I thuộc đường thẳng và tiếp xúc với mặt phẳng Oxy 
 tại điểm M là
 A. x 2 2 y 1 2 z 3 2 9. B. x 2 2 y 1 2 z 3 2 9 . 
 C. x 2 2 y 1 2 z 3 2 3. D. x 2 2 y 1 2 z 3 2 9 .
Câu 64. [Mức độ 2] Từ 5 chữ số 0; 1; 2; 3; 4 có thể lập được bao nhiêu số chẵn có 4 chữ số đôi một khác 
 nhau?
 A. 60 .B. 36 . C. 72 . D. 54 .
 Trang 8 SP TỔ 10 CÁC LỖI SAI THƯỜNG GẶP-TRONG ĐỀ THI TN-THPT-NĂM HỌC 2020-2021
Câu 65. [Mức độ 2] Tổ 1 lớp 11A4 trường THPT X có 6 học sinh nữ và 5 học sinh nam. Có bao nhiêu cách 
 xếp học sinh tổ 1 lớp 11A4 trường THPT X thành một hàng dọc để học sinh nam và học sinh nữ đứng 
 liền kề nhau?
 A. 11!.B. 2!.5!.6!. C. 5!.6!. D. 11! 5!.6!.
Câu 66. [Mức độ 2] Một hộp có 3 viên bi xanh, 4 viên bi đỏ, 4 viên bi vàng và các viên bi kích cỡ như nhau. 
 Lấy ngẫu nhiên 5 viên bi. Tính xác suất 5 viên bi lấy được đủ ba màu. 
 7 26 5 20
 A. . B. . C. . D. .
 33 33 6 33
Câu 67. [ Mức độ 3] Cho x, y là hai số thực thỏa mãn x2 xy y2 1. Gọi M ,m lần lượt là giá trị lớn nhất 
 x4 y4 1
 và giá trị nhỏ nhất của P . Giá trị của A M 15m là
 x2 y2 1
 A. A 17 6 . B. A 17 6 .
 C. A 17 2 6 . D. A 17 2 6
Câu 68. [Mức độ 3] Gọi S là tập tất cả các giá trị nguyên của tham số m để bất phương trình 
 2 2
 log2 7x m 3 x 7 log2 mx 4x m có tập nghiệm là ¡ . Tổng các phần tử của S là
 A. 18. B. 25 . C. 12. D. 21.
Câu 69. [Mức độ 3] Tính thể tích của vật thể tròn xoay khi quay hình H giới hạn bởi đồ thị hàm số 
 y x3 2x2 x 2, y 4x 4 và hai đường thẳng x 1, x 1 quanh trục Ox . 
 128 4016 401 28
 A. . B. . C. . D. .
 3 105 105 3
Câu 70. [Mức độ 3] Cho z là số phức thỏa mãn z 5i z 5i 6 . Xác định phần thực của số phức z 
 sao cho giá trị của biểu thức z 5i z 5i 2 z 5i z 5i đạt giá trị lớn nhất.
 A. 3 . B. 3 . C. 5 . D. 5 .
Câu 71. [ Mức độ 3] Cắt một hình trụ bằng mặt phẳng vuông góc mặt đáy, ta được thiết diện là một hình 
 vuông có diện tích bằng 100. Biết khoảng cách từ tâm đáy hình trụ đến mặt phẳng bằng 6 . Tính 
 thể tích khối trụ.
 A. 610 . B. 61 . C. 10 . D. 10 61.
Câu 72. [ Mức độ 3] Trong không gian Oxyz , cho mặt cầu S : x 1 2 y 2 2 z 1 2 6 và hai đường 
 x 1 y 1 z 2 x 1 y 3 z 6
 thẳng d : , : . Phương trình nào dưới đây là phương trình mặt 
 1 2 2 1 2 3
 phẳng cắt mặt cầu S theo giao tuyến là một đường tròn C có bán kính bằng 1 và song song với d 
 và .
 2x y 1 0 2x y 5 0
 A. 2x y 9 0. B. . C. . D. 2x y 5 0 .
 2x y 9 0 2x y 5 0
Câu 73. [ Mức độ 3] Một hộp có 6 viên bi xanh, 5 viên bi đỏ và 4 viên bi vàng. Chọn ngẫu nhiên 5 viên bi, 
 tính xác suất sao cho 5 viên lấy ra có đủ cả ba màu.
 91 103 47 310
 A. . B. . C. . D. .
 240 405 1001 429
Câu 74. [Mức độ 3 ]Có bao nhiêu số tự nhiên m để hàm số f x x2 16 2x 2m không có điểm cực trị?
 Trang 9 SP TỔ 10 CÁC LỖI SAI THƯỜNG GẶP-TRONG ĐỀ THI TN-THPT-NĂM HỌC 2020-2021
 A. 6 . B. 5 . C. 7 . D. 8 .
 2 2
 x x 2
Câu 75. [Mức độ 4] Số giá trị nguyên của m 10;10 để phương trình 10 1 m 10 1 2.3x 1
 có đúng hai nghiệm phân biệt là 
 A. 15. B. 14. C. 16. D. 17 .
Câu 76. [Mức độ 4] Cho hàm số f x xác định và có đạo hàm f x liên tục trên đoạn 1;9, f x 0 với 
 2 2 2
 mọi x 1;9 , đồng thời f x 1 f x f x x 1 và f 1 1. Biết rằng 
   
 9
 f x dx a ln 3 b , a,b R , tính tổng S a b.
 1
 A. S 0 . B. S 1. C. S 2 . D. S 4 .
 z1 i z2 i
Câu 77. [Mức độ 4] Cho hai số phức z1 , z2 thỏa mãn 1; 2 . Giá trị nhỏ nhất của 
 z1 2 3i z2 1 i
 z1 z2 là
 A. 2 2 .B. 2 . C. 1. D. 2 1.
Câu 78. [Mức độ 4] Cho lăng trụ ABCD.A' B 'C ' D ' có đáy ABCD là hình vuông cạnh 2a, AA' A' D, khoảng 
 6a
 cách giữa hai đường thẳng CD và AB ' bằng . Tính thể tích khối chóp A'MNP trong đó 
 10
 M , N, P lần lượt là trung điểm các cạnh CD, CC ', DD '.
 A. 12a3 .B. a3 . C. 2a3 . D. 3a3 .
Câu 79. [ Mức độ 4] Trong không gian với hệ tọa độ Oxyz cho điểmA( 1;2;1) , mặt phẳng ( ) : x y z 4 0 
 và mặt cầu (S) : x 1 2 y 1 2 z 4 2 36 . Gọi (P) là mặt phẳng đi qua A , vuông góc với ( ) 
 và đồng thời (P) cắt mặt cầu (S) theo giao tuyến là một đường tròn có bán kính nhỏ nhất. Biết rằng 
 phương trình của mặt phẳng (P) khi đó là ax by cz 1 0 (a,b,c ¡ ) . Tính giá trị biểu thức 
 T 2a 3b 4c . 
 A. T 5 . B. T 3. C. T 10 . D. T 1.
Câu 80. [Mức độ 4] Lập được bao nhiêu số tự nhiên có 6 chữ số sao cho số đó có mặt đủ 4 chữ số 0;1;2;3.
 A.1110.B. 1170.C. 1230. D.810 .
 Trang 10