Đề thi thử THPT đợt 1 môn Toán 12 (Mã đề 107) - Năm học 2020- 2021 (Kèm đáp án)

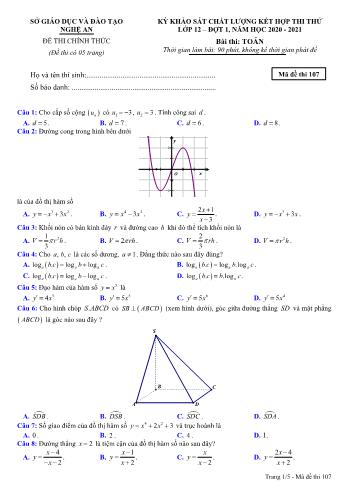
 Trang 1/5 - Mã đề thi 107 
SỞ GIÁO DỤC VÀ ĐÀO TẠO 
NGHỆ AN 
ĐỀ THI CHÍNH THỨC 
(Đề thi có 05 trang) 
KỲ KHẢO SÁT CHẤT LƯỢNG KẾT HỢP THI THỬ 
LỚP 12 – ĐỢT 1, NĂM HỌC 2020 - 2021 
Bài thi: TOÁN 
Thời gian làm bài: 90 phút, không kể thời gian phát đề 
 Họ và tên thí sinh:.................................................................... 
 Số báo danh: ............................................................................ 
Câu 1: Cho cấp số cộng nu có 1 3u , 2 3u . Tính công sai d . 
 A. 5d . B. 7d . C. 6d . D. 8d . 
Câu 2: Đường cong trong hình bên dưới 
là của đồ thị hàm số 
 A. 3 23y x x . B. 4 23y x x . C. 
2 1
3
x
y
x
. D. 3 3y x x . 
Câu 3: Khối nón có bán kính đáy r và đường cao h khi đó thể tích khối nón là 
 A. 2
1
3
V r h . B. 2V rh . C. 
2
3
V rh . D. 2V r h . 
Câu 4: Cho , ,a b c là các số dương, 1a . Đẳng thức nào sau đây đúng? 
 A. log . log loga a ab c b c . B. log . log .loga a ab c b c . 
 C. log . log loga a ab c b c . D. log . .lo.... 36a . 
Câu 20: Số điểm cực trị của hàm số 4 22 3y x x là 
 A. 3 . B. 2 . C. 0 . D. 1. 
Câu 21: Một khối cầu có bán kính bằng 2 , một mặt phẳng cắt khối cầu đó theo một hình tròn có diện tích 
là 2 . Khoảng cách từ tâm khối cầu đến mặt phẳng bằng 
 A. 
2
2
. B. 1. C. 2 . D. 
2
4
. 
4
2
y
x
O
 Trang 3/5 - Mã đề thi 107 
Câu 22: Cho hàm số y f x có bảng biến thiên: 
Số tiệm cận đứng và tiệm cận ngang của đồ thị hàm số y f x là 
 A. 3 . B. 0 . C. 1. D. 2 . 
Câu 23: Cho lăng trụ .ABC A B C có đáy ABC là tam giác đều cạnh 2a , 2AA a . Biết rằng hình chiếu 
vuông góc của A lên ABC là trung điểm BC . Thể tích của khối lăng trụ .ABC A B C là 
 A. 3 3a . B. 
32 3
3
a
. C. 
3 6
2
a
. D. 
34 2
3
a
. 
Câu 24: Biểu thức T 
1
10 53 15
2
3 233
.
.
a a a
a a a
 (với 0, 1a a ) rút gọn là 
 A. T 1a . B. T 
1
1a 
. C. T 
1
1a 
. D. T 
3
1
1a 
. 
Câu 25: Với giá trị nào của m thì hàm số 3 21 1y x m x mx đạt cực tiểu tại 1x ? 
 A. 0m . B. 1m . C. 1m . D. 2m . 
Câu 26: Tất cả các giá trị của m sao cho hàm số 3 23 2y x mx m nghịch biến trên khoảng 0 ; 6 là 
 A. 3m . B. 0 6m . C. 6m . D. 3m . 
Câu 27: Một hộp chứa 7 quả cầu xanh, 8 quả cầu vàng. Chọn ngẫu nhiên 3 quả. Xác suất để 3 quả được 
chọn có ít nhất 2 quả xanh là 
 A. 
8
65
. B. 
6
11
. C. 
29
65
. D. 
7
11
. 
Câu 28: Tâm các mặt của hình lập phương tạo thành các đỉnh của khối đa diện nào sau đây ? 
 A. Khối bát diện đều. B. Khối lăng trụ tam giác đều. 
 C. Khối tứ diện đều. D. Khối chóp lục giác đều. 
Câu 29: Cho hình chóp .S ABCD có đáy là hình vuông, đường chéo 2BD a . Tam giác SAC vuông cân tại S 
và nằm trong mặt phẳng vuông góc với đáy. Thể tích của khối cầu ngoại tiếp hình chóp đó là 
 A. 
34
3
a 
. B. 34 3a . C. 3a . D. 34 a . 
Câu 30: Gọi M , C , Đ thứ tự là số mặt, số cạnh, số đỉnh của hình lăng trụ ngũ giác. Khi đó S M C Đ 
bằng 
 A. 12S . B. 2S . C. 18S . D. 14S . 
Câu 31: Số nghiệm của phương trình 23 3log 6 log 2 1x x là 
 A. 1....cực trị đó. 
 A. 1m . B. 5m . C. 2m . D. 3m . 
Câu 42: Cho hình nón có chiều cao là 10a . Một mặt phẳng P đi qua đỉnh S của hình nón và cắt đường tròn 
đáy của hình nón tại hai điểm A , B sao cho tam giác SAB có diện tích bằng 
240 23
3
a
. Biết rằng góc giữa 
mặt phẳng P và mặt đáy của hình nón là 60 . Thể tích của khối nón được giới hạn bởi hình nón đã cho bằng 
 A. 
3640
3
a 
. B. 
31280
3
a 
. C. 
3320
3
a 
. D. 
3160
3
a 
. 
Câu 43: Một loại kẹo có hình dạng là khối cầu với bán kính bằng 1cm được đặt trong vỏ kẹo có hình dạng là 
hình chóp tứ giác đều (các mặt của vỏ tiếp xúc với kẹo ). Biết rằng khối chóp đều tạo thành từ vỏ kẹo đó có thể 
tích bé nhất, tính tổng diện tích tất cả các mặt của vỏ kẹo. 
 A. 264 cm . B. 236 cm . C. 232 cm . D. 224 cm . 
Câu 44: Đặt 2log 5 a , tính giá trị của 4log 1250 theo a . 
 A. 
1 4
2
a 
. B. 2 1 4a . C. 
1 4
2
a 
. D. 2 1 4a . 
Câu 45: Cho các số thực ,a b thỏa mãn: 2 2 1a b , tổng giá trị lớn nhất và giá trị nhỏ nhất của biểu thức 
2 22 22 2 2 2 1P a a a a b bằng 
 A. 3 . B. 
13 4 3
4
. C. 3 . D. 
12 2 3
3
. 
 Trang 5/5 - Mã đề thi 107 
Câu 46: Cho hình chóp .S ABCD có đáy ABCD là hình thoi tâm O . Biết 2 3AC a , 2BD a , 2SD a 
và SO vuông góc với mặt phẳng đáy. Khoảng cách giữa hai đường thẳng AB và SD bằng 
 A. 
21
3
a . B. 
2 21
3
a . C. 
21
7
a . D. 
2 21
7
a . 
Câu 47: Người ta thiết kế 1 cái ly thủy tinh dùng để uống nước có dạng hình trụ như hình vẽ, biết rằng ở mặt 
ngoài ly có chiều cao là 15cm và đường kính đáy là 8 cm , độ dày thành ly là 2 mm , độ dày đáy là 1cm . Hãy 
tính thể tích lượng thủy tinh cần để làm nên cái ly đó (kết quả gần đúng nhất). 
 A. 3753982, 24 mm . B. 3118877,87 mm . C. 3753600 mm . D. 3118817,62 mm . 
Câu 48: Điều kiện để phương trình 212 3 0x x m có nghiệm là [ ; ]m a b , khi đó 2a b bằng 
 A. 10 . B. 6 . C. 2 . D. 8 . 
Câu 49: Cho hình chóp ngũ giác đều có tổng diện tích tất cả các mặt là 9S . Giá trị lớn nhất của thể