Đề thi thử lần 1 tốt nghiệp THPT môn Toán Lớp 12 - Năm học 2020-2021 - Sở GD&ĐT Ninh Bình (Có đáp án)

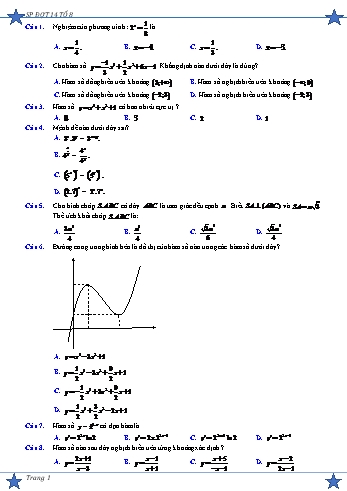
 SP ĐỢT 14 TỔ 8 
 1
Câu 1. Nghiệm của phương trình: 2x là
 8
 1 1
 A. x . B. x 4. C. x . D. x 3.
 4 3
 1 1
Câu 2. Cho hàm số y x3 x2 6x 1. Khẳng định nào dưới đây là đúng?
 3 2
 A. Hàm số đồng biến trên khoảng 3; .B. Hàm số nghịch biến trên khoảng ;0 .
 C. Hàm số đồng biến trên khoảng 2;3 .D. Hàm số nghịch biến trên khoảng 2;3 .
Câu 3. Hàm số y x4 x2 1 có bao nhiêu cực trị ?
 A. 0 .B. 3 .C. 2 .D. 1.
Câu 4. Mệnh đề nào dưới đây sai?
 A. 3x.3y = 3x+ y.
 x 4x
 B. 4y = .
 4y
 y x
 C. (5x ) = (5y ) .
 x
 D. (2.7) = 2x.7x.
Câu 5. Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh a . Biết SA  (ABC) và SA a 3 . 
 Thể tích khối chóp S.ABC là:
 3a3 a3 3a3 3a3
 A. .B. C. D. .
 4 4 6 4
Câu 6. Đường cong trong hình bên là đồ thị của hàm số nào trong các hàm số dưới đây?
 y
 3
 1
 O
 1 3 x
 A. y x3 3x2 1
 1 9
 B. y x3 3x2 x 1
 2 2
 1 9
 C. y x3 3x2 x 1
 2 2
 1 3
 D. y x3 x2 2x 1
 2 2
Câu 7. Hàm số y = 22 x có đạo hàm là
 A. y 22x ln 2 .B. y 2x.22x 1 .C. y 22x 1 ln 2 .D. y 22x 1 .
Câu 8. Hàm số nào sau đây nghịch biến trên từng khoảng xác định ?
 2x 1 x 1 x 5 x 2
 A. y B. y C. y D. y 
 x 3 x 1 x 1 2x 1
 Trang 1 SP ĐỢT 14 TỔ 8 
Câu 9. Cho hình trụ có chiều cao bằng 5 và đường kính đáy bằng 8 . Tính diện tích xung quanh của hình 
 trụ đó?
 A. 20 . B. 40 .C. 160 . D. 180 .
Câu 10. Cho hình lăng trụ có diện tích đáy là 3a2 , độ dài đường cao bằng 2a . Thể tích khối lăng trụ 
 bằng:
 A. 6a3 .B. 3a3 C. 2a3 D. a3 .
Câu 11. Tập nghiệm của bất phương trình log3 (x 1) 1?
 A. (1;4] B. ( ;4) C. ( ;4] D. (0;4]
Câu 12. Cho hàm số y f x có bảng biến thiên như sau
 x 0 1 
 y 0 
 2 
 y
 4 2
 Tổng số đường tiệm cận đứng và ngang của đồ thị hàm số là
 A. 1.B. 3. C. 4 .D. 2 .
Câu 13. Công thức tính diện tích mặt cầu bán kính r là
 4 3
 A. S r 2 .B. S 4 r 2 . C. S r3 . D. S r 2 .
 3 4
Câu 14. Họ tất cả các nguyên hàm của hàm số f (x) e3x là
 e3x
 A. 3e3x C .B. F(x) C .
 3ln3
 1
 C. F(x) e3x C . D. e3x C .
 3
Câu 15. Cho hàm số y f x có đồ thị như hình vẽ bên. Số nghiệm của phương trình 3 f x 5 0 là:
 A. 4 .B. 5 . C. 2 .D. 3 .
 x 1
Câu 16. Cho hàm số y . Tính tổng giá trị lớn nhất M và giá trị nhỏ nhất m của hàm số trên đoạn 
 2x 1
 0;2 .
 Trang 2 SP ĐỢT 14 TỔ 8 
 1 1 4
 A. M m .B. M m . C. M m .D. M m 1.
 5 5 5
Câu 17. Hãy tìm tập xác định D của hàm số y ln x2 2x 3 .
 A. D ( 1;3) .B. D ; 1  3; .
 C. D ; 13; . D. D [ 1;3].
Câu 18. Với mọi a, b, x là các số thực dương thỏa mãn log2 x 5log2 a 3log2 b. Mệnh đề nào dưới đây 
 đúng?
 A. x 3a 5b. B. x a5b3. C. x a5 b3. D. x 5a 3b.
 32 5
Câu 19. Một hình nón có thể tích V và bán kính hình tròn đáy bằng 4 . Diện tích xung quanh 
 3
 của hình nón bằng
 A. 24 5 . B. 48 . C. 24 .D. 12 5 .
 x
Câu 20. Cho I dx . Nếu đặt t x 1 thì I f t dt , trong đó f t bằng:
 1 x 1 
 A. f t 2t 2 2t .B. f t t 2 t .C. f t t 1.D. f t t 2 t .
Câu 21. Cho hàm số y 2x3 3x2 m . Trên  1;1 hàm số có giá trị nhỏ nhất là 1. Tìm m .
 A. m 5 .B. m 3 .C. m 6 . D. m 4 .
Câu 22. Cho khối trụ có đường cao gấp đôi bán kính đáy. Một mặt phẳng qua trục của khối trụ cắt khối 
 trụ theo thiết diện là một hình chữ nhật có diện tích bằng16a2 . Thể tích của khối trụ đã cho tính 
 theo abằng:
 16 32
 A. 4 a3 . B. a3 . C. 16 a3 .D. a3 .
 3 3
Câu 23. Biết rằng đường thẳng y 2x 3 cắt đồ thị hàm số y x3 x2 2x 3 tại hai điểm phân biệt A 
 và B , biết điểm B có hoành độ âm. Hoành độ điểm B bằng
 A. 0 .B. 5 . C. 1. D. 2 .
Câu 24. Cho hình lập phương ABCD.A B C D có diện tích mặt chéo ACC A bằng 2 2a2 . Thể tích của 
 khối lập phương ABCD.A B C D là
 A. 16 2a3 . B. 2 2a3 . C. 8a3 . D. a3 .
Câu 25. Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật, mặt bên (SAD) là tam giác đều cạnh 
 4a và nằm trong mặt phẳng vuông góc với mặt phẳng ABCD . Góc giữa mặt phẳng (SBC) và 
 mặt phẳng ABCD là 300 . Thể tích khối chóp S.ABCD là:
 A. 24 3a3 .B. 16 3a3 . C. 4 3a3 D. 48 3a3 .
Câu 26. Cho T là tổng tất cả các nghiệm của phương trình 4x 5.2x 6 0. Tính giá trị của T .
 A. T log 2 3 .B. T 5 .C. T log2 6 .D. T 1.
Câu 27. Số nghiệm của phương trình log2 x log2 x 1 1 là
 A. 1.B. 2 . C. 3 .D. 0
 x
 x x x æ2ö
Câu 28. Cho bất phương trình 12.9 - 35.6 + 18.4 0 , bất phương trình 
 èç3ø÷
 trở thành
 A. 12t 2 35t 18 0 .B. 12t 2 35t 18 0 .
 C. 18t 2 35t 12 0 . D. 18t 2 35t 12 0 .
 Trang 3 SP ĐỢT 14 TỔ 8 
Câu 29. Trong không gian cho hình chữ nhật ABCD có AB a , AC a 5 . Diện tích xung quanh của 
 hình trụ thu được khi quay hình chữ nhật ABCD quanh trục AB bằng
 2 a2
 A. 8 a2 . B. 4 a2 . C. 2 a2 . D. .
 3
Câu 30. Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật với AB a, AD 2a . Biết SA vuông 
 góc với mặt phẳng đáy và SB a 5 . Góc giữa đường thẳng SD và mặt phẳng ABCD bằng
 A. 30o .B. 90o . C. 60o .D. 45o .
 2
Câu 31. Cho hàm số y f x có đạo hàm f x x x 1 2x 3 . Hàm số đã cho có bao nhiêu điểm 
 cực trị?
 A. 1.B. 3 . C. 0 .D. 2 .
Câu 32. Trong không gian cho đoạn thẳng AB có độ dài bằng 6 . Điểm M di động trong không gian sao 
 cho diện tích tam giác MAB bằng 12 và hình chiếu vuông góc của M lên AB nằm trong đoạn 
 AB . Quỹ tích các điểm M tạo thành một phần của mặt tròn xoay. Diện tích phần mặt tròn xoay 
 đó bằng
 A. 48 .B. 24 2 .C. 36 .D. 80 .
 x
Câu 33. Cho x, y là các số thực dương thỏa mãn log 4 x log3 y log2 2x 3y . Giá trị của bằng:
 3 y
 9 3 2 4
 A. B. log C. log . D. .
 4 3 2 2 3 9
 2
Câu 34. Cho bất phương trình log2 2x 2 m 1 log2 x 2 0 . Tìm tất cả các giá trị của tham số m 
 để bất phương trình có nghiệm thuộc khoảng 2; .
 3 3 
 A. m ;0 . B. m ; .C. m 0; . D. m ;0 .
 4 4 
 x m
Câu 35. Tìm tất cả các giá trị m sao cho hàm số y đồng biến trên các khoảng xác định.
 x 2
 A. m 2 . B. m 2 .C. m 2 .D. m 2 .
 mx2 1
Câu 36. Có bao nhiêu giá trị m để đồ thị hàm số y có đúng hai đường tiệm cận?
 x2 3x 2
 A. 4 .B. 3 . C. 2 .D. 1.
Câu 37. Cho hình lăng trụ ABC.A' B 'C ', đáy là tam giác vuông tại A và AC a . Biết hình chiếu vuông 
 góc của B ' lên mặt phẳng ABC là trung điểm H của BC . Góc giữa ABB ' A' với mặt 
 ABC là 60o . Gọi G là trọng tâm tam giác B 'CC '. Tính khoảng cách từ G đến ABB ' A' .
 3 3a 3a 3a 3a
 A. .B. .C. .D. 
 4 4 2 3
Câu 38. Khi xây nhà, cô Ngọc cần xây một bể đựng nước mưa có thể tích V 6m3 dạng hình hộp chữ 
 nhật với chiều dài gấp 3 lần chiều rộng, đáy và nắp và các mặt xung quanh đều được đổ bê tông, 
 2
 cốt thép. Phần nắp bể để hở một khoảng hình vuông có diện tích bằng diện tích nắp bể. Biết 
 9
 rằng chi phí cho 1m2 bê tông cốt thép là 1.000.000 đ. Tính chi phí thấp nhất mà cô Ngọc phải trả 
 khi xây bể ( làm tròn đến hàng trăm nghìn ) ?
 A. 12.600.000d. B. 21.000.000d. C. 20.900.000d .D. 21.900.000d .
 Trang 4 SP ĐỢT 14 TỔ 8 
Câu 39. Cắt hình nón đỉnh S bởi mặt phẳng đi qua trục ta được một tam giác vuông cân có cạnh huyền 
 bằng a 2 . Gọi BC là dây cung của đường tròn đáy hình nón sao cho mặt phẳng SBC tạo với 
 mặt đáy một góc 60 . Tính diện tích của tam giác SBC .
 2a2 2a2 a2 3a2
 A. S .B. S .C. S .D. S .
 SBC 2 SBC 3 SBC 3 SBC 3
 1
Câu 40. Hàm số y x3 mx2 m2 m 1 x 1 đạt cực đại tại điểm x 1 khi
 3
 A. m 1 .B. m 1 C. m 1 .hoặc m 2 D. m 2 .
Câu 41. Cho hàm số y f x có đạo hàm trên ¡ và có bảng xét dấu f x như sau
 Hỏi hàm số y f x2 2x có bao nhiêu điểm cực tiểu?
 A. 1.B. 4.C. 3.D. 2.
 ax 1
Câu 42. Cho hàm số f x a,b,c ¡ có bảng biến thiên như sau:
 bx c
 Trong các số a,b,c có bao nhiêu số dương ?
 A. 2 B. 1 C. 0 D. 3
Câu 43. Hình vẽ bên là đồ thị của hàm số y x3 3x2 .Tìm tất cả các giá trị của tham số m
 để phương trình 3x2 3 m x3 có hai nghiệm thực phân biệt.
 m 1
 A. 1 m 1. B. .
 m 1
 m 1
 C. . D. m 1.
 m 3
Câu 44. Cho hàm số f x x2 2x 1. Có bao nhiêu giá trị nguyên của tham 
 số m để giá trị lớn nhất của hàm số g x f 2 x 2 f x m trên 
 đoạn  1;3 bằng 8
 A. 5 . B. 4 .
 C. 3 .D. 2 .
 Trang 5 SP ĐỢT 14 TỔ 8 
Câu 45. Cho lăng trụ ABC.A B C có diện tích đáy bằng 12 và chiều cao 
 bằng 6 . Gọi M , N lần lượt là trung điểm của CB,CA và P,Q, R lần 
 lượt là tâm các hình bình hành ABB A , BCC B ,CAA C . Thể tích 
 của khối đa diện PQRABMN bằng
 A. 42 .B. 14.
 C.18.D. 21.
Câu 46. Cho hàm số bậc ba có đồ thị như hình vẽ.
 Có bao nhiêu giá trị nguyên của tham số m  5;5 để phương trình 
 log3 f x 1 log2 f x 1 2m 8 log f x 1 2m 0 có 
 2 2 1 
 2
 nghiệm x 1;1 ?
 A. 7.B. 5.
 C. Vô số.D. 6.
Câu 47. Có tất cả bao nhiêu giá trị nguyên của y sao cho tương ứng mỗi y luôn tồn 
 tại không quá 63
 2 2
 số nguyên x thỏa mãn điều kiện log2020 x y log2021 y y 64 log4 x y 
 A. 301 B. 302 C. 602 D. 2
 1
Câu 48. Cho hàm số f x x . Cho điểm M a;b sao cho có đúng hai tiếp tuyến của đồ thị hàm số 
 x
 y f x đi qua M , đồng thời hai tiếp tuyến này vuông góc với nhau, biết điểm M luôn thuộc 
 một đường tròn cố định, bán kính của đường tròn đó là.
 A. 2 .B. 4 . C. 1. D. 2 .
Câu 49. Cho f x là một hàm số có đạo hàm liên tục trên ¡ và 
 hàm số g x f x 2 3x 1 có đồ thị như hình vẽ sau:
 Hàm số f x 1 nghịch biến trên khoảng nào dưới 
 đây?
 1 
 A. ;0 .B. 2;3 .
 4 
 C. 0;1 .D. 3; .
Câu 50. Cho tứ giác lồi có 4 đỉnh nằm trên đồ thị hàm số 
 y ln x , với hoành độ các đỉnh là các số nguyên dương 
 21
 liên tiếp. Biết diện tích của tứ giác đó là ln . Khi đó hoành độ của đỉnh nằm thứ 3 từ trái sang 
 20
 là
 A. 5 .B. 11.C. 9 . D. 7 .
 Trang 6 SP ĐỢT 14 TỔ 8 
 BẢNG ĐÁP ÁN
 1D 2C 3D 4B 5B 6B 7C 8A 9B 10A
 11A 12D 13B 14D 15A 16C 17B 18B 19C 20A
 21D 22C 23C 24B 25B 26C 27A 28C 29B 30D
 31D 32A 33A 34B 35B 36C 37D 38B 39B 40D
 41A 42D 43A 44D 45D 46A 47C 48A 49C 50D
 1
Câu 1. [2D2-5.1-1] Nghiệm của phương trình: 2x là
 8
 1 1
 A. x . B. x 4. C. x . D. x 3.
 4 3
 Lời giải
 Tác giả: Nguyễn Minh Thúy; Fb:ThuyMinh
 Chọn D
 1
 Ta có: 2x 2x 2 3 x 3. Chọn D
 8
 1 1
Câu 2. [2D1-1.1-2] Cho hàm số y x3 x2 6x 1. Khẳng định nào dưới đây là đúng?
 3 2
 A. Hàm số đồng biến trên khoảng 3; .B. Hàm số nghịch biến trên khoảng ;0 .
 C. Hàm số đồng biến trên khoảng 2;3 .D. Hàm số nghịch biến trên khoảng 2;3 .
 Lời giải
 Chọn C
 2 x 3
 y ' x x 6, y ' 0 , ta có bảng xét dấu:
 x 2
 Dựa vào bảng xét dấu chọn C.
Câu 3. [2D1-2.1-1] Hàm số y x4 x2 1 có bao nhiêu cực trị ?
 A. 0 .B. 3 .C. 2 .D. 1.
 Lời giải
 Chọn D
 Hàm số y x4 x2 1 có hệ số a 1, b 1, c 1
 Ta có a.b 1 0
 Vậy hàm số có 1 điểm cực trị .
Câu 4. [2D2-1.2-1] Mệnh đề nào dưới đây sai?
 A. 3x.3y = 3x+ y.
 x 4x
 B. 4y = .
 4y
 y x
 C. (5x ) = (5y ) .
 x
 D. (2.7) = 2x.7x.
 Lời giải
 Trang 7 SP ĐỢT 14 TỔ 8 
 Chọn B
 x 1 4x
 4y = (4x )y ¹ = 4x- y
 4y
Câu 5. [2H1-3.2-1] Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh a . Biết SA  (ABC) và 
 SA a 3 . Thể tích khối chóp S.ABC là:
 3a3 a3 3a3 3a3
 A. . B. C. D. .
 4 4 6 4
 Lời giải
 Chọn B
 S
 a 3
 A C
 a
 B
 a2 3
 Ta có diện tích tam giác ABC là: 
 4
 1 a2 3 a3
 Thể tích khối chóp S.ABC là: V . .a 3 
 3 4 4
Câu 6. [2D1-5.1-1] Đường cong trong hình bên là đồ thị của hàm số nào trong các hàm số dưới đây?
 y
 3
 1
 O
 1 3 x
 A. y x3 3x2 1
 1 9
 B. y x3 3x2 x 1
 2 2
 1 9
 C. y x3 3x2 x 1
 2 2
 1 3
 D. y x3 x2 2x 1
 2 2
 Lời giải
 Trang 8 SP ĐỢT 14 TỔ 8 
 FB tác giả: Lưu Thị Hương Quỳnh
 Chọn B
 Thay x 1 y 3
Câu 7. [2D2-4.2-1] Hàm số y = 22 x có đạo hàm là
 A. y 22x ln 2 .B. y 2x.22x 1 .C. y 22x 1 ln 2 .D. y 22x 1 .
 Lời giải
 Chọn C
 Ta có y¢= 2.22 x ln 2 = 22 x+ 1.ln 2 .
Câu 8. [2D1-1.1-1] Hàm số nào sau đây nghịch biến trên từng khoảng xác định ?
 2x 1 x 1 x 5 x 2
 A. y B. y C. y D. y 
 x 3 x 1 x 1 2x 1
 Lời giải
 Chọn A
 2x 1
 Xét hàm số y .
 x 3
 7 2x 1
 Ta có y ' 0 nên hàm số y nghịch biến trên từng khoảng xác định của nó.
 x 3 2 x 3
Câu 9. [2H2-1.2-1] Cho hình trụ có chiều cao bằng 5 và đường kính đáy bằng 8 . Tính diện tích xung 
 quanh của hình trụ đó?
 A. 20 . B. 40 .C. 160 . D. 180 .
 Lời giải
 Chọn B
 8
 Bán kính đáy của hình trụ là 4 .
 2
 Diện tích xung quanh của hình trụ là Sxq 2 rl 2 .4.5 40 .
Câu 10. [2H2-1.1-1] Cho hình lăng trụ có diện tích đáy là 3a2 , độ dài đường cao bằng 2a . Thể tích khối 
 lăng trụ bằng:
 A. 6a3 .B. 3a3 C. 2a3 D. a3 .
 Lời giải
 Chọn A
 Ta có thể tích khối lăng trụ là: V 3a2.2a 6a3
Câu 11. [2D2-6.1-1] Tập nghiệm của bất phương trình log3 (x 1) 1?
 A. (1;4] B. ( ;4) C. ( ;4] D. (0;4]
 Lời giải
 FB tác giả: Dung Nguyễn
 Chọn A
 log3 (x 1) 1 0 x 1 3 1 x 4
Câu 12. [2D1-4.1-1] Cho hàm số y f x có bảng biến thiên như sau
 Trang 9 SP ĐỢT 14 TỔ 8 
 x 0 1 
 y 0 
 2 
 y
 4 2
 Tổng số đường tiệm cận đứng và ngang của đồ thị hàm số là
 A. 1.B. 3. C. 4 .D. 2 .
 Lời giải
 Chọn D
 Dựa vào BBT ta có lim f x 2 suy ra TCN của đồ thị hàm số là y 2 .
 x 
 lim f x suy ra TCĐ của đồ thị hàm số là x 0 .
 x 0 
Câu 13. [2H2-2.2-1] Công thức tính diện tích mặt cầu bán kính r là
 4 3
 A. S r 2 .B. S 4 r 2 . C. S r3 . D. S r 2 .
 3 4
 Lời giải
 Chọn B
 Công thức tính diện tích mặt cầu bán kính r là S 4 r 2.
Câu 14. [2D3-1.1-1] Họ tất cả các nguyên hàm của hàm số f (x) e3x là
 e3x
 A. 3e3x C . B. F(x) C .
 3ln3
 1
 C. F(x) e3x C . D. e3x C .
 3
 Lời giải
 Chọn D
 1
 Ta có: e3xdx e3x C .
 3
Câu 15. [2D1-5.4-1] Cho hàm số y f x có đồ thị như hình vẽ bên. Số nghiệm của phương trình 
 3 f x 5 0 là:
 Trang 10