Đề ôn tập kiểm tra đợt 9 môn Toán Lớp 12 - Tổ 4 - Chủ đề: Hàm hợp - Năm học 2020-2021 (Có đáp án)

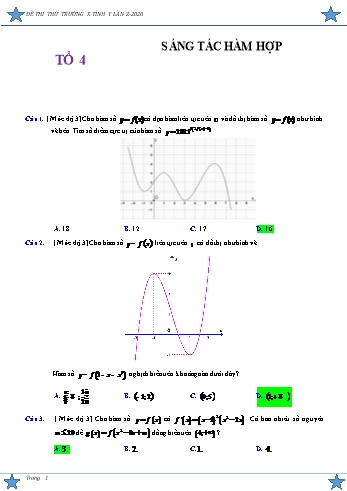
 ĐỀ THI THỬ TRƯỜNG X TỈNH Y LẦN Z-2020 
 SÁNG TÁC HÀM HỢP
 TỔ 4
Câu 1. [ Mức độ 3] Cho hàm số y f (x) có đạo hàm liên tục trên ¡ và đồ thị hàm số y f (x) như hình 
 vẽ bên. Tìm số điểm cực trị của hàm số y 2021f 2 f x 1 .
 A. 18. B. 12. C. 17. D. 16.
Câu 2. [ Mức độ 3] Cho hàm số y = f (x) liên tục trên ¡ có đồ thị như hình vẽ
 Hàm số y = f (1- x- x3 ) nghịch biến trên khoảng nào dưới đây?
 æ 1ö
 A. ç- ¥ ; ÷. B. (- 1;2). C. (0;5). D. (1;+ ¥ ).
 èç 2ø÷
Câu 3. [ Mức độ 3] Cho hàm số y f x có f ' x x 1 2 x2 2x . Có bao nhiêu số nguyên 
 m 20 để g x f x2 8x m đồng biến trên 4; ? 
 A.3 . B. 2. C.1. D. 4. 
 Trang 1 ĐỀ THI THỬ TRƯỜNG X TỈNH Y LẦN Z-2020 
Câu 4. [ Mức độ 3] Cho hàm số y f x có đạo hàm f ' x x2 x 4 x2 2mx 9 với 
 x ¡ . Số giá trị nguyên âm của m để hàm số g x f x2 3x 4 đồng biến trên 
 1; ? 
 A. 1. B. 3 . C. 2 . D. 4 .
Câu 5. [ Mức độ 3] Cho hàm số y f x liên tục trên ¡ có f ' x ex x . Hàm số 
g x f x 1 f 2 x đồng biến trên khoảng nào sau đây.
 A. ;1 . B. 2; . C. 1; . D. ;2 .
Câu 6. [ Mức độ 3] Cho hàm số f x có đạo hàm liên tục trong khoảng 0; và có bảng xét dấu 
 đạo hàm như sau:
 x 0 1 4 + ¥
 f ¢(x) - 0 + 0 -
 Hàm số g x f ln x 1 2 đồng biến trong khoảng nào sau đây?
 3 1 1 1 1 
 A. 1;e . B. 3 ; 2 .C. 0;1 .D. 2 ; .
 e e e e 
Câu 7. [ Mức độ 3] Cho hàm số f x x4 4 m2 x 2020 và g x x3 5x2 2020x 2021. 
 Có bao nhiêu giá trị nguyên dương của m để h x g f x đồng biến trên 2; .
 A. 13. B. 12. C. 7 . D. 6 .
Câu 8. [ Mức độ 4] Cho đồ thị hàm số y f '(x) như hình vẽ. Tìm các khoảng đồng biến của hàm số:
y g(x) f (3x 1) x3 3x2 1 .
 A. . ; 4 B. ; 4 và 1;5 
 C. ( 4; 1) và (2;5) . D. (0;2) và ( ; 1).
 Trang 2 ĐỀ THI THỬ TRƯỜNG X TỈNH Y LẦN Z-2020 
Câu 9. [ Mức độ 4 ] Cho hàm số g x f 1 x có đạo hàm 
 2021 2020 2
 g ' x 3 x 2 x x m 2 x 3m 6 với mọi x ¡ . Có bao nhiêu số nguyên 
 dương m để hàm số f x nghịch biến trên khoảng 0; .
 A. 0 . B. 1. C. 2 . D. 3.
Câu 10. [Mức độ 3] Cho hàm số f x có đạo hàm f (x) (x 1)2 x2 4x .Có bao nhiêu giá trị 
 nguyên dương của tham số m để hàm số g(x) f 2x2 12x m có đúng 5 điểm cực trị ?
 A.18. B.17. C.16. D.19.
Câu 11. [ Mức độ 3] Cho hàm số y f x có đạo hàm liên tục trên ¡ và f 0 0; f 4 4 . Biết 
 hàm y f x có đồ thị như hình vẽ bên. Tìm số điểm cực trị của hàm số g x f x2 2x .
 A. 1. B. 2. C. 5. D. 3.
Câu 12. Cho hàm số f x có đạo hàm liên tục trên ¡ . Hàm số f ' x có đồ thị là đường cong trong 
 hình vẽ dưới đây. 
 2 2
 Số điểm cực tiểu của hàm số g x f 2x x 2x x là
 A.3.B. 2 .C. 5.D. 4 .
Câu 13. [Mức độ 3] Cho hàm số y f x xác định trên ¡ và hàm số y f x có đồ thị như hình vẽ. Tìm 
 số điểm cực trị của hàm số g x f x2 3 2020x2 .
 Trang 3 ĐỀ THI THỬ TRƯỜNG X TỈNH Y LẦN Z-2020 
 y
 2
 -2 1 x
 O
 A. 1.B. 2. C. 3. D. 0 .
Câu 13.1 [Mức độ 4] Cho hàm số f x . Hàm số y f x có đồ thị như hình bên. 
 2 1 
 Hàm số g x f x 2ln x có bao nhiêu điểm cực trị
 2 
 A. 4.B. 5. C. 6 . D. 7 .
Câu 14. [ Mức độ 3] Cho hàm số y f x liên tục trên ¡ . Đồ thị hàm số y f x như hình vẽ sau:
 Số điểm cực trị của hàm số y f x2 2x 2021 là
 A.1.B. 3 .C. 4 . D.5 .
Câu 15. [Mức độ 3]Cho hàm số y f x có f '(x) x(x 1)2 (x 2) Số điểm cực đại của hàm số 
 g(x) f (x2 x) bằng:
 Trang 4 ĐỀ THI THỬ TRƯỜNG X TỈNH Y LẦN Z-2020 
 A. 1.B. 3 . C. 4 D. 2 .
Câu 16. [ Mức độ 3]Cho hàm số y f x có đạo hàm liên tục trên ¡ và bảng xét dấu đạo hàm như 
 sau:
 Số điểm cực tiểu của hàm số g x 3 f x4 4x2 6 2x6 3x4 12x2 là:
 A. 4 .B. 3 .C. 0 . D. 2 .
 2x
Câu 17. [Mức độ 4] Cho hàm số y f x . Số giá trị của tham số thực m  10;10để phương 
 2x 8
 trình: f cos2x 2sin x.cos x 1 f 2m2 7m 3 x 3m 9 1 vô nghiệm.
 A. 1. B. 2 . C. 10. D. 9 .
Câu 18. [ Mức độ 4]Cho hàm số bậc ba y f x có đồ thị như hình vẽ:
 Gọi S là tập hợp tất cả các giá trị nguyên của tham số m để hàm số y f x2 2x m có 3 
 điểm cực trị. Tổng các phần tử của S là: 
 A. 6 . B. 9 .C. 10. D. 5 .
Câu 19. [ Mức độ 3] Cho hàm số y f x là hàm số bậc bốn có đồ thị như hình vẽ dưới đây. Tổng số 
 x 3 x 3
 đường tiệm cận ngang và tiệm cận đứng của đồ thị hàm số y g x là 
 2 f 2 x f x 
 A. 5 . B. 6 . C. 7 . D. 8 .
Câu 20. [ Mức độ 3] Cho hàm số f x ax3 bx2 cx d có đồ thị như hình vẽ 
 Trang 5 ĐỀ THI THỬ TRƯỜNG X TỈNH Y LẦN Z-2020 
 x2 2x 3
 Hỏi đồ thị hàm số g x có bao nhiêu đường tiệm cận?
 f 2 x 4 f x 
 A. 2 . B. 3 . C. 5 . D. 6 .
Câu 21. [Mức độ 3]Cho hàm số f (x) ax3 bx2 cx d,a 0 có đồ thị như hình vẽ dưới đây. 
 Có bao nhiêu giá trị nguyên của tham số m để đồ thị hàm số 
 x4 x2 2020
 g x có đúng 6 đường tiệm cận.
 f 2 x 2 m 1 . f x 5 2m 3 
 A. 5. B. 1. C. .3 D. . 0
Câu 22. [ Mức độ 3] Cho hàm số f x ax3 bx2 cx d a,b,c,d R có đồ thị như hình vẽ. Đồ 
 x3 7x2 15x 9
 thị hàm số g x 2 có bao nhiêu đường tiệm cận đứng?
 f x 2 f x 
 A. 4 .B. 2 . C. 6 .D. 3 .
Câu 23. [ Mức độ 3] Cho hàm số y f x có đồ thị như vẽ. Số đường tiệm cận của đồ thị hàm số
 2 f x 
 y là: 
 f 2 x 2 f x 
 Trang 6 ĐỀ THI THỬ TRƯỜNG X TỈNH Y LẦN Z-2020 
 y
 2
 1
 1 O x
 2
 A. 5 . B. 3 . C. 4 . D. 6 .
Câu 24. [MỨC ĐỘ 3] Cho hàm số y f x có đồ thị như hình vẽ. Hỏi tổng số đường tiệm cận đứng và 
 2021x
 tiệm cận ngang của đồ thị hàm số g x ?
 f x f x 1 
 A. 5 . B. 6 . C. 7 . D. 8 .
Câu 25. [Mức độ 3] Cho y f x là hàm số bậc ba, xác định và liên tục trên ¡ .
 2020
 Đồ thị hàm số g x có nhiều nhất bao nhiêu đường tiệm cận?
 f x3 2x 1
 A. 4. B. 2. C. 5. D. 3.
Câu 26. [ Mức độ 4] Cho hàm số y f (x) x2 4x 3 có đồ thị như hình vẽ
 Tổng số đường tiệm cận đứng và tiệm cận ngang của đồ thị hàm số
 Trang 7 ĐỀ THI THỬ TRƯỜNG X TỈNH Y LẦN Z-2020 
 x2 2022x 2040 2x2 x
 y là
 x f 2 ( x ) f ( x ) 
 A. 12. B. 10 C. 8 D. 13.
Câu 27. [ Mức độ 4] Cho hàm số y f x có đạo hàm liên tục trên ¡ . Đồ thị y f x như hình vẽ. 
 x2 1
 Số đường tiệm cận đứng của đồ thị hàm số y là 
 f 2 x 4 f x 
 A. 1 B. 2 C. 3 D. 4.
Câu 28. [ Mức độ 3] Cho hàm số y f x xác định và liên tục trên đoạn  2;6 , có bảng biến thiên 
 như hình vẽ dưới đây
 Gọi M ,m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số 
 y f sin x 3 cos x 2 . Tính giá trị của biểu thức M m .
 A. 2 . B. 1. C. 6 . D. 7 .
Câu 29. [ Mức độ 3] Cho đa thức f x thỏa mãn 2 f x f x 1 x2 x ¡ với Gọi M ,m lần 
 lượt là GTLN, GTNN của f x trên tập D  2;1. Tính giá trị của biểu thức 
 S 27 M m 2020 
 A. 2041.B. 2042.C. 2043.D. 2044.
 23 
Câu 30. [ Mức độ 3] Cho hai hàm số y f (x) và y g(x) liên tục trên khoảng 3; lần lượt có đồ 
 2 
 thị và có bảng biến thiên như hình vẽ. Biết giá trị cực đại và giá trị cực tiểu của hàm số 
 y f (x) lần lượt là 2 và 2 . Gọi m và M lần lượt là giá trị nhỏ nhất và giá trị lớn nhất của 
 23 
 hàm số y g( f (x)) trên khoảng 3; . Khảng định nào sau đây đúng?
 2 
 Trang 8 ĐỀ THI THỬ TRƯỜNG X TỈNH Y LẦN Z-2020 
 13
 x
 3 2 0 1 2 2
 g'(x) + 0 0 + 0 0 +
 2021 2020 2022
 g(x)
 2019
 2017 2018
 A. m 2017 và M 2022 . B. m 2 và M 2 .
 C. m 2018 và M 2021.D. m 2018 và không tồn tại M .
Câu 31. [ Mức độ 3] Cho hàm số y f x liên tục trên ¡ đồng thời thỏa mãn điều kiện f 0 0 và 
 4 2 2
 f x 6x f x 9x 3x 4,x ¡ . Tìm giá trị lớn nhất của hàm số y f 2x 3x 1 
 trên đoạn 0;1.
 5 167 17 155
 A. . B. . C. . D. .
 2 69 7 64
Câu 32. [ Mức độ 4] Cho hàm số y f x có đồ thị như hình vẽ bên dưới. Khi 
 2 1 3 2 9 1 3 2 9 
 g x 2 f x 3x x 1 8 f x 3x x 1 đạt giá trị nhỏ nhất bằng a thì 
 2 2 2 2 
 1 3 2 9 
 phương trình f x 3x x 1 a có bao nhiêu nghiệm thực?
 2 2 
 A y
 2
 1
 -2 -1 O 1 2 x
 B
 Trang 9 ĐỀ THI THỬ TRƯỜNG X TỈNH Y LẦN Z-2020 
 A. 5. B. Vô số. C. 4. D. 6.
Câu 33. [Mức độ 3] Cho hàm số y = f (x) liên tục trên đoạn [- 1;3] và có bảng biến thiên như sau
 Gọi M , m lần lượt là giá trị lớn nhất, giá trị nhỏ nhất của hàm số 
 g(x)= f ((2cos x + 1)(cos x- 3sin x)- 1 - 1). Giá trị của 3M + 2m bằng
 A. 25 . B. 5 . C. 0 . D. 25 .
Câu 34. [ Mức độ 3] Cho hàm số f x x4 2x2 . Gọi S là tập hợp tất cả các giá trị thực của tham số 
 m sao cho giá trị lớn nhất của hàm số y f cos x 1 m đạt giá trị nhỏ nhất. Tổng các phần 
 tử của S bằng
 7
 A. 4 .B. 7 . C. m . D. 6 .
 2
 1
Câu 35. [ Mức độ 3] Tính tích tất cả các số thực m để hàm số y x4 x2 3x m có giá trị nhỏ 
 4
 nhất trên đoạn [- 2; 2] bằng 6 là.
 A. 432 . B. - 216 . C. - 155 . D. 288 .
Câu 36. [ Mức độ 4] Cho hàm số y f x có đạo hàm trên ¡ và có đồ thị như hình vẽ. Đặt hàm số 
 y g(x) f 2x3 x 1 m.. Tìm m để max g(x) 10 .
 0;1
 A. m 13 . B. m 3 . C. m 12 . D. m 1.
Câu 37. [ Mức độ 4] Cho hàm số y f x có bảng biến thiên như sau:
 Trang 10