Đề ôn tập kiểm tra đợt 9 môn Toán Lớp 12 - Tổ 20 - Chủ đề: Ứng dụng tích phân - Năm học 2020-2021 (Có đáp án)

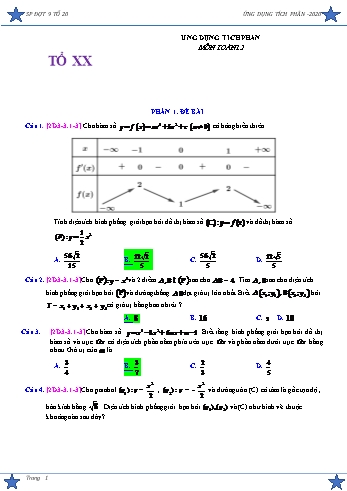
 SP ĐỢT 9 TỔ 20 ỨNG DỤNG TÍCH PHÂN -2020 
 ỨNG DỤNG TÍCH PHÂN
 MÔN TOÁN12
 TỔ XX
 PHẦN 1. ĐỀ BÀI
 Câu 1. [2D3-3.1-3] Cho hàm số y f x ax4 bx2 c a 0 có bảng biến thiên
 Tính diện tích hình phẳng giới hạn bởi đồ thị hàm số (C) : y f (x) và đồ thị hàm số 
 1
 (P) : y x2 .
 2
 56 2 12 2 56 2 12 5
 A. . B. . C. . D. .
 15 5 5 5
 Câu 2. [2D3-3.1-3] Cho (P): y = x2 và 2 điểm A,B Î (P) sao cho AB = 4 . Tìm A,B sao cho diện tích 
 hình phẳng giới hạn bởi (P) và đường thẳng AB đạt giá trị lớn nhất. Biết A(x1 ; y1 ),B(x2 ; y2 ) hỏi 
 T = x1 + y1 + x2 + y2 có giá trị bằng bao nhiêu ?
 A. 8 . B. .1 6 C. . D.2 . 10
Câu 3. [2D3-3.1-3] Cho hàm số y x3 3x2 6mx m 1 . Biết rằng hình phẳng giới hạn bởi đồ thị 
 hàm số và trục cóOx diện tích phần nằm phía trên trục vàO phầnx nằm dưới trục bằngOx 
 nhau. Giá trị của mlà
 3 3 2 4
 A. . B. . C. . D. .
 4 7 3 5
 x 2 x 2
 Câu 4. [2D3-3.1-3] Cho parabol (p ) : y = , (p ) : y = - và đường tròn (C) có tâm là gốc tọa độ , 
 1 2 2 2
 bán kính bằng 8 . Diện tích hình phẳng giới hạn bởi (p1),(p2) và (C) như hình vẽ thuộc 
 khoảng nào sau đây?
 Trang 1 SP ĐỢT 9 TỔ 20 ỨNG DỤNG TÍCH PHÂN -2020 
 A. (14;16). B. (8;10). C. .( 10;12) D. (12;14)
Câu 5. [2D3-3.2-3] Cắt một tấm bìa hình tròn có đường kính AB bằng 10 cm. Vẽ 1 Parabol đi qua A, 
 B và sao cho đỉnh Parabol cách mép tấm bìa 1 khoảng 1cm, rồi lấy đối xứng qua AB. Sau đó 
 dùng kéo cắt bỏ phần bìa giới hạn bởi hai Parabol. Diện tích phần bìa còn lại gần đúng với giá 
 trị nào sau đây?
 A. 21,16. B. 19.
 C. 30,256. D. 25,206 .
Câu 6. [2D3-3.1-3] Một vật chuyển động trong 3 giờ với vận tốc v Km / h phụ thuộc thời gian t h có 
 đồ thị là một phần của đường Parabol như hình bên. 
 Tính quãng đường S mà vật di chuyển được trong 3 giờ đó. 
 A. 6 Km . B. 5 Km C. .2 0 Km D. . 2 Km
Câu 7. [2D3-3.1-3] Cho hai hàm số f x x 4 bx2 c và g x dx2 ex f có đồ thị như hình bên. 
 Trang 2 SP ĐỢT 9 TỔ 20 ỨNG DỤNG TÍCH PHÂN -2020 
 Tính diện tích hình phẳng giới hạn bởi hai đồ thị. 
 64 128
 A. . B. 4 C. . D. .8
 15 15
 x2 x 2
Câu 8. [2D3-3.1-3] Cho hàm số f x có đồ thị là C như hình bên, 
 x 2
 gọi d là tiếp tuyến của C tại điểm A 1;0 . Tính diện tích hình phẳng giới hạn bởi C , ,d 
 đường thẳng y x 3 và đường thẳng x 2 . 
 A. .S 4ln 2B. .2 C. S 4ln 2 2 S 8ln 2 2 . D. S 8ln 2 2 .
Câu 9. [2D3-3.1-4] Cho hàm số y f x xác định và liên tục trên ¡ . Đồ thị của hàm số y f ' x 
 như hình bên dưới. 
 Trang 3 SP ĐỢT 9 TỔ 20 ỨNG DỤNG TÍCH PHÂN -2020 
 x2
 Đặt g x f x x . Mệnh đề nào dưới đây đúng:
 2
 A. g 2 g 3 g 0 . B. g 0 g 2 g 3 .
 C. g 2 g 0 g 3 . D. .g 3 g 0 g 2 
 Câu 10. [2D3-2.2-3] Trong mặt phẳng tọa độ Oxy , cho H là hình phẳng giới hạn bởi hai parabol 
 2 2
 P1 : y x 2x 3 và P2 : y x 2mx m , trong đó m là tham số thực và m 3;7 . 
 Gọi S là diện tích của H . Giá trị lớn nhất của S là
 85184 44 8 88 11
 A. . B. . C. . D. .
 3 3 3 3
 Câu 11. [2D3-3.1-3] Diện tích hình phẳng giới hạn bởi các đường: y x2 4 ; y x 2
 31 44
 A. 18 . B. . C. . D. . 17
 3 3
Câu 12. [2D3-3.1-4] Cho hàm số y x 4 2x 2 có đồ thị C , đường thẳng y m 2cắt đồ thị Ctại hai 
 điểm phân biệt A ,B . Gọi H là hình phẳng giới hạn bởi đồ thị C và hai tia OA ,OB . Tìm 
 m sao cho diện tích hình H bằng diện tích OAB với O là gốc tọa độ.
 40 40 40 10
 A. . B. . C. . D. .
 9 3 3 3
 Câu 13. [2D3-3.2-3] Một khu vườn hình bán nguyệt có bán kính R 4m , ở giữa khu vườn người ta 
 3
 muốn tạo một cái bể cá dạng parabol có phương trình y x2 3(như hình vẽ), phần còn 
 4
 lại sẽ trồng hoa. Biết chi phí xây bể cá là 400000đồng /m2, chi phí trồng hoa là 200000đồng 
 /m2 . Chi phí xây dựng khu vườn gần giá trị nhất là 
 A. 6đồng.24084 1 B. 6220485 đồng. C. 6240184 đồng. D. 6250184 đồng.
 Trang 4 SP ĐỢT 9 TỔ 20 ỨNG DỤNG TÍCH PHÂN -2020 
Câu 14. [2D3-3.5-3] Một nhà máy nhiệt điện sử dụng 90 máng Parabol thu nhiệt năng lượng mặt trời có 
 cùng kích thước, bề mặt cong đều nhau (tham khảo hình vẽ). Mỗi máng có chiều rộng 2m , bề dày 
 của khối silic làm mặt máng là 2dm , chiều dài 3m . Đặt máng tiếp giáp mặt đất có điểm cao nhất 
 của khối silic làm mặt máng so với mặt đất là 5dm . Khi đó thể tích (tính theo đơn vị m3 ) của khối 
 silic làm 90 mặt máng là 
 A. 10 m3 . B. 108 m3 . C. .1 20m3 D. . 30 m3
Câu 15. [2D3-3.2-3] Trường ĐHBK Hà Nội có cổng là hình dáng của một parabol có khoảng cách 2 chân 
 cổng là 10m, chiều cao cổng là 12,5m. Để chuẩn bị trang trí cổng chào mừng năm mới, nhà 
 trường muốn làm cánh cửa cổng hình chữ nhật có 2 đỉnh nằm trên parabol còn 2 đỉnh dưới mặt 
 đất như hình vẽ, phần diện tích không làm cánh cổng nhà trường dùng để trang trí hoa (tham 
 khảo hình vẽ). Biết chi phí để trang trí 1m2 hoa là 300.000 đồng. Nhà trường mua hoa với chi 
 phí thấp nhất gần đúng với giá trị nào sau đây? 
 A. 11.200.000. B. 10.560.000. C. .1 0.600.00D.0 . 12.000.000
Câu 16. [2D3-3.1-3] Cho hàm số y x2 4x 3 có đồ thị là parabol P và điểm M 3;2 . Gọi d là 
 đường thẳng đi qua điểm M và S là diện tích hình phẳng được giới hạn bởi đường thẳng d 
 Trang 5 SP ĐỢT 9 TỔ 20 ỨNG DỤNG TÍCH PHÂN -2020 
 a 2 a 3 3
 và parabol P , khi đó Smin với a,b ¢ và tối giản. Giá trị biểu thức 2a 3b 
 b b
 bằng
 A. 1105 . B. 1051 . C. 1240 . D. 59878 .
 4 2
Câu 17. [2D3-3.1-3] Cho hàm số y x mx có đồ thị Cm với m 0 . Giả sử Cm cắt trục Ox tại 
 ba điểm phân biệt như hình vẽ. Gọi S1 và S2 là diện tích các miền tô đậm được cho trên hình 
 16 2
 vẽ. Tìm m để S S .
 1 2 15
 A. .m 1 B. m 2 . C. m 2 . D. .m 4
Câu 18. [2D3-3.5-2] Một cái ly làm bằng thủy tinh , có hình dạng là khối nón cụt và các kích thướt như 
 hình vẽ. 
 Phần rỗng bên trong có thiết diện qua trục là Parabol .
Thể tích khối thủy tinh bằng bao nhiêu?
 65 33 43 55
 A. B. C. D. 
 4 4 4 4
Câu 19. [2D3-3.1-3] Cho hình phẳng S giới hạn bởi đồ thị y f x ,y g x và trục hoành như 
 hình vẽ .
 Trang 6 SP ĐỢT 9 TỔ 20 ỨNG DỤNG TÍCH PHÂN -2020 
 a 
 Thể tích khối tròn xoay tạo thành khi quay hình phẳng S xung quanh trục Ox có dạng V 
 b
 a
 (với là phân số tối giảng). Kết quả log a 3b bằng ?
 b 2
 A. 14 B. 5 C. 32 D. 11 
 2
Câu 20. [2D3-3.1-3] Cho Parabol P : y x 4x có đỉnh I và A là giao điểm khác O của 
 P với trục hoành. M là điểm bất kì trên cung IA , tiếp tuyến của P tại M cắt Ox,Oy lần 
 lượt tại B,C . Gọi S1, S2 lần lượt là diện tích của hai tam giác cong MAB, MOC . Tìm M sao 
 cho S1 S2 nhỏ nhất.
 8 32 8 160 
 A. .M 4;0 B. M 3;3 . C. M ; . D. . M ; 
 3 9 3 9 
Câu 21. [2D3-3.1-3] Cho hàm số y f x có đạo hàm liên tục trên ¡ và f 0 2 . Hàm số 
 y f x có đồ thị như hình vẽ bên.
 Biết rằng diện tích hình phẳng giới hạn bởi trục Ox và đồ thị hàm số y f x trên đoạn
  1; 0 và 0 ; 2 lần lượt bằng 3 và .7Giá trị của biểu thức f 1 f 2 bằng 
 A. .2 B. 1. C. 6 . D. .5
Câu 22. [2D3-3.1-3] Gọi d là đường thẳng đi qua điểm A 0; 1 và có hệ số góc bằng k k 0 ; H 
 là hình phẳng giới hạn bởi đồ thị hàm số y 2x3 1và đường thẳng d Tìm. kđể diện tích 
 hình phẳng H bằng 4.
 3
 A. k 3. B. k 4 . C. .k 6 D. . k 
 2
 Trang 7 SP ĐỢT 9 TỔ 20 ỨNG DỤNG TÍCH PHÂN -2020 
Câu 23. [2D3-3.1-3] Cho hàm số y f (x) ax3 bx2 cx d a,b,c,d ¡ ,a 0 có đồ thị C đi 
 qua gốc tọa độ và đồ thị hàm số y f '(x) cho bởi hình vẽ bên. Diện tích S của hình phẳng 
 giới hạn bới đồ thị hàm số y f x , trục hoành và các đường thẳng x 1, x 1 là
 5 1
 A. . B. . C. . 1 D. . 0
 2 2
 2
Câu 24. [2D3-3.3-3] Cho hình phẳng D giới hạn bởi các đường y x và đường thẳng x 4 . Thể tích 
 của khối tròn xoay sinh ra khi D xoay quanh trục Ox là:
 A. 8 . B. .V 4 C. . V D.6 . V 10 
Câu 25. [2D3-3.5-3] Một ô tô bắt đầu chuyển động nhanh dần đều với vận tốc v1 t 5t 4 (m / s) . Đi 
 được 6 (s) người lái xe phát hiện chướng ngại vật và phanh gấp, ô tô tiếp tục chuyển động 
 chậm dần đều với gia tốc a 34 (m / s2 ) . Tính quãng đường S (m) đi được của ô tô từ lúc 
 bắt đầu chuyển bánh cho đến khi dừng hẳn.
 A. S 131(m). B. S 114(m). C. S 150,5(m). D. S 17(m).
Câu 26. [2D3-3.3-3] Thể tích khối tròn xoay bị giới hạn bởi đồ thị các hàm số f x : y x2 6x 6 , 
 1
 g x : y x2 2x 2 , h x : y x2 2x 2 , x 4 , x 4 và trục Ox (như hình bên) là:
 2
 Trang 8 SP ĐỢT 9 TỔ 20 ỨNG DỤNG TÍCH PHÂN -2020 
 56224 848 64 
 A. V . B. V 64 . C. .V D. . V 
 15 15 3
Câu 27. [2D3-3.1-3] Cho hàm số y f x x 2 4x có đồ thị C và đường thẳng d đi qua điểm 
 M 2;1 . Khi đó, hình phẳng giới hạn bởi C và d có diện tích nhỏ nhất bằng: 
 10 5 20 5 10 5 20 5
 A. . B. . C. . D. .
 9 3 3 9
Câu 28. [2D3-3.3-3] Trong mặt phẳng tọa độ Oxy , cho hình thang ABCD với A 3,0 , B 3,3 , 
 C 4,6 , D 4,0 . Quay hình thang ABCD quanh trục Ox thì thể tích khối tròn xoay tạo thành 
 là bao nhiêu.
 63 
 A. .5 9 B. . C. 215 . D. 147 .
 2
Câu 29. [2D3-3.1-3] Cho parabol P : y 2x2 và đường thẳng d cắt P tại hai điểm phân biệt 
 A, B sao cho AB 3 . Diện tích hình phẳng giới hạn bởi P và đường thẳng d có giá trị lớn 
 nhất bằng
 A. .2 7 B. . 18 C. 6 . D. 9 .
 2 2
Câu 30. [2D3-3.1-3] Cho đường tròn C : x 1 y 1 4 ; Từ A(1;3) kẻ được 2 tiếp tuyến 
 (d1),(d2 ) tới đường tròn; Diện tích hình phẳng được giới hạn bởi đường tròn (C) và hai tiếp 
 tuyến (d1),(d2 ) là ? 
 4 2 
 A. S 4 3 . B. .S 2 3 
 3 3
 2 2 
 C. .S 2 3 D. . S 4 3 
 3 3
Câu 31. [2D3-3.1-3] Cho P : y x2 và d : y mx 1. Có bao nhiêu giá trị của mđể hình phẳng giới 
 4
 hạn bởi d và P có diện tích bằng .
 3
 A. 0 . B. 1. C. .2 D. . 4
 Trang 9 SP ĐỢT 9 TỔ 20 ỨNG DỤNG TÍCH PHÂN -2020 
Câu 32. [2D3-3.5-3] Một người thợ bơm nước vào bể chứa nước. Gọi h t là thể tích nước bơm được 
 sau t giờ. Cho h t 6at 2 2bt và ban đầu bể không có nước. Sau 3 giờ thì thể tích nước trong 
 bể là 90m3 , sau 6 giờ thì thể tích nước trong bể là 504m3 . Tính thể tích nước trong bể sau khi 
 bơm được 12 giờ.
 A. .9 00m3 B. . 1200mC.3 2360 m3. D. 3168 m3 .
Câu 33. [2D3-5.5-3] Hình phẳng H giới hạn bởi parabol y 2x 2và đường cong có phương trình 
 y 1 x2 . Diện tích của hình phẳng H bằng:
 1 1 1 1
 A. . B. . C. . D. .
 4 2 4 6 6 6 4 6
 2020x 1
Câu 34. [2D3-3.1-3] Cho hàm số y f x và y g x 4040x 1 . Đặt 
 2020x 1
 h x 2.20202 x 2021 f g x và k x h x dx 20202 x2 2018x với h 0 0 . Diện 
 tích hình phẳng giới hạn bởi các đường y k x , y x2 , x 2, x 1 bằng 
 11 1 1 3
 A. . B. . C. . D. .
 6 2 2020 2020
Câu 35. [2D3-3.2-3] Một tấm kim loại hình Elip có độ dài trục lớn bằng 80cm và độ dài trục bé bằng 
 60cm . Hai đường Parabol P1 và P2 đi qua tâm và các đỉnh của hình chữ nhật cơ sở của 
 Elip, đồng thời P1 và P2 đối xứng nhau qua trục lớn phân chia Elip thành hai phần (như 
 hình vẽ). Phần tô màu người ta mạ Đồng, phần còn lại người ta mạ Bạc. Giá mạ đồng là 100 
 ngàn đồng/ dm2 và giá mạ bạc là 200 ngàn đồng/ dm2 . Hỏi số tiền để mạ tấm kim loại trên gần 
 với số nào nhất trong các số sau?
 A. 6,33 triệu đồng. B. 5,72 triệu đồng. C. 6,68 triệu đồng. D. 4,16 triệu đồng.
Câu 36. [2D3-3.4-3] Một viên thuốc của trẻ em có dạng khối tròn xoay với chiều cao là 2c m(tham 
 khảo hình vẽ). Khi cắt viên thuốc theo một mặt phẳng vuông góc với trục của nó thì ta luôn 
 1
 được thiết diện là một hình tròn có bán kính R cm với x 0;2 là khoảng cách từ 
 x 1
 mặt cắt tới mặt đáy lớn của viên thuốc ( tính theo đơn vị cm ). Tìm độ dài k cm là khoảng 
 cách giữa đáy lớn với mặt cắt để ta đánh dấu vị trí có thể cắt đôi viên thuốc (theo phương 
 vuông góc với trục) thành hai phần có thể tích như nhau? 
 A. .1 cm B. . 0.8 C.cm 0,75 cm . D. 0,5 cm .
 Trang 10