Đề kiểm tra học kì II môn Toán Lớp 12 (Dành cho học sinh khá giỏi) - Năm học 2020-2021 (Có đáp án)

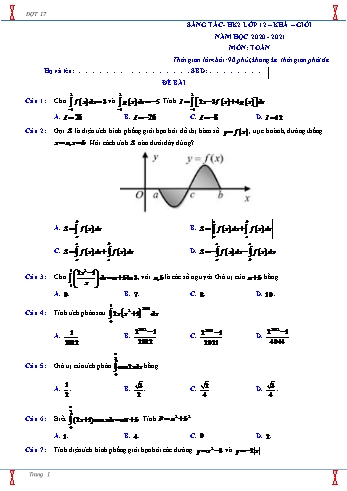
 ĐỢT 17
 SÁNG TÁC- HK2 LỚP 12 – KHÁ – GIỎI 
 NĂM HỌC 2020 - 2021
 MÔN: TOÁN 
 Thời gian làm bài: 90 phút, không kể thời gian phát đề
 Họ và tên: .. SBD: .
 ĐỀ BÀI 
 2 2 2
Câu 1: Cho f x dx 3 và g x dx 5 . Tính I 2x 3 f x 4g x dx .
 1 1 1
 A. I 26 . B. I 26 . C. I 8 . D. I 12 .
Câu 2: Gọi S là diện tích hình phẳng giới hạn bởi đồ thị hàm số y f x , trục hoành, đường thẳng 
 x a, x b . Hỏi cách tính S nào dưới đây đúng?
 b c b
 A. S f x dx . B. S f x dx f x dx .
 a a c
 c b c c
 C. S f x dx f x dx . D. S f x dx f x dx .
 a c a b
 3 2x2 1 
Câu 3: Cho dx a bln 3 , với a,b là các số nguyên. Giá trị của a b bằng
 1 x 
 A. 9 . B. 7 . C. 8 . D. 10 .
 1
 2021
Câu 4: Tính tích phân sau 2x x2 1 dx
 0
 1 22022 1 22021 1 22022 1
 A. . B. . C. . D. .
 2022 2022 2021 4044
 6
Câu 5: Giá trị của tích phân cos 2xdx bằng
 0
 1 3 2 3
 A. . B. . C. . D. .
 2 2 4 4
 2
Câu 6: Biết (2x 1)cos xdx a b . Tính P a 2 b 2
 0
 A. 1. B. 4 . C. 0 . D. 2 .
Câu 7: Tính diện tích hình phẳng giới hạn bởi các đường y x2 3 và y 2 x
 Trang 1 ĐỢT 17
 12 10 5 10
 A. B. C. D. 
 3 3 3 6
Câu 8: Tính thể tích của khối tròn xoay khi quay hình phẳng giới hạn bởi các đường y x3 4x, y 0 , 
 x 1, x 1 quanh trục Ox.
 407 814 2048 477 
 A. . B. . C. . D. .
 105 105 105 105
 3 1
Câu 9: Cho I f x dx 2020 . Tính tích phân J f 2x 1 dx .
 1 0
 A. 2021. B. 4040 . C. 1010. D. 2020 .
 1
Câu 10: Tích phân x 2 e2xdx a be2 , với a,b là các số hữu tỉ. Biểu thức a b bằng:
 0
 1 1
 A. 2 B. C. D. 2
 2 2
 3
Câu 11: Biết I x ln x2 1 dx a ln10 bln 2 c trong đó a , b , c là các số nguyên. Tính giá trị của 
 1
 biểu thức T a b c .
 A. T 5 . B. T 2 . C. T 0 . D. T 10 .
 1 2
Câu 12: Cho f là hàm số liên tục thỏa f x dx 2021. Tính I cos x. f sin x dx .
 0 0
 A. 2020. B. 2019. C. 2022. D. 2021.
 b
 b 1 e 1
Câu 13: Biết dx 2 , trong đó a,b là các số thực dương. Tính tích phân dx .
 a x ea x ln x
 1 1
 A. I ln 2 . B. I 2 . C. I . D. I .
 ln 2 2
 3 3x2 5x 1
Câu 14: Cho tích phân I dx a ln 2 bln 3 c . Với a ,b , c ¤ . Tính giá trị của biểu thức 
 2
 1 x x
 T 3a2 3a c
 A. 1. B. 0 . C. 1. D. 2 .
 2 2
Câu 15: Cho số phức z thỏa mãn: z 1 2i 1 2i . Tính mođun của số phức w iz 4
 A. w 5 . B. 2 5 . C. 2 . D. 5 .
Câu 16:. Cho số phức z thỏa mãn điều kiện: 1 2i z z i . Tìm số phức z .
 1 1 1 1
 A. z 1 2i . B. z i . C. z 2 i . D. z i .
 2 2 2 2
Câu 17: . Cho số phức z thỏa mãn điều kiện: 1 i z z 2 i . Tìm module của số phức
 w 2z 3i .
 A. w 2 19 . B. w 19 . C. w 2 29 . D. w 29 .
Câu 18: Tìm số phức liên hợp z của số phức z (3 2i)(2 3i).
 Trang 2 ĐỢT 17
 A. z 5i. B. z 6 6i. C. z 12 5i D. z 6 6i.
Câu 19: Tìm các số thực x, y biết 2x 3y 1 x 2y i 3x 2y 2 4x y 3 i
 9 4 9 4 9 4 9 4
 A. x , y B. x , y C. x , y D. x , y 
 11 11 11 11 11 11 11 11
Câu 20: Cho số phức z thoả mãn hệ thức z 3 i 5 . Tập hợp các điểm biểu diễn của z là một đường 
 tròn có bán kính là
 A. R 3 . B. R 1. C. R 5 D. R 9 .
Câu 21: Cho số phức z thoả mãn hệ thức z 3 (1 i) 2i . Phẩn ảo của số phức z bằng
 A. 3 . B. 1. C. 5 . D. 9 .
Câu 22: Biết nghịch đảo của số phức z bằng số phức liên hợp của nó. Khi đó:
 A. z 1. B. z 2. C. z là số thực. D. z là số thuần ảo.
 2
Câu 23: Gọi z1 và z2 là hai nghiệm phức của phương trình z 6z 12 0 . Tính giá trị của biểu thức 
 P z1 z2
 A. P 4 3 B. P 2 3 C. P 6 D. P 3
Câu 24: Cho số phức z thỏa mãn 3z iz 15 13i. Tìm môđun của z.
 A. 5. B. 25. C. 5. D. 7.
Câu 25: Trong mặt phẳng phức, cho 3 điểm A, B, C lần lượt là điểm biểu diễn của các số phức 
 z1 1 i, z2 1 3i, z3 . Biết tam giác ABC vuông cân tại A và z3 có phần thực dương. Khi 
 đó, tọa độ điểm C là:
 A. 2 ; 2 . B. 3 ; 3 . C. 8 1;1 . D. 1; 1 .
Câu 26: Trong không gian Oxyz , góc giữa hai vectơ j và u 0; 3 ;1 là
 A. 1200 . B. 600 . C. 1500 . D. 300 .
Câu 27: Trong không gian với hệ tọa độ Oxyz , viết phương trình mặt phẳng P đi qua điểm M 1;2;3 
 x 1 y 7 z 3
 và vuông góc với đường thẳng : .
 2 1 4
 A. 2x y 4z 16 0. B. 2x y 4z 16 0 .
 C. 2x y 4z 16 0 . D. 2x y 4z 16 0.
Câu 28: Trong không gian với hệ tọa độ Oxyz , cho mặt phẳng P : x y 2z 3 0 và điểm I 1;1;0 . 
 Phương trình mặt cầu tâm I và tiếp xúc với P là
 2 2 5 2 2 25
 A. x 1 y 1 z2 . B. x 1 y 1 z2 .
 6 6
 2 2 5 2 2 25
 C. x 1 y 1 z2 . D. x 1 y 1 z2 .
 6 6
 x 1 y 2 z 3
Câu 29: Trong không gian Oxyz , cho đường thẳng d : và điểm A 1; 4; 5 . Viết 
 2 3 1
 phương trình mặt phẳng P đi qua A song song đường thẳng d và trục Ox .
 Trang 3 ĐỢT 17
 A. y 3z 19 0 B. y 3z 19 0 . C. y 3z 19 0 . D. y 3z 19 0 .
Câu 30: Trong không gian với hệ tọa độ Oxyz , cho mặt phẳng P : x y z 3 0 . Điểm M 1;2; 3 
 có hình chiếu lên P là điểm M a;b;c . Tổng a b c bằng bao nhiêu?
 A. 3. B. 3 . C. 0 . D. 6 .
Câu 31: Trong không gian Oxyz , cho mặt phẳng P : 2x y z 4 0 và mặt phẳng 
 Q : x 3y 2z 2 0 . Đường thẳng d là giao tuyến của mặt phẳng P và mặt phẳng Q 
 có phương trình là
 x 1 y 1 z 3 x 1 y 1 z 3
 A. . B. .
 1 5 7 1 5 7
 x 1 y 1 z 3 x 1 y 1 z 3
 C. . D. .
 1 5 7 1 5 7
.
Câu 32: Trong không gian Oxyz , cho điểm A 1;0;4 và đường thẳng d có phương trình 
 x 1 y z 1
 . Tìm phương trình đường thẳng đi qua A , vuông góc và cắt d .
 1 1 2
 x 1 y z 2 x 1 y z 2 x 1 y z 2 x 1 y z 4
 A. . B. . C. . D. .
 2 2 1 1 3 1 1 1 1 1 1 1
 x 2 y 1 z 5
Câu 33: Trong không gian Oxyz , cho đường thẳng : và mặt phẳng 
 3 4 5
 :3x 4y 5z 2021 0 . Góc giữa và bằng
 A. 30 . B. 60 . C. 0 . D. 90 .
Câu 34: Trong không gian Oxyz , cho tam giác ABC có A 2; 3;1 , B 4;1; 2 , C 6; 3; 7 . Diện tích 
 tam giác ABC bằng
 A. 14. B. 24 . C. 8 . D. 24 .
Câu 35: Trong không gian Oxyz , cho 4 điểm A 6; –2;3 , B 0;1;6 , C 2;0; –1 , D 4;1;0 . Tính thể 
 tích tứ diện ABCD .
 A. VABCD 96 . B. VABCD 24 . C. VABCD 72 . D. VABCD 12.
 2 x5 3x ex5 3x a 1 b.e 
Câu 36: Biết I dx ln 1 , với a,b là hai số nguyên dương. Tính 
 x 
 0 e.3 3 eln 3 e 
 T a b2 .
 A. 84 . B. 41. C. 96 . D. 25 .
Câu 37: Hình phẳng được tô đậm trong hình dưới đây được giới hạn bởi đường tròn, đường parabol, trục 
 hoành và có diện tích S a 2 b c , với a,b,c ¤ . Tính tổng 3a 3b 2c .
 Trang 4 ĐỢT 17
 y
 2
 1
 I
 O 1 2 x
 A. 5 . B. 7 . C. 9 . D. 11.
Câu 38: Một vật chuyển động trong 3 giờ với vận tốc v km / h phụ thuộc vào thời gian t h có đồ thị 
 hàm số là một phần của parabol có đỉnh B 2;6 và trục đối xứng song song với trục tung như 
 hình vẽ. Tính quãng đường S mà vật di chuyển được trong 3 giờ đó.
 A. 15 km . B. 33 km . C. 16 km . D. 30 km .
Câu 39: Cho hàm số y f x có đạo hàm trên ¡ , hàm số y f x là hàm bậc hai có đồ thị như hình 
 11 9
 vẽ dưới và có diện tích S , S .
 1 6 2 2
 Mệnh đề nào sau đây đúng ?
 æ5ö
 A. f (0)< f (1)< f (4).B. f ç ÷< f (4)< f (1).
 èç2ø÷
 æ5ö æ5ö
 C. f ç ÷< f (0)< f (1). D. f (1)< f (4)< f ç ÷.
 èç2ø÷ èç2ø÷
Câu 40: Trên tập hợp số phức, cho phương trình z2 bz c 0 với b,c ¡ . Biết rằng hai nghiệm của 
 phương trình có dạng 2w 1 3i và iw 2 3i , với w là một số phức. Tính giá trị của biểu 
 thức S 2b2 c .
 A. 294 . B. 409 . C. 27 . D. 37 .
Câu 41: Cho số phức z thỏa mãn z 2 z 3i là một số thuần ảo. Tập hợp điểm biểu diễn số phức z 
 là một đường tròn có chu vi bằng.
 13 13 
 A. 13 . B. 2 13 . C. . D. .
 2 4
Câu 42: Cho số phức z thỏa mãn hệ thức z 2 3i z i . Giá trị nhỏ nhất của biểu thức 
 Trang 5 ĐỢT 17
 P 2z i 1 2i bằng
 7 2 7 7 2 7 3
 A. . B. . C. . D. .
 2 2 3 3
Câu 43: Trong không gian với hệ tọa độ Oxyz , cho hai điểm A 1;0;0 , B 0;0;2 và mặt cầu 
 S : x2 y2 z2 2x 2y 1 0 . Số mặt phẳng chứa hai điểm A , B và tiếp xúc với mặt cầu 
 S là
 A. 1 mặt phẳng. B. 2 mặt phẳng. C. 0 mặt phẳng. D. Vô số mặt phẳng.
Câu 44: Trong không gian Oxyz cho ba điểm A 1;1; 0 , B 3; 1; 2 , C 1; 6; 7 . Tìm tọa độ điểm M 
 2 2 2
 trên mặt phẳng Oxz sao cho MA MB MC nhỏ nhất.
 A. M 3; 0; 1 . B. M 1; 0; 0 . C. M 1; 0; 3 . D. M 1;1; 3 .
 x y z x 1 y z 1
Câu 45: Trong không gian với hệ tọa độ Oxyz , cho hai đường thẳng d : ; d : 
 1 1 2 2 1 1 
 và mặt phẳng P : x y z 0. Phương trình nào sau đây là phương trình của đường thẳng 
 song song với P , cắt d và d lần lượt tại M và N mà MN 2.
 7x 4 7y 4 7z 8 7x 4 7y 4 7z 8
 A. : . B. : .
 3 8 5 3 8 5
 7x 1 7y 4 7z 3 7x 1 7y 4 7z 8
 C. : . D. : .
 3 8 5 3 8 5
Câu 46: Cho hàm số y f x có đạo hàm liên tục trên ¡ và thỏa mãn điều kiện: 
 1
 6 3 4 37
 x . f x 64. f x 1 0, x ¡ và f 1 . Tính tích phân f x dx .
 64 0
 229 229 256 256
 A. . B. . C. . D. .
 256 256 229 229
Câu 47: Cho hàm số y f x ax3 2x2 bx 1 và y g x cx2 4x d có đồ thị như hình vẽ. Biết 
 đồ thị hàm số y f x và y g x cắt nhau tại ba điểm phân biệt x1, x2 , x3 thỏa mãn 
 x1 x2 x3 9. Tính diện tích hình phẳng S giới hạn bởi đồ thị hàm số y f x và đường 
 thẳng y 1.
 9 27
 A. S . B. . C. 3 . D. 9 .
 4 4
 Trang 6 ĐỢT 17
Câu 48: Cho số phức z thỏa mãn z 3 7i 2 và biểu thức P z 2 2 z 2i 2 đạt giá trị lớn nhất. 
 Giá trị z 2 2i bằng
 A. 58 . B. 41 . C. 38 . D. 61 .
 8 4 8 
Câu 49: Trong không gian Oxyz cho điểm A 2,2,1 và điểm B ; ; . Gọi là đường phân giác 
 3 3 3 
 trong của góc A của tam giác OAB . Điểm M a;b;c trên sao cho MO OB đạt giá trị nhỏ 
 nhất. Hỏi T 7a 8b 2021c có giá trị bằng
 A. 2019 . B. 2020 . C. 2017 . D. 2018 .
Câu 50: Trong không gian với hệ trục toạ độ Oxyz , gọi d là đường thẳng đi qua điểm M 2; 1;1 , song 
 song với mặt phẳng P : x 2y z 2021 0 sao cho tổng khoảng cách từ các điểm 
 A 2; 2;0 , B 1;0;3 tới đường thẳng đó đạt giá trị nhỏ nhất. Vectơ chỉ phương của d là 
  
 2 2 2
 ud a;b;c . Tổng a b c bằng:
 A. 2020 . B. 30 . C. 100. D. 120.
 BẢNG ĐÁP ÁN
 1.B 2.D 3.B 4.B 5.D 6.D 7.B 8.B 9.C 10.B
 11.C 12.D 13.B 14.B 15.B 16.D 17.D 18.C 19.A 20.C
 21.B 22.A 23.A 24.A 25.D 26.C 27.A 28.B 29.B 30.A
 31.C 32.D 33.D 34.A 35.D 36.C 37.A 38.A 39.C 40.A
 41.A 42.A 43.A 44.C 45.B 46.A 47.A 48.A 49.D 50.D
 HƯỚNG DẪN GIẢI
 2 2 2
Câu 1: [Mức độ 2] Cho f x dx 3 và g x dx 5 . Tính I 2x 3 f x 4g x dx .
 1 1 1
 A. I 26 . B. I 26 . C. I 8 . D. I 12 .
 Lời giải
 Trang 7 ĐỢT 17
 Fb, tác giả: Nguyễn Hoàng Tuyên
 2
 Ta có: I 2x 3 f x 4g x dx
 1
 2 2
 2
 x2 3 f x dx 4 g x dx
 1 
 1 1
 (4 1) 3.3 4 5 26 .
Câu 2: [Mức độ 2] Gọi S là diện tích hình phẳng giới hạn bởi đồ thị hàm số y f x , trục hoành, 
 đường thẳng x a, x b (như hình vẽ bên). Hỏi cách tính S nào dưới đây đúng?
 b c b
 A. S f x dx . B. S f x dx f x dx .
 a a c
 c b c c
 C. S f x dx f x dx . D. S f x dx f x dx .
 a c a b
 Lời giải
 Tác giả: Trần Quang Đạt; Fb: Quang Đạt
 b c b c b
 Ta có: S f x dx f x dx f x dx f x dx f x dx
 a a c a c
 c c
 f x dx f x dx
 a b
 3 2x2 1 
Câu 3: [Mức độ 2] Cho dx a bln 3 , với a,b là các số nguyên. Giá trị của a b bằng
 1 x 
 A. 9 . B. 7 . C. 8 . D. 10 .
 Lời giải
 FBTác giả: Van mai
 3 2 3
 2x 1 1 3
 dx 2x dx x2 ln x 8 ln 3 a 8,b 1 a b 7
 1
 1 x 1 x 
 1
 2021
Câu 4: [Mức độ 2] Tính tích phân sau 2x x2 1 dx
 0
 1 22022 1 22021 1 22022 1
 A. . B. . C. . D. .
 2022 2022 2021 4044
 Lời giải
 FBTác giả: Van mai
 Trang 8 ĐỢT 17
 Đặt t x 2 1 2xdx dt ; Đổi cận x 0 t 1; x 1 t 2
 1 2 2022 2 2022
 2021 t 2 1
 Khi đó: 2x x2 1 dx t 2021dt .
 0 1 2022 1 2022
 6
Câu 5: [Mức độ 2] Giá trị của tích phân cos 2xdx bằng
 0
 1 3 2 3
 A. . B. . C. . D. .
 2 2 4 4
 Lời giải
 Tác giả: Trần Quang Đạt; Fb: Quang Đạt
 6 1 1 3
 Ta có cos 2xdx sin 2 x 6 (sin sin 0) 
 0 2 0 2 3 4
 2
Câu 6: [Mức độ 2] Biết (2x 1)cos xdx a b . Tính P a 2 b 2
 0
 A. 1. B. 4 . C. 0 . D. 2 .
 Lời giải
 Tác giả: Trần Quang Đạt; Fb: Quang Đạt
 u 2x 1 du 2dx
 Đặt 
 dv cos xdx v sin x
 2 2 
 Ta có: (2x 1)cos xdx (2x 1)sin x 2 2sin xdx 1 2cos x 2
 0 0 0 0
 1 2(cos cos0) 1. Vậy P a2 b2 12 ( 1)2 2 .
 2
Câu 7: [Mức độ 2] Tính diện tích hình phẳng giới hạn bởi các đường y x2 3 và y 2 x
 12 10 5 10
 A. B. C. D. 
 3 3 3 6
 Lời giải
 FB tác giả: Thông Đình Đình
 2
 Phương trình hoành độ giao điểm x2 3 2 x x 2 x 3 0 x 1 x 1.
 1 0 1
 Diện tích hình phẳng là: S x2 3 2 x dx x2 3 2x dx x2 3 2x dx
 1 1 0
 Mà x2 3 2x 0 x 1;0 và x2 3 2x 0 x 0;1 nên
 0 1
 S x2 3 2x dx x2 3 2x dx
 1 0
 0 1
 3 3
 x 2 x 2 5 5 10
 3x x 3x x .
 3 3 3 3 3
 1 0
 Trang 9 ĐỢT 17
Câu 8: [Mức độ 2] Tính thể tích của khối tròn xoay khi quay hình phẳng giới hạn bởi các đường 
 y x3 4x, y 0 , x 1, x 1 quanh trục Ox.
 407 814 2048 477 
 A. . B. . C. . D. .
 105 105 105 105
 Lời giải
 FB tác giả: Thông Đình Đình
 1
 2 814 
 V π x3 4x dx .
 1 105
 3 1
Câu 9: [Mức độ 2] Cho I f x dx 2020 . Tính tích phân J f 2x 1 dx .
 1 0
 A. 2021. B. 4040 . C. 1010. D. 2020 .
 Lời giải
 FB tác giả: Thông Đình Đình
 dt
 Đặt t 2x 1 dt 2dx dx . Đổi cận: x 0 t 1; x 1 t 3 .
 2
 3
 1 1 1 1
 Khi đó J f 2x 1 dx f t dt I .2020 1010 .
 0 2 1 2 2
 1
Câu 10: [Mức độ 2] Tích phân x 2 e2xdx a be2 , với a,b là các số hữu tỉ. Biểu thức a b bằng:
 0
 1 1
 A. 2 B. C. D. 2
 2 2
 Lời giải
 Fb, Tác giả: Trần Mạnh Sang
 du dx
 u x 2 1 1 1 1 1
 Đặt . Suy ra: x 2 e2xdx x 2 e2x e2xdx
 2x 1 2x 
 dv e dx v e 0 2 0 0 2
 2
 1 1 1 1 1 1 3 5 5 3e2
 e2 1 e2x e2 1 e2 e2 .
 2 4 0 2 4 4 4 4 4
 5 3 1
 Suy ra a ,b , suy ra a b .
 4 4 2
 3
Câu 11: [Mức độ 2] Biết I x ln x2 1 dx a ln10 bln 2 c trong đó a , b , c là các số nguyên. 
 1
 Tính giá trị của biểu thức T a b c .
 A. T 5 . B. T 2 . C. T 0 . D. T 10 .
 Lời giải
 Fb, tác giả: Trần Mạnh Sang
 2x
 2 du dx
 u ln x 1 x2 1
 Đặt , ta có .
 x2 1
 dv xdx v 
 2
 Trang 10