Đề kiểm tra 45 phút môn Hình học Lớp 11 - Đề số 1 - Chủ đề: Kiểm tra phép vị tự, phép đồng dạng - Năm học 2020-2021 (Có đáp án)

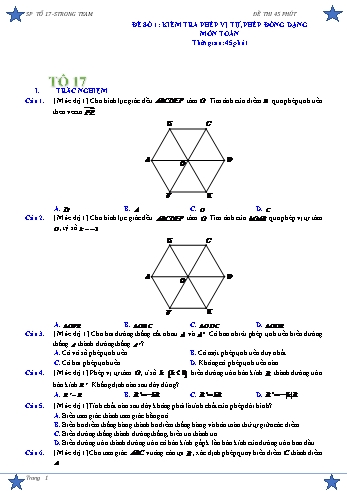
 SP TỔ 17-STRONG TEAM ĐỀ THI 45 PHÚT 
 ĐỀ SỐ 1: KIỂM TRA PHÉP VỊ TỰ, PHÉP ĐỒNG DẠNG
 MÔN TOÁN
 Thời gian: 45 phút
 TỔ 17
 I. TRẮC NGHIỆM
Câu 1. [ Mức độ 1] Cho hình lục giác đều ABCDEF tâm O . Tìm ảnh của điểm B qua phép tịnh tiến 
  
 theo vecto FE .
 B C
 A D
 O
 F E
 A. D . B. A . C. O . D. C .
Câu 2. [ Mức độ 1] Cho hình lục giác đều ABCDEF tâm O . Tìm ảnh của OAB qua phép vị tự tâm 
 O , tỷ số k 1.
 B C
 A D
 O
 F E
 A. OFE . B. OBC . C. ODC . D. ODE .
Câu 3. [ Mức độ 1] Cho hai đường thẳng cắt nhau d và d ' . Có bao nhiêu phép tịnh tiến biến đường 
 thẳng d thành đường thẳng d ' ? 
 A. Có vô số phép tịnh tiến. B. Có một phép tịnh tiến duy nhất.
 C. Có hai phép tịnh tiến. D. Không có phép tịnh tiến nào.
Câu 4. [ Mức độ 1] Phép vị tự tâm O , tỉ số k k 0 biến đường tròn bán kính R thành đường tròn 
 bán kính R ' . Khẳng định nào sau đây đúng?
 A. R ' R . B. R ' kR . C. R ' kR . D. R ' k R .
Câu 5. [ Mức độ 1] Tính chất nào sau đây không phải là tính chất của phép dời hình?
 A. Biến tam giác thành tam giác bằng nó.
 B. Biến ba điểm thẳng hàng thành ba điểm thẳng hàng và bảo toàn thứ tự giữa các điểm.
 C. Biến đường thẳng thành đường thẳng, biến tia thành tia.
 D. Biến đường tròn thành đường tròn có bán kính gấp k lần bán kính của đường tròn ban đầu.
Câu 6. [ Mức độ 1] Cho tam giác ABC vuông cân tại B , xác định phép quay biến điểm C thành điểm 
 A .
 Trang 1 SP TỔ 17-STRONG TEAM ĐỀ THI 45 PHÚT 
 Q C A Q A C Q A C Q C A
 A. B, 90 . B. B,90 . C. B, 90 . D. B,90 .
Câu 7. [ Mức độ 1] Hình gồm hai đường tròn không đồng tâm và có bán kính khác nhau có bao nhiêu 
 trục đối xứng?
 A. Vô số. B. 3. C. 2. D. 1.
Câu 8. [ Mức độ 2] Trong hệ tọa độ Oxy , tìm phương trình đường tròn C là ảnh của đường tròn 
 C :x2 y2 1 qua phép đối xứng tâm I 1; 0 .
 A. x2 y2 1. B. x2 y 2 2 1.
 C. x 1 2 y2 1. D. x 2 2 y2 1.
Câu 9. [ Mức độ 2] Trong mặt phẳng tọa độ Oxy , tìm phương trình đường thẳng là ảnh của đường 
 thẳng : x 2y 0 qua phép tịnh tiến theo véctơ v 1;1 .
 A. : x 2y 3 0 . B. : x 2y 1 0 . C. : x 2y 1 0 . D. : x 2y 2 0.
Câu 10. [ Mức độ 2] Trong mặt phẳng tọa độ Oxy , cho A 3;2 , B 1;1 . Gọi A x1; y1 , B x2 ; y2 
 lần lượt là ảnh của A , B qua phép vị tự tâm O , tỉ số k 2 . Tính S x1x2 y1 y2.
 A. 2 . B. 2 . C. 4 . D. 4 .
Câu 11. [Mức độ 2] Trong mặt phẳng Oxy , cho đường thẳng d :5x 3y 15 0 . Xác định phương 
 trình đường thẳng d là ảnh của đường thẳng d qua phép quay tâm O , góc quay 90 .
 A. 3x 5y 15 0 . B. 5x 3y 15 0 .
 C. 3x 5y 15 0. D. 3x 5y 15 0 .
Câu 12. [Mức độ 2] Trong mặt phẳng Oxy , cho đường tròn C : x2 y2 2x 10y 1 0 và đường 
 tròn C ' : x 3 2 y 1 2 25. Phép đối xứng trục qua đường thẳng nào sau đây biến đường 
 tròn C thành đường tròn C ' .
 A. d : x 2y 0. B. d : 2x y 4 0.
 C. d : x 2y 4 0. D. d : x 2y 4 0.
Câu 13. Trong hệ tọa độ Oxy , tìm phép tịnh tiến vecto v biến điểm A(1;4) thành điểm B( 1;3) ?
 A. v 2 ;1 . B. v 2 ; 1 . C. v 2 ;1 . D. v 2 ; 1 .
 2 2
Câu 14. Trong hệ tọa độ Oxy , cho đường tròn (C) có phương trình x 3 y 2 25 và đường 
 2
 tròn (C ') có phương trình x 7 y2 225 . Phép vị tự tâm A(1; 3) tỉ số k biến (C) thành 
 (C ') Tìm k?
 A. k 2 . B. k 3. C. k 5 .D. k 6 .
Câu 15. [ Mức độ 3] Trong mặt phẳng tọa độ Oxy , cho tam giác ABC có A 1; 1 , B 0 ; 3 và 
 C 4 ; 4 . Tam giác A B C là ảnh của tam giác ABC qua phép đồng dạng bằng cách thực 
 Trang 2 SP TỔ 17-STRONG TEAM ĐỀ THI 45 PHÚT 
 hiện liên tiếp phép tịnh tiến u 1;1 và phép vị tự tâm O tỷ số k 2 . Tính diện tích tam giác 
 A B C . 
 A. 15. B. 8 17 . C. 20 2 . D. 30 .
 II.TỰ LUẬN
Câu 16. [ Mức độ 2] Trong mặt phẳng tọa độ Oxy , cho đường thẳng d : 2x 3y 9 0 . Tìm phương 
 trình đường thẳng d là ảnh của d qua phép đối xứng tâm O .
Câu 17. [ Mức độ 3] Cho tam giác ABC có trực tâm H. Gọi M1, M2, M3 lần lượt là trung điểm của BC, 
 CA, AB; H1, H2, H3 lần lượt là chân đường cao hạ từ các đỉnh A, B, C và A1, B1, C1 lần lượt là 
 trung điểm của HA, HB, HC. Chứng minh rằng 9 điểm M1, M2, M3, H1, H2, H3, A1, B1, C1 cùng 
 nằm trên một đường tròn.
Câu 18. [ Mức độ 4] Trong mặt mẳng tọa độ Oxy cho điểm A 1;2 , tìm B Ox ,C d : y x sao 
 cho chu vi tam giác ABC nhỏ nhất.
 Trang 3 SP TỔ 17-STRONG TEAM ĐỀ THI 45 PHÚT 
 HƯỚNG DẪN GIẢI
Câu 1. [ Mức độ 1] Cho hình lục giác đều ABCDEF tâm O . Tìm ảnh của điểm B qua phép tịnh tiến 
  
 theo vecto FE .
 B C
 A D
 O
 F E
 A. D . B. A . C. O . D. C .
 Lời giải
 FB tác giả: Phùng Nguyễn 
   
 Từ vì ABCDEF là hình lục giác đều nên suy ra BC FE .
  
 Vậy TFE B C .
Câu 2. [ Mức độ 1] Cho hình lục giác đều ABCDEF tâm O . Tìm ảnh của OAB qua phép vị tự tâm 
 O , tỷ số k 1.
 B C
 A D
 O
 F E
 A. OFE . B. OBC . C. ODC . D. ODE .
 Lời giải
 FB tác giả: Phùng Nguyễn 
 Từ hình vẽ 
 V O, 1 O O , V O, 1 A D , V O, 1 B E
 Vậy V O, 1 OAB ODE .
Câu 3. [ Mức độ 1] Cho hai đường thẳng cắt nhau d và d ' . Có bao nhiêu phép tịnh tiến biến đường 
 thẳng d thành đường thẳng d ' ? 
 A. Có vô số phép tịnh tiến. B. Có một phép tịnh tiến duy nhất.
 C. Có hai phép tịnh tiến. D. Không có phép tịnh tiến nào.
 Lời giải
 FB tác giả: Đào Dương 
 Phép tịnh tiến biến một đường thẳng thành một đường thẳng song song hoặc trùng với đường 
 thẳng đã cho. Mà d và d ' là hai đường thẳng cắt nhau nên không có phép tịnh tiến nào biến 
 d thành d ' .
 Trang 4 SP TỔ 17-STRONG TEAM ĐỀ THI 45 PHÚT 
Câu 4. [ Mức độ 1] Phép vị tự tâm O , tỉ số k k 0 biến đường tròn bán kính R thành đường tròn 
 bán kính R ' . Khẳng định nào sau đây đúng?
 A. R ' R . B. R ' kR . C. R ' kR . D. R ' k R .
 Lời giải
 FB tác giả: Đào Dương 
 Phép vị tự tỉ số k biến đường tròn bán kính R thành đường tròn bán kính R ' k R . Mà 
 k 0 nên R ' kR .
Câu 5. [ Mức độ 1] Tính chất nào sau đây không phải là tính chất của phép dời hình?
 A. Biến tam giác thành tam giác bằng nó.
 B. Biến ba điểm thẳng hàng thành ba điểm thẳng hàng và bảo toàn thứ tự giữa các điểm.
 C. Biến đường thẳng thành đường thẳng, biến tia thành tia.
 D. Biến đường tròn thành đường tròn có bán kính gấp k lần bán kính của đường tròn ban đầu.
 Lời giải
 FB tác giả: Lê Hoàng Hạc 
 Phép dời hình biến đường tròn thành đường tròn có cùng bán kính chọn D .
Câu 6. [ Mức độ 1] Cho tam giác ABC vuông cân tại B , xác định phép quay biến điểm C thành điểm 
 A .
 A. Q B, 90 C A . B. Q B,90 A C . C. Q B, 90 A C . D. Q B,90 C A.
 Lời giải
 FB tác giả: Lê Hoàng Hạc 
 Phép quay tâm B biến điểm C thành điểm A là Q B,90 C A.
Câu 7. [ Mức độ 1] Hình gồm hai đường tròn không đồng tâm và có bán kính khác nhau có bao nhiêu 
 trục đối xứng?
 A. Vô số. B. 3. C. 2. D. 1.
 Lời giải
 FB tác giả: Lê Hoàng Khâm 
 Có 1 trục đối xứng là đường thẳng đi qua tâm của hai đường tròn.
 Iסּ d 
 I
Câu 8. [ Mức độ 2] Trong hệ tọa độ Oxy , tìm phương trình đường tròn C là ảnh của đường tròn 
 C :x2 y2 1 qua phép đối xứng tâm I 1; 0 .
 A. x2 y2 1. B. x2 y 2 2 1.
 Trang 5 SP TỔ 17-STRONG TEAM ĐỀ THI 45 PHÚT 
 C. x 1 2 y2 1. D. x 2 2 y2 1.
 Lời giải
 FB tác giả: Lê Hoàng Khâm 
 Đường tròn C có tâm O 0; 0 , bán kính R 1.
 Gọi O là ảnh của O qua phép đối xứng tâm I 1; 0 nên I là trung điểm OO .
 xO xO 
 xI
 2 xO 2xI xO xO 2.1 0
 Ta có: O 2; 0 .
 y y y 2y y y 2.0 0
 O O y O I O O 
 2 I
 Đường tròn C là ảnh của đường tròn C qua phép đối xứng tâm I 1; 0 .
 C có tâm O 2; 0 , bán kính R R 1.
 Phương trình đường tròn C là: x 2 2 y2 1.
Câu 9. [ Mức độ 2] Trong mặt phẳng tọa độ Oxy , tìm phương trình đường thẳng là ảnh của đường 
 thẳng : x 2y 0 qua phép tịnh tiến theo véctơ v 1;1 .
 A. : x 2y 3 0 . B. : x 2y 1 0 . C. : x 2y 1 0 . D. : x 2y 2 0.
 Lời giải
 FB tác giả: Nguyễn Văn Trường Giang
 x x 1 x x 1
 Xét ; .
 M x; y Tv M M x ; y M x 1; y 1 
 y y 1 y y 1
 Do M x; y nên x 1 2 y 1 0 x 2y 1 0.
 Lại có: .
 Tv M x ; y 
 Vậy phương trình đường thẳng là ảnh của đường thẳng có dạng: x 2y 1 0 .
Câu 10. [ Mức độ 2] Trong mặt phẳng tọa độ Oxy , cho A 3;2 , B 1;1 . Gọi A x1; y1 , B x2 ; y2 
 lần lượt là ảnh của A , B qua phép vị tự tâm O , tỉ số k 2 . Tính S x1x2 y1 y2.
 A. 2 . B. 2 . C. 4 . D. 4 .
 Lời giải
 FB tác giả: Nguyễn Văn Trường Giang
   x 2x 6
 1 A
 Ta có: V O;2 A A OA 2OA .
 y1 2yA 4
   x 2x 2
 2 B
 Ta có: V O;2 B B OB 2OB .
 y2 2yB 2
 Vậy S x1x2 y1 y2 6.2 4.2 4 .
Câu 11. [Mức độ 2] Trong mặt phẳng Oxy , cho đường thẳng d :5x 3y 15 0 . Xác định phương 
 trình đường thẳng d là ảnh của đường thẳng d qua phép quay tâm O , góc quay 90 .
 A. 3x 5y 15 0 . B. 5x 3y 15 0 .
 C. 3x 5y 15 0. D. 3x 5y 15 0 .
 Trang 6 SP TỔ 17-STRONG TEAM ĐỀ THI 45 PHÚT 
 Lời giải
 FB tác giả: Võ Đức Toàn
 Cách 1:
 Do Q O ; 90 d d nên d '  d . Do đó d ' có phương trình dạng: 3x 5y m 0 .
 Chọn M 3;0 d , gọi M ' x '; y ' d ' là ảnh của điểm M qua phép quay Q o ; 90 
 x ' yM 0
 Suy ra: M ' 0; 3 .
 y ' xM 3
 Do M 0; 3 d nên 3.0 5. 3 m 0 m 15.
 Vậy d có phương trình là 3x 5y 15 0 .
 Cách 2:
 Với mọi điểm M x; y d, M ' x '; y ' d ' sao cho Q O ; 90 M M '. 
 x ' y x y '
 Khi đó ta có: . 
 y ' x y x '
 Do M x; y d nên ta có 5x 3y 15 0 5y ' 3x ' 15 0 3x ' 5y ' 15 0.
 Do M ' x '; y ' d ' nên d ' có phương trình là 3x 5y 15 0 . 
Câu 12. [Mức độ 2] Trong mặt phẳng Oxy , cho đường tròn C : x2 y2 2x 10y 1 0 và đường 
 tròn C ' : x 3 2 y 1 2 25. Phép đối xứng trục qua đường thẳng nào sau đây biến đường 
 tròn C thành đường tròn C ' .
 A. d : x 2y 0. B. d : 2x y 4 0.
 C. d : x 2y 4 0. D. d : x 2y 4 0.
 Lời giải
 FB tác giả: Võ Đức Toàn 
 Đường tròn C có tâm A 1;5 và bán kính R 5.
 Đường tròn C ' có tâm B 3;1 và bán kính R 5.
 Khi đó trục cần tìm chính là đường trung trực của đoạn AB .
 Gọi M 2;3 là trung điểm của AB . 
   
 Ta có AB 2; 4 . Đường trung trực của đoạn AB qua M 2;3 nhận AB 2; 4 làm vtpt 
 có phương trình: 2 x 2 4 y 3 0 hay x 2y 4 0.
Câu 13. Trong hệ tọa độ Oxy , tìm phép tịnh tiến vecto v biến điểm A(1;4) thành điểm B( 1;3) ?
 A. v 2 ;1 . B. v 2 ; 1 . C. v 2 ;1 . D. v 2 ; 1 .
 Lời giải
 FB tác giả: Hung Duong 
  
 Phép tịnh tiến theo vecto v biến A thành B v AB 2 ; 1 
 Trang 7 SP TỔ 17-STRONG TEAM ĐỀ THI 45 PHÚT 
 2 2
Câu 14. Trong hệ tọa độ Oxy , cho đường tròn (C) có phương trình x 3 y 2 25 và đường 
 2
 tròn (C ') có phương trình x 7 y2 225 . Phép vị tự tâm A(1; 3) tỉ số k biến (C) thành 
 (C ') Tìm k?
 A. k 2 . B. k 3. C. k 5 .D. k 6 .
 Lời giải
 Đường tròn (C) có tâm I 3 ; 2 , bán kính R 5
 Đường tròn (C ') có tâm I ' 7 ; 0 , bán kính R ' 15
 Phép vị tự tâm A tỉ số k biến (C) thành (C ')
   
 AI ' k AI (6 ; 3) k(2 ; 1) k 3 .
Câu 15. [ Mức độ 3] Trong mặt phẳng tọa độ Oxy , cho tam giác ABC có A 1; 1 , B 0 ; 3 và 
 C 4 ; 4 . Tam giác A B C là ảnh của tam giác ABC qua phép đồng dạng bằng cách thực 
 hiện liên tiếp phép tịnh tiến u 1;1 và phép vị tự tâm O tỷ số k 2 . Tính diện tích tam giác 
 A B C . 
 A. 15. B. 8 17 . C. 20 2 . D. 30 .
 Lời giải
 FB tác giả: Nguyễn Thanh Sang 
 Tính được: AB 17 , AC 5 2 và BC 17 .
 15
 Khi đó: S p p AB p BC p AC 
 ABC 2
 Ta thấy tam giác ABC và tam giác A B C đồng dạng với nhau theo tỉ số đồng dạng là 2. 
 15
 Nên S 4. 30 .
 A'B'C ' 2
Câu 16. [ Mức độ 2] Trong mặt phẳng tọa độ Oxy , cho đường thẳng d : 2x 3y 9 0 . Tìm phương 
 trình đường thẳng d là ảnh của d qua phép đối xứng tâm O .
 Lời giải
 FB tác giả: Nguyễn Thanh Sang 
 Gọi M x ; y d và M x ; y d 
 x x x x 
 Qua phép đối xứng tâm O ta có: .
 y y y y 
 Suy ra : d : 2 x 3 y 9 0 hay d : 2x 3y 9 0 .
 Vậy d có phương trình là 2x 3y 9 0 .
Câu 17. Cho tam giác ABC có trực tâm H. Gọi M1, M2, M3 lần lượt là trung điểm của BC, CA, AB; H1, 
 H2, H3 lần lượt là chân đường cao hạ từ các đỉnh A, B, C và A1, B1, C1 lần lượt là trung điểm 
 của HA, HB, HC. Chứng minh rằng 9 điểm M1, M2, M3, H1, H2, H3, A1, B1, C1 cùng nằm trên 
 một đường tròn.
 Lời giải
 Trang 8 SP TỔ 17-STRONG TEAM ĐỀ THI 45 PHÚT 
 A
 M'2
 M'3
 H'
 A1 2
 M2
 M
 3 H
 H'3 2
 H3
 H C1
 B1
 M
 B H1 1 C
 H'1 M'1
 + Gọi M'1, M'2, M'3 lần lượt là điểm đối xứng của H qua M1, M2, M3
 H'1, H'2, H'3 lần lượt là điểm đối xứng của H qua BC, CA, AB
 + Ta có ĐBC biến tam giác HBC thành tam giác H'1BC nên BH '1 C BHC , mà 
 0 0
 BHC H2HH3,H2HH3 BAC 180 do đó BH '1 H BAC 180 , suy 
 ra tứ giác ABH'1C nội tiếp một đường tròn, suy ra H'1 nằm trên đường tròn ngoại tiếp tam giác 
 ABC.
 + Chứng minh tương tự ta có H'2, H'3 nằm trên đường tròn ngoại tiếp tam giác ABC.
 + Ta có Đ biến tam giác BHC thành tam giác BM'1C nên nên BM ' C BHC , mà 
 M1 1
 0 0
 BHC H2HH3,H2HH3 BAC 180 nên BM '1 H BAC 180 , suy 
 ra tứ giác ABM'1C nội tiếp một đường tròn, suy ra M'1 nằm trên đường tròn ngoại tiếp tam giác 
 ABC.
 + Chứng minh tương tự ta có M'2, M'3 nằm trên đường tròn ngoại tiếp tam giác ABC.
 + Ta có biến các điểm A, B, C, M' , M' , M' , H' , H' , H' lần lượt thành các điểm A , 
 V 1 1 2 3 1 2 3 1
 H ; 
 2 
 B1, C1, M1, M2, M3, H1, H2, H3. Mà các điểm A, B, C, M'1, M'2, M'3, H'1, H'2, H'3 cùng nằm trên 
 đường tròn ngoại tiếp tam giác ABC nên các điểm A1, B1, C1, M1, M2, M3, H1, H2, H3 cùng 
 nằm trên một đường tròn.
Câu 18. [ Mức độ 4] Trong mặt mẳng tọa độ Oxy cho điểm A 1;2 , tìm B Ox ,C d : y x sao 
 cho chu vi tam giác ABC nhỏ nhất.
 Lời giải
 FB tác giả: Nguyễn Vĩnh Thái 
 Trang 9 SP TỔ 17-STRONG TEAM ĐỀ THI 45 PHÚT 
 Gọi M và L lần lượt là điểm đối xứng của A qua Ox và d khi đó M 2; 1 , và L 1;2 .
 B Ox , ta có BA BM ,C d , ta có CA CL . 
 AB BC CA MB BC CL MC .
 x 2 1 5
 Do đó chu vi tam giác ABC nhỏ nhất khi B x;0 Ox  ML x 
 1 3 3
 a 2 a 1 5
 và C a;a d  ML a 
 1 3 4
 5 5 5 
 Vậy B ;0 , C ; .
 3 4 4 
Trang 10