Đề kiểm tra 45 phút môn Giải tích Lớp 11 - Chương IV - Năm học 2020-2021 (Có đáp án)

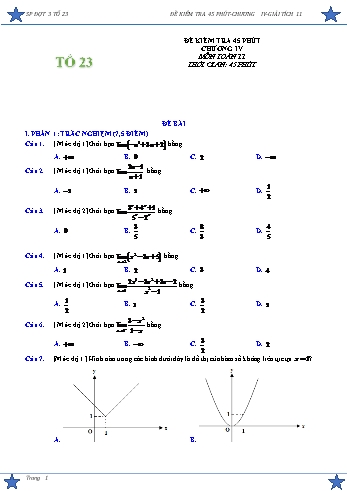
 SP ĐỢT 3 TỔ 23ĐỀ KIỂM TRA 45 PHÚT-CHƯƠNG IV-GIẢI TÍCH 11
 ĐỀ KIỂM TRA 45 PHÚT
 CHƯƠNG IV
 MÔN TOÁN 11
 TỔ 23 THỜI GIAN: 45 PHÚT
 ĐỀ BÀI
I. PHẦN 1: TRẮC NGHIỆM (7,5 ĐIỂM)
Câu 1. [ Mức độ 1] Giới hạn lim n3 3n 2 bằng
 A. . B. 0 . C. 2 . D. .
 2n 1
Câu 2. [ Mức độ 1] Giới hạn lim bằng
 n 1
 1
 A. 2 . B. 2 . C. . D. .
 2
 3n 4n 1
Câu 3. [ Mức độ 2] Giới hạn lim bằng
 5n 2n
 3 8 4
 A. 0 . B. . C. . D. .
 5 3 5
Câu 4. [ Mức độ 1] Giới hạn lim x2 3x 5 bằng
 x 2 
 A. 1. B. 2 . C. 3 . D. 4 .
 2x3 3x2 3x 2
Câu 5. [ Mức độ 1] Giới hạn lim bằng
 x 1 x2 1
 1 3
 A. . B. 1. C. . D. 2 .
 2 2
 3 x2
Câu 6. [ Mức độ 2] Giới hạn lim bằng
 x 1 1 x
 3
 A. . B. . C. . D. 2 .
 2
Câu 7. [Mức độ 1 ] Hình nào trong các hình dưới đây là đồ thị của hàm số không liên tục tại x 1? 
 A. B. 
 Trang 1 SP ĐỢT 3 TỔ 23ĐỀ KIỂM TRA 45 PHÚT-CHƯƠNG IV-GIẢI TÍCH 11
 C. D. 
Câu 8. [ Mức độ 1] Hàm số nào sau đây gián đoạn tại x 2 ?
 3x 4
 A. y x3 1. B. y x4 2x2 1. C. y sin x . D. y .
 x 2
 x2 7x 12
 khi x 3
Câu 9. [Mức độ 2] Cho hàm số y x 3 . Tìm giá trị của tham số m để hàm số 
 2m 1 khi x 3
 liên tục tại điểm x 3.
 A. m 1. B. m 2 . C. m 0 D. m 1.
Câu 10. [ Mức độ 1] Hàm số nào dưới đây liên tục trên khoảng ; ?
 1 2x 1
 A. y x . B. y 2 x . C. y . D. y x 7 .
 x x 7
 x2 x khi x 1
Câu 11. [ Mức độ 2] Tìm m để hàm số f (x) 2 khi x 1 liên tục trên tập xác định của nó.
 mx 1 khi x 1
 A. m 2 . B. m 3 . C. m 4 . D. m 1.
 2x2 2x
 khi x 1
Câu 12. [ Mức độ 2] Tìm m để hàm số f (x) x 1 liên tục trên tập xác định của nó.
 5m khi x 1
 1 1 2
 A. m 1. B. m . C. m 4 , m . D. m .
 2 2 5
 x 2 2
Câu 13. [ Mức độ 2] Giới hạn lim bằng
 x 2 x 2
 1 1
 A. . B. .C. 0 . D. 1.
 2 4
 x2 4x 3
 , x 1
Câu 14. [ Mức độ 3] Với giá trị nào của tham số m thì hàm số f x 1 x2 có giới hạn tại 
 2x m, x 1
 x 1.
 A. m 3 . B. m 1. C. m 0 . D. m 1.
 x 4 2
 , x 0
 x
Câu 15. [ Mức độ 3] Có bao nhiêu giá trị của tham số m để hàm số f x có giới 
 1
 mx m2 , x 0
 4
 hạn tại x 0 .
 A. 0 . B. 2 . C. 1. D. 3 .
 Trang 2 SP ĐỢT 3 TỔ 23ĐỀ KIỂM TRA 45 PHÚT-CHƯƠNG IV-GIẢI TÍCH 11
II. PHẦN 2: TỰ LUẬN (2,5 ĐIỂM)
 4x 1 1
 khi x 0
Câu 16. [ Mức độ 2] Tìm các giá trị của tham số a để hàm số f (x) ax2 (2a 1)x liên 
 3 khi x=0
 tục tại x 0.
 1 1 1 
Câu 17. [ Mức độ 3] Tính lim ... .
 1.3 2.4 n. n 2 
 ax2 (a 2)x 2
 khi x 1
Câu 18. [ Mức độ 3] Cho hàm số f (x) x 3 2 . Tìm các giá trị nguyên của a để 
 2
 8 a khi x=1
 hàm số liên tục tại x 1.
 Trang 3 SP ĐỢT 3 TỔ 23ĐỀ KIỂM TRA 45 PHÚT-CHƯƠNG IV-GIẢI TÍCH 11
 BẢNG ĐÁP ÁN
 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15
 D B A C C B D D A D D D B B C
 ĐÁP ÁN CHI TIẾT
I. PHẦN 1: TRẮC NGHIỆM (7,5 ĐIỂM)
Câu 1. [ Mức độ 1] Giới hạn lim n3 3n 2 bằng
 A. . B. 0 . C. 2 . D. .
 Lời giải
 FB tác giả: Trần Văn Thiết 
 3 3 3 3 2 
 Ta có: lim n 3n 2 lim n 3n 2 lim n . 1 2 3 .
 n n 
 3 3 2 
 lim n ,lim 1 2 3 1 0.
 n n 
 Vậy lim n3 3n 2 .
 2n 1
Câu 2. [ Mức độ 1] Giới hạn lim bằng
 n 1
 1
 A. 2 . B. 2 . C. . D. .
 2
 Lời giải
 FB tác giả: Trần Văn Thiết 
 1
 2 
 2n 1 2
 Ta có: lim lim n 2.
 1
 n 1 1 1
 n
 3n 4n 1
Câu 3. [ Mức độ 2] Giới hạn lim bằng
 5n 2n
 3 8 4
 A. 0 . B. . C. . D. .
 5 3 5
 Lời giải
 FB tác giả: Trần Văn Thiết
 n n n
 3 4 1 
 n n 
 3 4 1 5 5 5 0
 Ta có: lim n n lim n 0.
 5 2 2 1
 1 
 5 
Câu 4. [ Mức độ 1] Giới hạn lim x2 3x 5 bằng
 x 2 
 A. 1. B. 2 . C. 3 . D. 4 .
 Lời giải
 FB tác giả: Nguyễn Chương 
 Trang 4 SP ĐỢT 3 TỔ 23ĐỀ KIỂM TRA 45 PHÚT-CHƯƠNG IV-GIẢI TÍCH 11
 Ta có: lim x2 3x 5 22 3.2 5 3.
 x 2 
 2x3 3x2 3x 2
Câu 5. [ Mức độ 1] Giới hạn lim bằng
 x 1 x2 1
 1 3
 A. . B. 1. C. . D. 2 .
 2 2
 Lời giải
 FB tác giả: Nguyễn Chương 
 2 2
 2x3 3x2 3x 2 x 1 2x x 2 2x x 2 3
 Ta có: lim lim lim .
 x 1 x2 1 x 1 x 1 x 1 x 1 x 1 2
 3 x2
Câu 6. [ Mức độ 2] Giới hạn lim bằng
 x 1 1 x
 3
 A. . B. . C. . D. 2 .
 2
 Lời giải
 FB tác giả: Nguyễn Chương 
 3 x2
 Ta có: lim .
 x 1 1 x
 lim 3 x2 2
 x 1 
 Vì lim 1 x 0 .
 x 1
 1 x 0, x 1
Câu 7. [NB] Hình nào trong các hình dưới đây là đồ thị của hàm số không liên tục tại x 1? 
 A. B. 
 C. D. 
 Lời giải
 FB tác giả: Đình Khang 
 Dựa vào đồ thị ta thấy đáp án D hàm số bị gián đoạn tại x 1 .
 Trang 5 SP ĐỢT 3 TỔ 23ĐỀ KIỂM TRA 45 PHÚT-CHƯƠNG IV-GIẢI TÍCH 11
Câu 8. [ NB] Hàm số nào sau đây gián đoạn tại x 2 ?
 3x 4
 A. y x3 1. B. y x4 2x2 1. C. y sin x . D. y .
 x 2
 Lời giải
 FB tác giả: Đình Khang
 Do các hàm số ở đáp án A, B, C có TXĐ D ¡ và đều liên tục trên ¡ nên liên tục tại điểm 
 x 2 .
 3x 4
 Xét hàm số y có TXĐ D ¡ \ 2 
 x 2
 3x 4 3x 4
 Ta có lim và lim nên hàm số gián đoạn tại x 2 .
 x 2 x 2 x 2 x 2
 x2 7x 12
 khi x 3
Câu 9. [TH] Cho hàm số y x 3 . Tìm giá trị của tham số m để hàm số liên 
 2m 1 khi x 3
 tục tại điểm x 3.
 A. m 1. B. m 2 . C. m 0 D. m 1.
 Lời giải
 FB tác giả: Đình Khang
 Ta có:
 x2 7x 12 x 3 x 4 
 lim lim lim x 4 1 và f 3 2m 1. 
 x 3 x 3 x 3 x 3 x 3
 Để hàm số liên tục tại điểm x 3 thì 2m 1 1 m 1
Câu 10. [ Mức độ 1] Hàm số nào dưới đây liên tục trên khoảng ; ?
 1 2x 1
 A. y x . B. y 2 x . C. y . D. y x 7 .
 x x 7
 Lời giải
 FB tác giả: Phạm Hoài Trung 
 Hàm số đa thức liên tục trên toàn bộ tập số thực ¡ . Chọn D.
 x2 x khi x 1
Câu 11. [ Mức độ 2] Tìm m để hàm số f (x) 2 khi x 1 liên tục trên tập xác định của nó.
 mx 1 khi x 1
 A. m 2 . B. m 3 . C. m 4 . D. m 1.
 Lời giải
 FB tác giả: Phạm Hoài Trung
 Tập xác định: D ¡ .
 Khi x 1ta có: f (x) x2 x là đa thức nên f (x) liên tục trên ;1 .
 Khi x 1ta có: f (x) mx 1là đa thức nên f (x) liên tục trên 1; .
 Khi x 1ta có: f (1) 2 .
 Trang 6 SP ĐỢT 3 TỔ 23ĐỀ KIỂM TRA 45 PHÚT-CHƯƠNG IV-GIẢI TÍCH 11
 lim f (x) lim mx 1 m 1;
 x 1 x 1 
 lim f (x) lim x2 x 2 .
 x 1 x 1 
 Suy ra f (x) liên tục tại x 1khi và chỉ khi:
 lim f (x) lim f (x) f (1)
 x 1 x 1 
 m 1 2
 m 1.
 Vậy f (x) liên tục trên D ¡ khi và chỉ khi m 1.
 2x2 2x
 khi x 1
Câu 12. [ Mức độ 2] Tìm m để hàm số f (x) x 1 liên tục trên tập xác định của nó.
 5m khi x 1
 1 1 2
 A. m 1. B. m . C. m 4 , m . D. m .
 2 2 5
 Lời giải
 FB tác giả: Phạm Hoài Trung
 Tập xác định: D ¡ .
 2x2 2x
 Khi x 1ta có: f (x) là hàm phân thức hữu tỉ có tập xác định là ;1  1; 
 x 1
 nên f (x) liên tục trên mỗi khoảng ;1 và 1; .
 Khi x 1ta có: f (1) 5m .
 2x2 2x 2x(x 1)
 lim f (x) lim lim lim 2x 2 ;
 x 1 x 1 x 1 x 1 x 1 x 1
 Ta có f (x) liên tục tại x 1khi và chỉ khi:
 lim f (x) f (1)
 x 1
 5m 2
 2
 m .
 5
 2
 Vậy f (x) liên tục trên D ¡ khi và chỉ khi m .
 5
 x 2 2
Câu 13. [ Mức độ 2] Giới hạn lim bằng
 x 2 x 2
 1 1
 A. . B. .C. 0 . D. 1.
 2 4
 Lời giải
 FB tác giả: Huyền Kem 
 x 2 2 x 2 2 x 2 2 x 2 1 1
 lim lim lim lim 
 x 2 x 2 x 2 x 2 x 2 2 x 2 x 2 x 2 2 x 2 x 2 2 4
 Trang 7 SP ĐỢT 3 TỔ 23ĐỀ KIỂM TRA 45 PHÚT-CHƯƠNG IV-GIẢI TÍCH 11
 x2 4x 3
 , x 1
Câu 14. [ Mức độ 3] Với giá trị nào của tham số m thì hàm số f x 1 x2 có giới hạn tại 
 2x m, x 1
 x 1.
 A. m 3 . B. m 1. C. m 0 . D. m 1.
 Lời giải
 FB tác giả: Huyền Kem 
 Ta có, 
 x2 4x 3 x 1 x 3 3 x
 lim f x lim 2 lim lim 1.
 x 1 x 1 1 x x 1 1 x 1 x x 1 1 x
 lim f x lim 2x m 2 m
 x 1 x 1 
 Hàm số có giới hạn tại x 1 . lim f x lim f x 1 2 m m 1.
 x 1 x 1 
 x 4 2
 , x 0
 x
Câu 15. [ Mức độ 3] Có bao nhiêu giá trị của tham số m để hàm số f x có giới 
 1
 mx m2 , x 0
 4
 hạn tại x 0 .
 A. 0 . B. 2 . C. 1. D. 3 .
 Lời giải
 FB tác giả: Huyền Kem 
 Ta có, 
 x 4 2 x 4 2 x 4 2 1 1
 lim f x lim lim lim 
 x 0 x 0 x x 0 x x 4 2 x 0 x 4 2 4
 1 1
 lim f x lim mx m2 m2 
 x 0 x 0 4 4
 1 1
 Để hàm số có giới hạn tại x 0 thì lim f x lim f x m2 m 0 . Vậy có một 
 x 0 x 0 4 4
 giá trị m thảo mãn. 
II. PHẦN 2: TỰ LUẬN (2,5 ĐIỂM)
 4x 1 1
 khi x 0
Câu 16. [ Mức độ 2] Tìm các giá trị của tham số a để hàm số f (x) ax2 (2a 1)x liên 
 3 khi x=0
 tục tại x 0 .
 Lời giải
 FB tác giả: Bình Yên 
 Trang 8 SP ĐỢT 3 TỔ 23ĐỀ KIỂM TRA 45 PHÚT-CHƯƠNG IV-GIẢI TÍCH 11
 4x 1 1 4 2
 Ta có lim f (x) lim lim 
 x 0 x 0 x ax 2a 1 x 0 ax 2a 1 4x 1 1 2a 1
 2 1
 Hàm số liên tục tại x 0 3 a .
 2a 1 6
 1 1 1 
Câu 17. [ Mức độ 3] Tính lim ... .
 1.3 2.4 n. n 2 
 Lời giải
 FB tác giả: Bình Yên 
 1 1 1 1 2 2 2 
 lim ... lim ... 
 1.3 2.4 n. n 2 2 1.3 2.4 n. n 2 
 1 1 1 1 1 1 1 1 1 1 1 3
 lim 1 ... lim 1 .
 2 3 2 4 3 5 n n 2 2 2 n 2 4
 ax2 (a 2)x 2
 khi x 1
Câu 18. [ Mức độ 3] Cho hàm số f (x) x 3 2 . Tìm các giá trị nguyên của a để 
 2
 8 a khi x=1
 hàm số liên tục tại x 1.
 Lời giải
 FB tác giả: Bình Yên 
 ax2 (a 2)x 2 x 1 ax 2 
 lim lim lim ax 2 x 3 2 4a 8
 x 1 x 3 2 x 1 x 3 2 x 1 
 2 a 0
 Hàm số liên tục tại x 1 lim f (x) f (1) 4a 8 8 a .
 x 1 a 4
 Trang 9