Đề kiểm tra 15 phút môn Hình học Lớp 11 - Chủ đề: Đường thẳng và mặt phẳng trong không gian - Năm học 2020-2021 (Có đáp án)

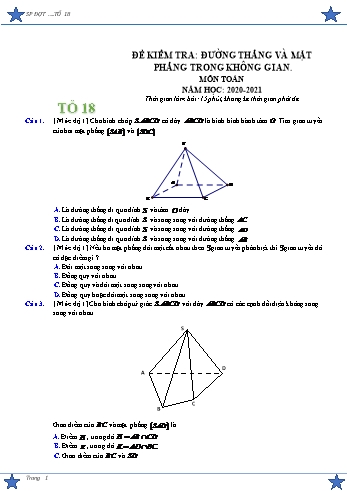
 SP ĐỢT ..TỔ 18 
 ĐỀ KIỂM TRA: ĐƯỜNG THẲNG VÀ MẶT 
 PHẲNG TRONG KHÔNG GIAN.
 MÔN TOÁN
 NĂM HỌC: 2020-2021
 Thời gian làm bài: 15 phút, không kể thời gian phát đề
 TỔ 18
Câu 1. [ Mức độ 1] Cho hình chóp S.ABCD có đáy ABCD là hình bình hành tâm O . Tìm giao tuyến 
 của hai mặt phẳng SAB và SDC .
 S
 A D
 B C
 A. Là đường thẳng đi qua đỉnh S và tâm O đáy.
 B. Là đường thẳng đi qua đỉnh S và song song với đường thẳng AC .
 C. Là đường thẳng đi qua đỉnh S và song song với đường thẳng AD .
 D. Là đường thẳng đi qua đỉnh S và song song với đường thẳng AB .
Câu 2. [ Mức độ 1] Nếu ba mặt phẳng đôi một cắt nhau theo 3 giao tuyến phân biệt thì 3 giao tuyến đó 
 có đặc điểm gì ?
 A. Đôi một song song với nhau.
 B. Đồng quy với nhau.
 C. Đồng quy và đôi một song song với nhau.
 D. Đồng quy hoặc đôi một song song với nhau.
Câu 3. [ Mức độ 1] Cho hình chóp tứ giác S.ABCD với đáy ABCD có các cạnh đối diện không song 
 song với nhau.
 S
 D
 A
 C
 B
 Giao điểm của BC và mặt phẳng SAD là
 A. Điểm H , trong đó H AB CD .
 B. Điểm K , trong đó K AD  BC .
 C. Giao điểm của BC và SD .
 Trang 1 SP ĐỢT ..TỔ 18 
 D. Giao điểm của BC và SA .
Câu 4. [ Mức độ 1] Cho hình chóp tứ giác S.ABCD với đáy ABCD có các cạnh đối diện không song 
 song với nhau và M là một điểm trên cạnh SA .
 S
 M
 D
 A
 C
 B
 Giao điểm của AB và mặt phẳng MCD là
 A. Điểm H , trong đó H AB CD .
 B. Điểm K , trong đó K AD  BC .
 C. Giao điểm của AB và MD .
 D. Giao điểm của AB và MC .
Câu 5. [ Mức độ 2] Cho tứ diện ABCD . Điểm M thuộc đoạn AC . Mặt phẳng qua M song song 
 với AB và AD. Thiết diện của với tứ diện ABCD là hình gì?
 A. Hình tam giác.B. Hình bình hành.
 C. Hình thang.D. Hình ngũ giác.
Câu 6. [ Mức độ 2] Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. M là một điểm thuộc 
 đoạn SB . Mặt phẳng ADM cắt hình chóp S.ABCD theo thiết diện là 
 A. Hình thang. B. Hình chữ nhật. C. Hình bình hành. D. Tam giác.
Câu 7. [ Mức độ 2] Cho tứ diện ABCD , gọi G1,G2 lần lượt là trọng tâm tam giác BCD và ACD . Mệnh 
 đề nào sau đây sai?
 A. G1G2 // ABD . B. Ba đường thẳng BG1, AG2 và CD đồng quy. 
 2
 C. G G // ABC . D. G G AB .
 1 2 1 2 3
Câu 8. [ Mức độ 2] Cho tứ diện ABCD. Gọi G là trọng tâm tam giác BCD, M là trung điểm CD, I 
 là điểm ở trên đoạn thẳng AG, BI cắt mặt phẳng ACD tại J. Khẳng định nào sau đây sai?
 A. AM ACD  ABG . B. A, J, M thẳng hàng.
 C. J là trung điểm của AM. D. DJ ACD  BDJ . 
Câu 9: [ Mức độ 3 ] Cho hình chóp S.ABCD , đáy ABCD là hình bình hành có tâm O . Gọi I là 
 trung điểm của SC . Mặt phẳng P chứa AI và song song với BD , cắt SB, SD lần lượt tại 
 M và N . Khẳng định nào sau đây đúng?
 SM 3 SN 1 SM SN 1 MB 1
 A. . B. . C. . D. .
 SB 4 SD 2 SB SD 3 SB 3
 Trang 2 SP ĐỢT ..TỔ 18 
Câu 10. [Mức độ 4] Cho tứ diện ABCD . Gọi M , N, P lần lượt thuộc các cạnh AB, AC, AD sao cho 
 AM 2MB, AN NC, AP 3PD . Gọi I là trung điểm của đường trung tuyến DQ trong tam 
 AI
 giác BCD , S là giao điểm của mặt phẳng MNP và AI . Tính tỉ số .
 AS
 1 4 37
 A. B. C. D. 2
 2 3 24
 ----------Hết----------
 Trang 3 SP ĐỢT ..TỔ 18 
 HƯỚNG DẪN GIẢI: ĐƯỜNG THẲNG VÀ 
 MẶT PHẲNG TRONG KHÔNG GIAN.
 MÔN TOÁN
 NĂM HỌC: 2020-2021
 Thời gian làm bài: 15 phút, không kể thời gian phát đề
 TỔ 18
Câu 1. [ Mức độ 1] Cho hình chóp S.ABCD có đáy ABCD là hình bình hành tâm O . Tìm giao tuyến 
 của hai mặt phẳng SAB và SDC .
 S
 A D
 B C
 A. Là đường thẳng đi qua đỉnh S và tâm O đáy.
 B. Là đường thẳng đi qua đỉnh S và song song với đường thẳng AC .
 C. Là đường thẳng đi qua đỉnh S và song song với đường thẳng AD .
 D. Là đường thẳng đi qua đỉnh S và song song với đường thẳng AB .
 Lời giải
 FB tác giả: Ngoc Unicom 
 Xét hai mặt phẳng SAB và SDC có S chung và AB//CD .
 Nên giao tuyến của hai mặt phẳng SAB và SDC là đường thẳng đi qua đỉnh S và song 
 song với đường thẳng AB .
Câu 2. [ Mức độ 1] Nếu ba mặt phẳng đôi một cắt nhau theo 3 giao tuyến phân biệt thì 3 giao tuyến đó 
 có đặc điểm gì ?
 A. Đôi một song song với nhau.
 B. Đồng quy với nhau.
 C. Đồng quy và đôi một song song với nhau.
 D. Đồng quy hoặc đôi một song song với nhau.
 Lời giải
 FB tác giả: Ngoc Unicom 
 Theo định lí về giao tuyến của hai mặt phẳng: Nếu ba mặt phẳng đôi một cắt nhau theo ba 
 giao tuyến phân biệt thì ba giao tuyến ấy hoặc đồng quy hoặc đôi một song song.
Câu 3. [ Mức độ 1] Cho hình chóp tứ giác S.ABCD với đáy ABCD có các cạnh đối diện không song 
 song với nhau.
 Trang 4 SP ĐỢT ..TỔ 18 
 S
 D
 A
 C
 B
 Giao điểm của BC và mặt phẳng SAD là
 A. Điểm H , trong đó H AB CD .
 B. Điểm K , trong đó K AD  BC .
 C. Giao điểm của BC và SD .
 D. Giao điểm của BC và SA .
 Lời giải
 FB tác giả: Nguyen Quoc Qui 
 Xét mặt phẳng ABCD kéo dài BC cắt AD tại K 
Câu 4. [ Mức độ 1] Cho hình chóp tứ giác S.ABCD với đáy ABCD có các cạnh đối diện không song 
 song với nhau và M là một điểm trên cạnh SA .
 S
 M
 D
 A
 C
 B
 Giao điểm của AB và mặt phẳng MCD là
 A. Điểm H , trong đó H AB CD .
 B. Điểm K , trong đó K AD  BC .
 C. Giao điểm của AB và MD .
 D. Giao điểm của AB và MC .
 Lời giải
 FB tác giả: Nguyen Quoc Qui 
 Trang 5 SP ĐỢT ..TỔ 18 
 S
 M
 D
 A
 C
 B
 H
 Xét mặt phẳng ABCD kéo dài AB cắt CD tại H 
Câu 5. [ Mức độ 2] Cho tứ diện ABCD . Điểm M thuộc đoạn AC . Mặt phẳng qua M song song 
 với AB và AD. Thiết diện của với tứ diện ABCD là hình gì?
 A. Hình tam giác.B. Hình bình hành.
 C. Hình thang.D. Hình ngũ giác.
 Lời giải
 FB tác giả: Thuy Nguyen
 A
 M
 B D
 N P
 C
 • và ABC có M chung,
 song song với AB , AB  ABC .
  ABC Mx, Mx / / AB và Mx  BC N .
 • và ACD có M chung,
 song song với AD, AD  ACD 
  ACD My, My / / AD và My CD P .
 Ta có:  ABC MN .
  ACD MP .
  BCD NP .
 Thiết diện của với tứ diện ABCD là tam giác MNP .
 Trang 6 SP ĐỢT ..TỔ 18 
Câu 6. [ Mức độ 2] Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. M là một điểm thuộc 
 đoạn SB . Mặt phẳng ADM cắt hình chóp S.ABCD theo thiết diện là 
 A. Hình thang. B. Hình chữ nhật. C. Hình bình hành. D. Tam giác.
 Lời giải
 FB tác giả: Thuy Nguyen
 S
 M
 G
 A B
 D C
 Do BC // AD nên mặt phẳng ADM và SBC có giao tuyến là đường thẳng MG song song
 với BC . Thiết diện là hình thang AMGD .
Câu 7. [ Mức độ 2] Cho tứ diện ABCD , gọi G1,G2 lần lượt là trọng tâm tam giác BCD và ACD . Mệnh 
 đề nào sau đây sai?
 A. G1G2 // ABD . B. Ba đường thẳng BG1, AG2 và CD đồng quy. 
 2
 C. G G // ABC . D. G G AB .
 1 2 1 2 3
 Lời giải
 FB tác giả: Tô Lê Diễm Hằng
 Gọi M là trung điểm của CD . 
 G G // AB
 MG MG 1 1 2
 Xét ABM ta có: 1 2 1 D sai.
 MB MA 3 G G AB
 1 2 3
 Vì G1G2 // AB G1G2 // ABD A đúng.
 Vì G1G2 // AB G1G2 // ABC C đúng.
 Ba đường BG1, AG2 ,CD , đồng quy tại M B đúng.
 Trang 7 SP ĐỢT ..TỔ 18 
Câu 8. [ Mức độ 2] Cho tứ diện ABCD. Gọi G là trọng tâm tam giác BCD, M là trung điểm CD, I 
 là điểm ở trên đoạn thẳng AG, BI cắt mặt phẳng ACD tại J. Khẳng định nào sau đây sai?
 A. AM ACD  ABG . B. A, J, M thẳng hàng.
 C. J là trung điểm của AM. D. DJ ACD  BDJ . 
 Lời giải
 FB tác giả: Tô Lê Diễm Hằng
 A
 J
 I
 B D
 G
 M
 C
 Ta có A là điểm chung thứ nhất giữa hai mặt phẳng ACD và GAB . 
 M BG  ABG M ABG 
 Do BG CD M M là điểm chung thứ hai giữa hai 
 M CD  ACD M ACD 
 mặt phẳng ACD và GAB .
 ABG  ACD AM  A đúng.
 BI  ABG 
 Ta có AM  ABM AM , BI đồng phẳng.
 ABG  ABM 
 J BI  AM A, J, M thẳng hàng  B đúng.
 DJ  ACD 
 Ta có DJ ACD  BDJ  D đúng.
 DJ  BDJ 
 Điểm I di động trên AG nên J có thể không phải là trung điểm của AM
  C sai.
Câu 9: [ Mức độ 3 ] Cho hình chóp S.ABCD , đáy ABCD là hình bình hành có tâm O . Gọi I là 
 trung điểm của SC . Mặt phẳng P chứa AI và song song với BD , cắt SB, SD lần lượt tại 
 M và N . Khẳng định nào sau đây đúng?
 SM 3 SN 1 SM SN 1 MB 1
 A. . B. . C. . D. .
 SB 4 SD 2 SB SD 3 SB 3
 Lời giải
 FB tác giả : Thi Xuan Nguyen
 Trang 8 SP ĐỢT ..TỔ 18 
 Gọi E là giao điểm của AI với SO , kẻ đường thẳng qua E song song với BD và cắt SB, SD 
 lần lượt tại M , N . Khi đó P  AMIN .
 OE 1
 Dễ thầy E là trọng tâm SAC nên .
 SO 3
 MB OE 1
 Từ MN //BD ta được .
 SB SO 3
Câu 10. [Mức độ 4] Cho tứ diện ABCD . Gọi M , N, P lần lượt thuộc các cạnh AB, AC, AD sao cho 
 AM 2MB, AN NC, AP 3PD . Gọi I là trung điểm của đường trung tuyến DQ trong tam 
 AI
 giác BCD , S là giao điểm của mặt phẳng MNP và AI . Tính tỉ số .
 AS
 1 4 37
 A. B. C. D. 2
 2 3 24
 FB tác giả: Xuyen Tran 
 Lời giải
 Bổ đề: Cho tam giác ABC , có trung tuyến AM . Lấy P,Q lần lượt thuộc AB, AC , gọi I là 
 AB AC AM
 giao điểm của AM , PQ . Khi đó ta có đẳng thức 2 .
 AP AQ AI
 Chứng minh bổ đề:
 Gọi B ,C là các điểm trên đường AM sao cho BB ,CC 
 đều song song với PQ . Khi đó ta dễ thấy MB MC . Từ 
 đây kết hợp với định lý Talet và một số biến đổi ta có 
 ngay: 
 AB AC AB AC AB AC 
 AP AQ AI AI AI
 AM MB AM MC 2AM
 AI AI
 Bổ đề đã được chứng minh.
 Bây giờ trở lại bài toán ban đầu:
 Trang 9 SP ĐỢT ..TỔ 18 
 Gọi T là giao điểm của MN với AQ . Khi đó điểm S 
 trong giả thiết chính là giao điểm của TP với AI .
 Vận dụng bổ để ta có:
 AQ 1 AB AC 1 3 2 7
 AT 2 AM AN 2 2 1 4
 Tiếp tục vận dụng bổ đề ta có: 
 AI 1 AQ AD 1 7 4 37
 .
 AS 2 AT AP 2 4 3 24
 ----------Hết----------
Trang 10