Đề cương ôn THPTQG môn Toán - Chủ đề: Hàm số (Mức 4) - Năm học 2019- 2020

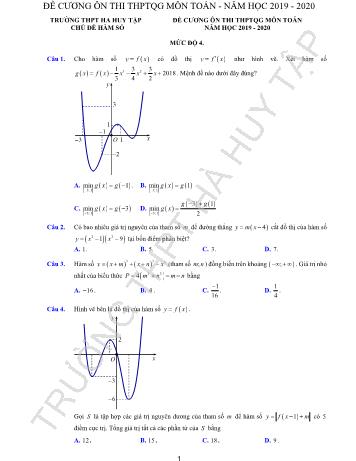
TRƯỜNG THPT HA HUY TẬP ĐỀ CƯƠNG ÔN THI THPTQG MÔN TOÁN 
CHỦ ĐỀ HÀM SỐ NĂM HỌC 2019 - 2020 
MỨC ĐỘ 4. 
Câu 1. Cho hàm số y f x có đồ thị y f x như hình vẽ. Xét hàm số 
 3 2
1 3 3
2018
3 4 2
g x f x x x x . Mệnh đề nào dưới đây đúng? 
A. 
 
3; 1
min 1g x g
 . B. 
 
3; 1
min 1g x g
C. 
 
3; 1
min 3g x g
 D. 
 
3; 1
3 1
min
2
g g
g x
Câu 2. Có bao nhiêu giá trị nguyên của tham số m để đường thẳng 4y m x cắt đồ thị của hàm số 
 2 21 9y x x tại bốn điểm phân biệt? 
A. 1. B. 5. C. 3. D. 7. 
Câu 3. Hàm số 
3 3 3y x m x n x (tham số ;m n ) đồng biến trên khoảng ; . Giá trị nhỏ 
nhất của biểu thức 2 24P m n m n bằng 
A. 16 . B. 4 . C. 
1
16
. D. 
1
4
. 
Câu 4. Hình vẽ bên là đồ thị của hàm số y f x . 
Gọi S là tập hợp các giá trị nguyên dương của tham số m để hàm số 1y f x m có 5 
điểm cực trị. Tổng giá trị tất cả các phần tử của S bằng 
A. 12 . B. 15 . C. 18 . D. 9 . 
O x
y
2
3 
6 
O x
y
1
1
3
3 
1 
2 
ĐỀ CƯƠNG ÔN THI THPTQG MÔN...ỏa mãn 
yêu cầu bài toán? 
A. 0 . B. 1. C. 3 . D. 2 . 
Câu 12. Cho các số thực dương x , y . Tìm giá trị lớn nhất của biểu thức 
2
3
2 2
4
4
xy
P
x x y
A. max 1P . B. 
1
max
10
P . C. 
1
max
8
P . D. 
1
max
2
P . 
Câu 13. Cho hàm số y f x có đồ thị y f x cắt trục Ox tại ba điểm có hoành độ a b c như 
hình vẽ. 
Khẳng định nào dưới đây có thể xảy ra? 
A. f a f b f c . B. f b f a f c . 
C. f c f a f b . D. f c f b f a 
Câu 14. Một sợi dây có chiều dài là 6 m , được chia thành hai phần. Phần thứ nhất được uốn thành hình 
tam giác đều, phần thứ hai uốn thành hình vuông. Hỏi độ dài của cạnh hình tam giác đều bằng 
bao nhiêu để diện tích hai hình thu được là nhỏ nhất? 
A. 
18 3
m .
4 3 
 B. 
12
m .
4 3 
 C. 
18
m .
9 4 3 
 D. 
36 3
m .
4 3 
O x
y
a b c
ĐỀ CƯƠNG ÔN THI THPTQG MÔN TOÁN - NĂM HỌC 2019 - 2020
3
Câu 15. (THPT Nguyễn Khuyến-Nam Định-lần 1-năm 2017-2018) Cho x , y là các số thực thỏa mãn 
1 2 2x y x y . Gọi M , m lần lượt là giá trị lớn nhất và nhỏ nhất của 
 2 2 2 1 1 8 4P x y x y x y . Tình giá trị M m . 
A. 41. B. 44 . C. 42 . D. 43 . 
Câu 16. Tìm m để hàm số 
2 cot 1
cot
x
y
x m
 đồng biến trên khoảng ;
4 2
? 
A. ; 2m . B. 
1
; 1 0;
2
m
  
. 
C. 2;m . D. 
1
;
2
m
. 
Câu 17. Hàm số 4 28 8 1f x x x đạt giá trị lớn nhất trên đoạn  1; 1 tại bao nhiêu giá trị của x ? 
A. 3 . B. 2 . C. 5 . D. 4 . 
Câu 18. Cho x , y là những số thực thoả mãn 2 2 1x xy y . Gọi M và m lần lượt là giá trị lớn nhất 
và giá trị nhỏ nhất của 
4 4
2 2
1
1
x y
P
x y
. Giá trị của 15A M m là 
A. 17 2 6A . B. 17 6A . C. 17 2 6A . D. 17 6A . 
Câu 19. Tìm tất cả những giá trị thực của m để bất phương trình sau có nghiệm với mọi x thuộc tập xác 
định. 4 42 2 2 6 2 6x x x x m . 
A. 4 12 2 3m . B. 6 3 2m . C. 4 12 2 3m . D. 42 6 2 6m . 
Câu 20. Nhà xe khoán cho hai tài xế ta-xi An và Bình mỗi người lần lượt nhận 32 lít và 72 lít xăng. Hỏi 
tổng số ngày ít nhất là bao nhiêu để hai tài xế chạy tiêu t...MN ngắn nhất bằng: 
A. 8 2 . B. 2017 . C. 8 . D. 4 . 
O x
y
42
1
O x
y
2
4
ĐỀ CƯƠNG ÔN THI THPTQG MÔN TOÁN - NĂM HỌC 2019 - 2020
5
Câu 29. Cho hàm số 
2
2
1
4 9
ax x
y
x bx
 có đồ thị C , trong đó a , b là các hằng số dương thỏa mãn 
. 4 a b . Biết rằng C có đường tiệm cận ngang y c và có đúng 1 đường tiệm cận đứng. Tính 
tổng 3 24 T a b c . 
A. 11 T . B. 4 T . C. 7 T . D. 11 T . 
Câu 30. Cho hàm số f x có đạo hàm trên và có đồ thị của hàm y f x như hình vẽ. Biết rằng 
 0 3 2 5 f f f f . Giá trị nhỏ nhất và giá trị lớn nhất của f x trên đoạn  0;5 lần 
lượt là: 
A. 0f , 5f . B. 2f , 0f . C. 1f , 3f . D. 2f , 5f . 
Câu 31. Cho hàm số f x xác định trên và có đồ thị f x như hình vẽ. Đặt g x f x x . Hàm 
số g x đạt cực đại tại điểm nào sau đây? 
A. 2 x . B. 0 x . C. 1 x . D. 1 x . 
Câu 32. Xét các số thực dương x , y thỏa mãn 
1 2
ln 3 1
x
x y
x y
. Tìm giá trị nhỏ nhất minP của 
1 1
 P
x xy
. 
A. min 8 P . B. min 4 P . C. min 2 P . D. min 16 P . 
Câu 33. Cho hàm số f x có đạo hàm liên tục trên và có đồ thị của hàm y f x như hình vẽ. Xét 
hàm số 2( ) 2 g x f x . Mệnh đề nào dưới đây sai? 
A. Hàm số ( )g x đồng biến trên 2; . B. Hàm số ( )g x nghịch biến trên 0;2 . 
C. Hàm số ( )g x nghịch biến trên 1;0 . D. Hàm số ( )g x nghịch biến trên ; 2 . 
y
xO 2 5
1 
O1 1 2 x
1
2
y
O
y
x1 2
4 
1
2 
ĐỀ CƯƠNG ÔN THI THPTQG MÔN TOÁN - NĂM HỌC 2019 - 2020
6
Câu 34. Hàm số y f x có đồ thị y f x như hình vẽ. 
Xét hàm số 3 2
1 3 3
2017
3 4 2
g x f x x x x . Trong các mệnh đề dưới đây: 
 I 0 1g g . II 
 
3;1
min 1
x
g x g
 . 
 III Hàm số nghịch biến trên 3; 1 . IV 
 
 
3;1
max max 3 , 1
x
g x g g
 . 
Số mệnh đề đúng là: 
A. 4. B. 3. C. 2. D. 1. 
Câu 35. Một công ty bất động sản có 50 căn hộ cho thuê. Biết rằng nếu cho thuê mỗi căn hộ với giá 
2.000.000 đồng một tháng thì mọi căn hộ đều có người thuê và cứ mỗi lần tăng giá cho thuê, mỗi 
căn hộ thêm 50.000 đồng một tháng thì có thêm một căn hộ bị b