Đề cương ôn tập giữa kì II môn Toán Lớp 11 - Năm học 2020-2021 - Trường THPT Chu Văn An (Có đáp án)

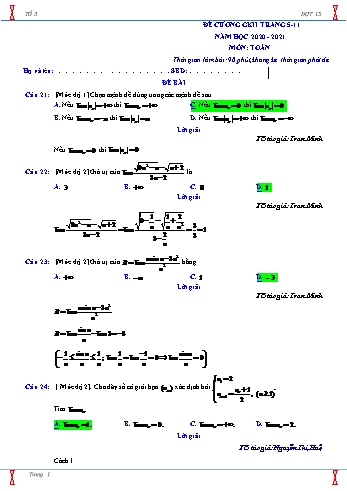
 TỔ 3 ĐỢT 15
 ĐỀ CƯƠNG GKII TRANG 5-11 
 NĂM HỌC 2020 - 2021
 MễN: TOÁN 
 Thời gian làm bài: 90 phỳt, khụng kể thời gian phỏt đề
Họ và tờn: .. SBD: .
 ĐỀ BÀI 
 Cõu 21: [Mức độ 1] Chọn mệnh đề đỳng trong cỏc mệnh đề sau
 A. Nếu lim un thỡ limun . C. Nếu lim un 0 thỡ lim un 0 .
 B. Nếu limun a thỡ lim un a . D. Nếu lim un thỡ limun .
 Lời giải
 FB tỏc giả: Tran Minh
 Nếu lim un 0 thỡ lim un 0 .
 9n2 n n 2
 Cõu 22: [Mức độ 2] Giỏ trị của lim là
 3n 2
 A. 3. B. . C. 0 . D. 1.
 Lời giải
 FB tỏc giả: Tran Minh
 1 1 2
 9 
 9n2 n n 2 2 3
 lim lim n n n 1.
 2
 3n 2 3 3
 n
 nsin n 3n2
 Cõu 23: [Mức độ 2] Giỏ trị của B lim bằng
 n2
 A. . B. . C. 1. D. - 3.
 Lời giải
 FB tỏc giả: Tran Minh
 nsin n 3n2
 B lim .
 n2
 sin n
 B lim lim3 3.
 n
 1 sin n 1 1 1 sin n 
 ; lim lim 0 lim 0 .
 n n n n n n 
 u 2
 1
 Cõu 24: [ Mức độ 2]. Cho dóy số cú giới hạn (un ) xỏc định bởi u 1 .
 u n , (n 1)
 n 1 2
 Tỡm limun .
 A. limun 1. B. limun 0. C. limun . D. limun 2.
 Lời giải
 FB tỏc giả: Nguyễn Thị Huệ
 Cỏch 1.
 Trang 1 TỔ 3 ĐỢT 15
 u 1
 Từ giả thiết u n 2u u 1 2(u 1) u 1.
 n 1 2 n 1 n n 1 n
 vn 1 1
 Đặt vn un 1 2vn 1 vn .
 vn 2
 v 1
 1
 Do đú (vn ) là một cấp số nhõn cú 1 .
 q 
 2
 n 1 n 1
 n 1 1 1 
 Suy ra vn v1.q un vn 1 1.
 2 2 
 n 1
 1 
 Vậy limun lim 1 1.
 2 
 Cỏch 2.
 Gọi limun a limun 1 a .
 u 1 a 1
 Do u n nờn a a 1.
 n 1 2 2
 1 3 n 
 1 ... 
 2 2 2 
Cõu 25: [ Mức độ 2]. Tớnh I lim 2 .
 n 1 
 1 1 1
 A. I . B. I . C. I . D. I 1.
 4 2 8
 Lời giải
 FB tỏc giả: Nguyễn Thị Huệ
 Ta cú, 
 1 3 n 1 1
 1 ... (1 2 3... n) 2 1 
 n(n 1) n n 1
 lim 2 2 2 lim 2 lim lim lim n .
 2 2 2 2 4
 n 1 n 1 4(n 1) 4n 4 4 4
 n2
 1 1 1 
Cõu 26: [ Mức độ 3 ]. Tớnh I lim ... .
 n2 n 1 n2 n 2 n2 2n 
 A. I . B. I 3 . C. I 2 . D. I 1.
 Lời giải
 FB tỏc giả: Nguyễn Thị Huệ
 1 1 1
 Ta cú ,k 2,3,...,n 1
 n2 2n n2 n k n2 n 1
 n 1 1 1 n
 ... 
 n2 2n n2 n 1 n2 n 2 n2 2n n2 n 1
 n 1 n 1
 Mà lim lim 1; lim lim 1.
 2 2 2 1 1
 n 2n 1 n n 1 1 
 n n n2
 Vậy I 1.
 Trang 2 TỔ 3 ĐỢT 15
 n 1
 khi n chaỹn
 100n 1
Cõu 27: [Mức độ 2] Cho dóy số un xỏc định bởi un . Tỡm cỏc mệnh đề đỳng 
 1
 khi n leỷ
 n
 trong cỏc mệnh đề sau.
 A. limun 0 .
 1
 B. limu 0 với n lẻ và limu với n chẵn.
 n n 100
 C. limun khụng tồn tại.
 1
 D. limu .
 n 100
 Lời giải
 FB tỏc giả: Lờ Duy Lực
 1
 Giới hạn của dóy số nếu cú là duy nhất mà khi n lẻ thỡ limu 0 và khi n chẵn. Dolimu 
 n n 100
 nờn limun khụng tồn tại.
 2n 2
Cõu 28: [Mức độ 2] Kết quả của lim n 1 là
 n4 n2 1
 A. 1. B. 0 . C. . D. .
 Lời giải
 FB tỏc giả: Lờ Duy Lực
 3
 1 
 3 2 1 
 2n 2 2 n 1 1 n
 Ta cú lim n 1 lim lim . 0 .
 n4 n2 1 n4 n2 1 n 1 1 
 1 2 4 
 n n 
 2n 2
Cõu 29: [Mức độ 2] Cho dóy số u cú u n 1 . Tớnh I limu .
 n n 100n4 n2 1 n
 1 1
 A. . B. 0 . C. I . D. I .
 10000 100
 Lời giải
 FB tỏc giả: Lờ Duy Lực
 3
 1 
 3 2 1 
 2n 2 2 n 1 1 n
 Ta cú lim n 1 lim lim 0.
 100n4 n2 1 100n4 n2 1 n 1 1 
 100 2 4 
 n n 
 bn2 3bn b
Cõu 30: [ Mức độ 2] Cho dóy số u với u . Tỡm tất cả cỏc giỏ trị của b để dóy số (u )
 n n 5n2 2n 2b n
 cú giới hạn hữu hạn.
 A. Khụng cú giỏ trị nào của b thỏa món. B. b là một số thực tựy ý.
 C. b nhận giỏ trị nguyờn duy nhất là 2. D. b là một số thực tựy ý khỏc0.
 Trang 3 TỔ 3 ĐỢT 15
 Lời giải
 FB tỏc giả: Thanh Loan
 3
 3n
 Nếu b 0 limu lim lim n 0 .
 n 2 2
 5n 2n 5 
 n
 3 b
 2 b 
 bn 3n b 2 b
 Nếu b 0 limu lim lim n n .
 n 2 2 b
 5n 2n 2b 5 2 5
 n n2
 Như vậy với mọi số thực b thỡ dóy số un đều cú giới hạn hữu hạn.
 CHUYấN ĐỀ 3. ĐƯỜNG THẲNG SONG SONG VỚI MẶT PHẲNG
Cõu 1: [ Mức độ 1] Cho cỏc giả thiết sau, giả thiết nào kết luận đường thẳng a// P ?
 A. a  (P)  . B. a// b và b// (P) .
 C. a// b và b  (P) . D. a// b , b  c l và P mp b,c .
 Lời giải
 FB tỏc giả: ThanhLoan
 Theo định nghĩa a// P a  (P)  .
Cõu 2: [ Mức độ 1] Tỡm mệnh đề đỳng trong cỏc mệnh đề sau:
 A. Hai đường thẳng chộo nhau thỡ khụng cú điểm chung.
 B. Hai đường thẳng khụng song song thỡ chộo nhau.
 C. Hai đường thẳng khụng song song và khụng cắt nhau thỡ chộo nhau.
 D. Hai đường thẳng khụng cú điểm chung thỡ song song với nhau.
 Lời giải
 FB tỏc giả: ThanhLoan
 Đỏp ỏn B sai vỡ hai đường thẳng khụng cú điểm chung cú thể song song với nhau.
 Đỏp ỏn C sai vỡ hai đường thẳng khụng song song và khụng cắt nhau thỡ cú thể chộo nhau.
 Đỏp ỏn D sai vỡ hai đường thẳng khụng cú điểm chung thỡ cú thể song song hoặc chộo nhau.
Cõu 3: [Mức độ 1] Cho hỡnh chúp S.ABCD , đỏy ABCD là hỡnh thang với đỏy AB,CD . Gọi E, F lần 
 lượt là trung điểm của AD, BC . Giao tuyến của hai mặt phẳng SAB và SCD là:
 A. Đường thẳng qua S và song song với AD .
 B. Đường thẳng qua S và song song với EF .
 C. Đường thẳng qua S và song song với AF .
 D. Đường thẳng qua S và giao điểm của cặp đường thẳng AB, SC .
 Lời giải
 FB tỏc giả: Thanh Mai Nguyen
 Trang 4 TỔ 3 ĐỢT 15
 S
 d
 A B
 E
 F
 D C
 AB  SAB 
 Ta cú: CD  SCD SAB  SCD d qua S và d P AB P CD
 AB P CD
 Theo giả thiết cú EF P AB nờn giao tuyến cần tỡm là đường thẳng d qua S và song song với EF
 .
Cõu 4: [Mức độ 1] Cho hỡnh chúp S.ABCD , O là giao điểm của AC, BD . Gọi M , N lần lượt là trung 
 điểm của SA, SC . Mặt phẳng thay đổi qua MN cắt cỏc cạnh SB, SD lần lượt tại P,Q khụng 
 trựng với cỏc đỉnh của hỡnh chúp. Xột cỏc mệnh đề sau
 (1) AC P .
 (2) P ABCD .
 (3) MN, PQ, SO đồng quy tại một điểm.
 Cỏc mệnh đề đỳng là:
 A. Chỉ (1) và (3). B. Chỉ (1) và (2). C. Chỉ (2) và (3). D. (1), (2) và (3).
 Lời giải
 FB tỏc giả: Thanh Mai Nguyen
 S
 Q
 M
 I N
 A D
 P
 O
 C
 B
 AC P MN  
 + AC P nờn A đỳng.
 AC  
 + chỉ song song với AC nờn khụng kết luận được P ABCD nờn B sai.
 Trang 5 TỔ 3 ĐỢT 15
 + MN, PQ, SO đồng quy tại I là giao điểm của MN và SO nờn C đỳng.
 Vậy cỏc mệnh đề đỳng là chỉ (1) và (3).
Cõu 5: [Mức độ 1] Cho tứ diện ABCD với M , N lần lượt là trung điểm AC, BC. Điểm E thuộc cạnh 
 DE 1
 AD sao cho , MNE cắt cạnh BD tại điểm P. Tỡm mệnh đề sai trong cỏc mệnh đề 
 DA 3
 sau:
  2  
 A. EP MN. B. ME, NP cắt nhau tại một điểm thuộc đường thẳng CD.
 3
 C. ME // NP . D. MNPE là một hỡnh thang.
 Lời giải
 Fb tỏc giả: Nguyễn Đỡnh Tõm
 MN / / AB
 MN  MNE 
 MNE  ABD EP / / AB / /MN ( P thuộc BD )
 AB  ABD 
 E MNE  ABD 
 Do đú thiết diện là hỡnh thang MNPE MN / /PE ( Đỏp ỏn D đỳng).
  1   1   2  
 MN AB và EP AB nờn EP MN (đỏp ỏn A đỳng).
 2 3 3
 BN 1 BP 2
 Vỡ NP cắt CD tại I
 BC 2 BD 3
 MNP  BCD NP
 MNP  ACD ME
 NP  ME CD I ( đỏp ỏn B đỳng, đỏp ỏn C sai).
 BCD  ACD CD
 NP CD I
Cõu 6: Cho tứ diện ABCD . Gọi I ,J lần lượt là trọng tõm cỏc tam giỏc ABC,ABD . Tỡm khẳng định sai 
 trong cỏc khẳng định sau?
 Trang 6 TỔ 3 ĐỢT 15
 A. BIJ giao với BCD theo một giao tuyến qua B và song song với CD .
 B. CD // BIJ .
 C. IJ // CD .
 D. AJ ,DI là hai đường thẳng cắt nhau.
 Lời giải
 Tỏc giả: Minh Trang; Fb: Minh Trang
 A
 E
 J
 I
 B D
 C
 EJ EI 1
 Gọi E là trung điểm AB . Xột ECD cú: IJ // CD .
 ED EC 3
 CD // BIJ 
 BIJ  BCD qua B, // CD
 Do đú khẳng định A, B, C đỳng.
 Khẳng định D sai vỡ AJ ,DI là hai đường thẳng chộo nhau.
Cõu 7: [Mức độ 2] Cho tứ diện ABCD .Trờn cỏc cạnh AD, BC lấy cỏc điểm M , N sao cho 
 MA NC 1
 , P là mặt phẳng chứa đường thẳng MN và song song với CD . Khi đú thiết diện 
 AB CD 3
 của tứ diện ABCD cắt bởi mặt phẳng P là:
 A. Một hỡnh thang với đỏy lớn gấp 3 lần đỏy nhỏ.
 B. Một hỡnh thang với đỏy lớn gấp 2 lần đỏy nhỏ.
 C. Một hỡnh bỡnh hành.
 D. Một tam giỏc.
 Lời giải
 FB tỏc giả: Ngụ Thị Thơ
 Trang 7 TỔ 3 ĐỢT 15
 Vỡ bài toỏn đỳng cho tất cả tứ diện ABCD nờn ta xột tứ diện ABCD đều cạnh a .
 Từ M vẽ đường thẳng song song CD cắt AC tại K .
 Từ N vẽ đường thẳng song song CD cắt BD tại H .
 Khi đú thiết diện của tứ diện ABCD cắt bởi mặt phẳng P là hỡnh thang MKNH .
 MK AM 1 1
 MK a.
 CD AD 3 3
 NH BN 2 2
 NH a.
 CD BC 3 3
 Vậy hỡnh thang MKNH cú đỏy lớn NH gấp 2 lần đỏy nhỏ MK . 
Cõu 8: [Mức độ 2] Cho hỡnh chúp S.ABCD cú đỏy ABCD là hỡnh bỡnh hành tõmO . Gọi M , N lần lượt 
 là trung điểm của SA, SD và I là trung điểm của OM . Xột cỏc khẳng định sau:
 1 ON // SB.
 2 BC // OMN .
 3 Thiết diện của hỡnh chúp cắt bởi OMN là hỡnh bỡnh hành.
 4 NI // SBC .
 Số khẳng định đỳng là:
 A. 3 . B. 1. C. 2 . D. 4 .
 Lời giải
 FB tỏc giả: Ngụ Thị Thơ
 +) ON / /SB (vỡ ON là đường trung bỡnh của D SBD 1 đỳng.
 Trang 8 TỔ 3 ĐỢT 15
 BC / / AD / /MN
 +) MN  OMN BC / / OMN 2 đỳng.
 BC  OMN 
 +) Hai mặt phẳng OMN và ABCD cú
 O OMN  ABCD 
 MN / / AD
 OMN  ABCD HK / /MN / / AD
 Với HK là đường thẳng qua O , song song với AD H AB, K CD 
 Thiết diện hỡnh chúp cắt bởi OMN là hỡnh thang MNKH nờn 3 sai.
 NI  OMN 
 +) NI / / SBC 4 đỳng.
 OMN / / SBC 
 Vậy cú 3 khẳng định đỳng.
Cõu 9: [Mức độ 3] Cho hỡnh chúp S.ABCD cú đỏy ABCD là hỡnh bỡnh hành. Gọi d là giao tuyến của 
 hai mặt phẳng SAD và SBC . Gọi M là trung điểm của BC , N là điểm thuộc cạnh SC sao 
 SN 1
 cho . Gọi E là giao điểm của MN và d , F là giao điểm của AE và SD . Tớnh tỉ số 
 SC 4
 S
 t FDA ?
 SFSE
 A. t 64 . B. t 6 . C. t 8 . D. t 36 .
 Lời giải
 FB tỏc giả: Trịnh Văn Thạch
 AD  SAD 
 Ta cú BC  SBC SAD  SBC d //AD .
 AD//BC
 SE SN 1 1 1 1
 Dễ thấy CMN : SEN SE CM BC AD .
 CM CN 3 3 6 6
 Trang 9 TỔ 3 ĐỢT 15
 FS FE SE 1
 Trong mp SAD : SEF : DAF .
 FD FA AD 6
 1
 FD.FA.sin ãAFD
 S FD.FA FD FA
 t FDA 2 . 36.
 S 1 FS.FE FS FE
 FSE FS.FE.sin Sã FE
 2
Cõu 10: [Mức độ 3] Cho hỡnh chúp S.ABCD cú đỏy ABCD là hỡnh bỡnh hành. Gọi M , N lần lượt là trung 
 SQ 1
 điểm của AB, AD,Q là điểm thuộc đoạn SC sao cho . Gọi R, P lần lượt là giao điểm 
 SC 3
 S
 của MNQ với đường thẳng SB và SD . Đặt t PQR . Tỡm khẳng định đỳng trong cỏc khẳng 
 SMNPQR
 định sau.
 12 4 3 4 12 3
 A. t . B. t . C. t . D. t ; ; .
 55 15 8 15 55 8
 Lời giải
 Cỏch 1:
 FB tỏc giả: Trịnh Xuõn Mạnh
 Kộo dài MN cắt BC; DC lần lượt tại I; F . Nối Q với I cắt SB tại R và nối Q với F cắt SD 
 tại P .
 1
 Ta cú AMN DFN BMI MN FN MI hay MN FI .
 3
 1
 Lại cú DN / /CI FD FC . Xột SDC ỏp dụng định lớ Menelaus ta cú:
 3
 PS FD QC PS 1 2 3
 . . 1 . . 1 PS PD .
 PD FC QS PD 3 1 2
 3
 Chứng minh tương tự ta cú SR RB .
 2
 Từ đú PR / /SB .
 Trang 10