Bài tập ôn tập Hình học Lớp 9 - Chương 1: Hệ thức lượng trong tam giác vuông

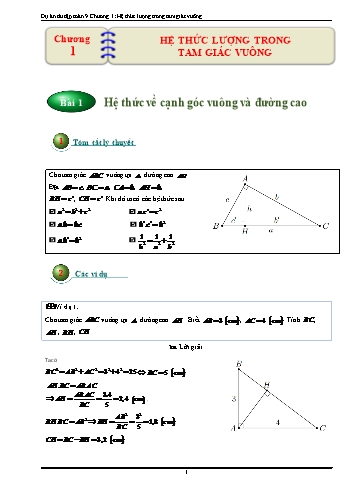
 Dự án tài tập toán 9. Chương 1: Hệ thức lượng trong tam giác vuông
 Chương HỆ THỨC LƯỢNG TRONG
 1 TAM GIÁC VUÔNG
 Bài 1 Hệ thức về cạnh góc vuông và đường cao
 Tóm tắt lý thuyết
 Cho tam giác ABC vuông tại A , đường cao AH .
 Đặt AB c , BC a , CA b , AH h , 
 BH c ', CH c '. Khi đó ta có các hệ thức sau
 2 2 2 2
  a b c  a.c ' c 
  a.h b.c  b'.c ' h2
 1 1 1
  a.b' b2  
 h2 a2 b2
 Các ví dụ
  Ví dụ 1.
 Cho tam giác ABC vuông tại A , đường cao AH . Biết AB 3 cm , AC 4 cm . Tính BC , 
 AH , BH , CH . 
  Lời giải
 Ta có 
 2 2 2 2 2
 BC AB AC 3 4 25 BC 5 cm .
 AH.BC AB.AC
 AB.AC 3.4
 AH 2,4 cm .
 BC 5
 2 2
 2 AB 3
 BH.BC AB BH 1,8 cm .
 BC 5
 CH BC BH 3,2 cm .
 1 Dự án tài tập toán 9. Chương 1: Hệ thức lượng trong tam giác vuông
  Ví dụ 2.
 Cho tam giác ABC vuông tại A , đường cao AH . ( H thuộc cạnh BC ) biết AB a , BC 2a . 
 Tính theo a độ dài AC và AH .
  Lời giải
 Theo định lí Pitago, ta có BC 2 AB2 AC 2 suy ra
 2
 AC 2 BC 2 AB2 2a a2 3a2 AC 2 a 3 . 
 Lại có AH.BC AB.AC
 AB.AC a 3
 AH .
 BC 2
  Ví dụ 3.
 Cho tam giác ABC vuông tại A , có AB 3 cm , AC 4 cm , đường cao AH . Gọi E , F là 
 hình chiếu của H lên AB , AC . Tính diện tích tứ giác AEHF .
  Lời giải
 Tứ giác AEHF có ba góc A , E , F là góc vuông 
 nên AEHF là hình chữ nhật. 
 Do đó SAEHF AE.AF .
 Ta có BC 5 cm , AH 2,4 cm nên trong các 
 tam giác vuông AHB và AHC ta có
 AH 2
 AE.AB AH 2 AE 2,76 cm .
 AB
 AH 2
 AF.AC AH 2 AF 1,44 cm .
 AC
 Suy ra SAEHF 2,76.1,44 3,9744 cm .
  Ví dụ 4.
 Cho tam giác ABC vuông tại A , đường cao AH . Biết BH 25 cm , CH 144 cm . Tính AB , 
 AC , BC , CH .
  Lời giải
 2 Dự án tài tập toán 9. Chương 1: Hệ thức lượng trong tam giác vuông
 BC BH HC 25 144 169 .
 2
 AB BH.BC 25.169 AB 65 cm .
 2
 AC CH.BC 144.169 AC 156 cm .
 2
 AH BH.CH 25.144 AH 60 cm .
  Ví dụ 5.
 25 60
 Cho tam giác ABC vuông tại A , đường cao AH . Biết BH cm , AH cm . 
 12 13
 Tính AB , AC , BC , CH .
  Lời giải
Ta có
 AH 2 144
 BH CH AH 2 CH cm
 BH 13
 BC BH CH 13 cm
 652 65
 AB2 BH 2 CH 2 AB cm
 132 13
 2 12
  Ví AdụC 6. C ChoH  C tamB 1 giác44 AABCC vuông12 cm tại B , đường cao BH cm và 4AB 3BC . Tính 
 5
 AB,AC,BC,AH,CH.
  Lời giải
 3
Từ giả thiết ta suy ra AB BC .
 4
 1 1 1
 Mặt khác, ta có . Suy ra
 BH 2 BA2 BC 2
 25 16 1 25
 BC 2 16 BC 4 cm
 144 9BC 2 BC 2 9BC 2
Suy ra BA 3 cm . Từ đây, ta tìm được AC 5 cm, AH 1,8 cm ,
 CH 3,2 cm
 3 Dự án tài tập toán 9. Chương 1: Hệ thức lượng trong tam giác vuông
  Ví dụ 7. Cho hình vuông ABCD có cạnh bằng 2 5 cm. Gọi M, N lần lượt là trung điểm của 
 AD,DC và I là giao điểm của AN,BM và.
 1. Chứng minh rằng AN vuông góc với MB .
 2. Tính AI,MI .
 3. Tính diện tích tứ giác BINC . 
 . Lời giải
1.Xét hai tam giác ADN và BAM
 có Aˆ Dˆ 90 , AD AB , DN AM.
 Suy ra ADN BAM (c g c) , do đó
 D· AN ·ABM . Suy ra
 M· AI ·AMI D· AN ·AMB ·ABM ·AMB 90.
Từ đây, ta có AN  BM .
2. Ta có BM 2 AM 2 AB2 5 20 25 BM 5 cm .
 AM 2
Suy ra MI 1 cm, AI 2 AM 2 MI 2 5 1 4 AI 2 cm .
 MB
 1
3. Ta có S S S (BI.IN BC.CN) 11 cm2 .
 BCNI BCN BIN 2
 12
  Ví dụ 8. Cho tam giác ABC vuông tại A có BC 5 cm , đường cao AH cm . Tính BH,CH.
 5
  Lời giải
 144
Giả sử BH CH . Ta có BH HC BC 5 . Mặt khác BH CH AH 2 . Từ (1) ta có 
 25
(BH CH )2 25 ,
 288 237
suy ra BH 2 2BH.CH CH 2 25 BH 2 CH 2 25 
 25 25
Do đó
 337 288 49
(BH CH )2 BH 2 2BH CH CH 2 . 
 25 25 25
 7
Suy ra BH CH 
 5
Từ (1) và (2) ta có
 4 Dự án tài tập toán 9. Chương 1: Hệ thức lượng trong tam giác vuông
 (BH+CH)+(BH-CH) 16 9
 BH= = cm, CH = BC-BH = cm. 
 2 5 5
  Ví dụ 9. Cho tam giác ABC vuông tại A , đường cao , AkẻH HvuôngM góc với AB
 AB3
 tại M . Chứng minh rằng BM .
 BC 2
  Lời giải
 Trong tam giác vuông AHB
 BH 2
 ta có BM.BA BH 2 , suy ra BM 
 AB
 Mặt khác, trong tam giác vuông ABC , ta có BH.BC AB2 , hay 
 AB2 AB4 AB3
 BH .Do đó BM 
 BC AB.BC 2 BC 2
 Vậy bài toán được chứng minh.
  Ví dụ 10. Cho hình vuông ABCD ,I là điểm thay đổi trên cạnh AB ( I khác A và B ). 
 1 1
 Đường thẳng DI cắt BC tại K . Chứng minh rằng không đổi.
 DI 2 DK 2
  Lời giải
 Qua D kẻ đường thẳng vuông góc với DI , cắt BC tại H . Xét hai tam giác 
 ADI và CDH
 có µA Cµ 90 , AD DC , C· DI C· DH (cùng phụ với góc C· DI) . Suy ra 
 ADI CDH
 (g c g) , do đó DI DH . Suy ra
 1 1 1 1 1
 DI 2 DK 2 DH 2 DK 2 DC 2
 Từ đó, ta có đpcm.
 Ví dụ 11. Cho tam giácABC cân tại A , có góc A nhọn. Vẽ BM
 2
 AM AB 
vuông góc với AC . Chứng minh rằng 2 1
 MC BC 
  Lời giải
 5 Dự án tài tập toán 9. Chương 1: Hệ thức lượng trong tam giác vuông
|Gọi D là điềm đối xứng với C qua A , khi đó AB AD AC nên tam giác BCD vuông tại B và có 
đường cao BM
. Suy ra CM CD BC 2 CM 2AC BC 2 , suy ra
 2
 AC AC AM
 2 1 . Mà AB AC , nên ta có
 BC CM CM
 2
 AB AM
 2 1 .
 BC CM
Vậy bài toán được chứng minh.
 Luyện tập
 Bài 1. Cho tam giác vuông ABC , đường cao AH , cạnh góc vuông AC 60 cm , cạnh huyền 
 BC 100 cm . Tính chu vi tam giác ABC , ABH , ACH.
  Lời giải
Xét tam giác vuông ABC có AB BC 2 AC 2 80 cm .
 AB  AC 6080
 AH 48 cm .
 BC 100
 AB2
 BH 64 cm,CH BC BH 36 cm
 BC
 Chu vi tam giác ABC
 là AB BC CA 240 cm .
 Chu vi tam giác ABH là AB AH HB 192 cm .
 Chu vi tam giác ACH : AC AH HC 144 cm .
 Bài 2. Cho tam giác vuông có các canh góc vuông bằng 5 cm và 12 cm . Tìm cạnh huyền và các 
hình chiếu của các cạnh góc vuông trên cạnh huyền. 
  Lời giải
Các hình chiều của các cạnh lên cạnh huyền là:
 AB2 52 25
 BH cm.
 BC 13 13
 25 144
CH BC CH 13 cm .
 13 13
 Bài 3. Tìm các canh của tam giác vuông, biết đường cao và đường trung tuyền ứng với cạnh huyền 
theo thứ tự là 4cm và 5cm.
  Lời giải
Vì AM là trung tuyến của tam giác ABC vuông tại A nên AM MC MB 5cm , suy ra 
 BC 2MA 10cm.
 6 Dự án tài tập toán 9. Chương 1: Hệ thức lượng trong tam giác vuông
Xét AHM : HM AM 2 AH 2 3 cm . Suy ra 
 BH MB HM 2 cm, HC HM MC 8 cm
Xét tam giác vuông ABC :
 AB2 BH.BC 20 AB 2 5 cm.
 AC 2 CH.CB 80 AC 4 5 cm
 Bài 4. Tìm các cạnh của tam giác vuông, biết đường cao ứmg với cạnh huyền là 4 cm , diện tích 
tam giác vuông bằng 20 cm2 .
  Lời giải
 2S 2.20
Ta có BC ABC 10 cm . 
 AH 4
Đặt BH x(x 0). Ta có
 AH 2 BH.CH 16 x(10 x)
 2 x 2
 x 10x 16 0 
 x 8
Khi BH 2 cm : AB2 BH  BC 2,10 AB 2 5 cm; AC BC 2 AB2 4 5 cm.
Khi BH 8 cm : AB2 BH  BC 810 AB 4 5 cm; AC BC 2 AB2 2 5 cm.
Khi đó ba cạnh của tam giác là 2 5 cm,4 5 cm và 10 cm.
  Bài 5. Cho tam giác ABC vuông tại A , đường cao AH . Biết AH 6 cm và HC HB 9 cm . 
Tính HB, HC.
  Lời giải
Đặt BH x CH 9 x với x 0 .
Ta có
 AH 2 BH  HC x(9 x) 36 x2 9x 36 0
 x 12
 x 3
Vậy HB 3 cm, HC HB 9 12 cm .
 AB 3
 Bài 6. Cho tam giác ABC vuông tại A, , đường cao AH 18 cm . Tính chu vi tam giác 
 AC 4
 ABC.
  Lời giải
Đặt AB 3x AC 4x với x 0 .
 7 Dự án tài tập toán 9. Chương 1: Hệ thức lượng trong tam giác vuông
Suy ra BC AB2 AC 2 5x .
 1 1 1 AB  AC 12x 15
Ta có 2 2 2 AH x cm .
 AH AB AC AB2 AC 2 5 2
Chu vi tam giác ABC
 bằng AB BC CA 12x 90 cm .
 Bài 7. Cho tam giác ABC vuông tại A vái AB AC và đường cao AH.Tính AB, AC biết 
 AH 6 cm và diện tích tam giác ABC bằng 37,5 cm2. 
  Lời giải
Giả sử tam giác đó là ABC có đường cao AH
 2S 237,5
Ta có BC ABC 12,5 cm
 AH 6
Đặt BH x(x 0) . Ta có
 9
 x 
 AH 2 BH.CH 36 x.(12,5 x) x2 12,5x 36 0 2
 x 8
 9 9 15
Khi BH cm : AB2 BH  BC 12,5 AB cm; AC BC 2 AB2 10 cm.
 2 2 2
Khi BH 8 cm : AB2 BH  BC 812,5 AB 10 cm; AC BC 2 AB2 7,5 cm .
Khi đó là ba cạnh của tam giác là AB 7,5 cm, AC 10 cm và BC 12,5 cm .
 Bài 8. Cho hình thang ABCD vuông tại A và D . Hai đường chéo vuông góc với nhau tại O . 
Biết AB 2 13,OA 6 . Tính diện tích hình thang. 
  Lời giải
Xét OAB vuông tại O , ta có:
OB AB2 OA2 (2 13)2 62 4
Xét ABD vuông tại A , đường cao AO ta có: 
 AB2 (2 13)2
 AB2 BD OB BD 13 
 OB 4
 AD BD2 AB2 132 (2 13)2 3 13 .
Ta có OD BD OB 13 4 9 .
 AD2 AD2 (3 13)2
Xét ADC ABC vuông tại D ta có: AD2 OA AC AC 19,5 .
 OA OA 6
 8 Dự án tài tập toán 9. Chương 1: Hệ thức lượng trong tam giác vuông
 OD.AC 9.19,5 9 13
Mà AD.DC OD.AC DC .
 AD 3 13 2
 1
Vậy S AD.(AB DC) 126,75 (đvdt)
 ABCD 2
 Bài 9. Cho tam giác ABC vuông tại A . Đường cao AH , cạnh bên AC 30, HB 32 .Tính độ dài 
 AH, HC, AB
  Lời giải
Đặt HC x(x 0) . Xét ABC vuông tại A , đường cao AH ta có
 AH 2 HC.HB 302 x(x 32)
 (x 18)(x 50) 0
 x 18 
 x 50 
Xét AHC vuông tại H ta có AH AC2 HC2 24 . 
Xét ABC vuông tại A ta có AB2 HB.BC 32.(32 18) 40 .
  Bài 10. Cho hình chữ nhật ABCD có các cạnh AB 60 cm, AD 32 cm . Từ D kẻ đường thẳng 
vuông góc với đường chéo AC . Đường này cắt AC tại E và AB tại F . Tính độ dài các đoạn 
 EA, EC, ED, FB, FD.
  Lời giải
Xét tam giác vuông ADC ta có
 AD2 AD2 322 256
 EA cm
 AC AD2 CD2 322 602 17
 CD2 602 900
 EC cm
 AC 322 602 17
Xét tam giác vuông ADE có
 322.602 480
 tam giác vuông ADE có ED EA.EC cm .
 322 602 17
 AD2 322 544
 FD cm.
 ED 3260 15
 68
 322 682 256
 AF FD2 AD2 322 cm.
 602 15
 256 644
 FB AB AF 60 cm.
 15 15
  Bài 11. Tính diện tích hình thang ABCD , có đường cao bằng 12 cm , hai đường chéo AC
và BD vuông góc với nhau, DB 15 cm .
 9 Dự án tài tập toán 9. Chương 1: Hệ thức lượng trong tam giác vuông
  Lời giải
Qua B vẽ đường thẳng song song với AC , cắt DC ở E . Gọi BH là đường cao của hình thang. Ta 
có BE // AC nên BE  BD.
Áp dụng định lí Pytago vào tam giác vuông BDH , ta có
 BH 2 HD2 BD2 122 HD2 152
 HD2 225 144 81 HD 9 cm
Xét tam giác BDE vuông tại B , ta có
 225
 BD2 DE.DH 152 DE.9 DE 25 cm
 9
Ta có AB CE nên AB CD CE CD DE 25 cm .
 2512
 Do đó S 150 cm2 .
 ABCD 2
 Bài 12. Hình thang cân ABCD có đáy lớn CD 10 cm , đáy nhỏ bằng đường cao, đường chéo 
vuông góc với cạnh bên. Tìm đường cao của hình thang.
  Lời giải
Gọi AH, BK là đường cao của hình thang, Đặt AB AH BK x
 DC AB 10 x
Dễ dàng chứng minh được DH CK .
 2 2
 10 x
Do đó HC .
 2
Xét ADC vuông tại A , ta có AH 2 HD.HC . Do đó
Từ đó suy ra x 2 5 cm . Đường cao của hình thang bằng 2 5 cm .
  Bài 13. Tính diện tích một tam giác vuông có chu vi 72 cm , hiệu giữa đường trung tuyến và 
đường cao ứng với cạnh huyền bằng 7 cm .
  Lời giải
Đặt AM x(x 0) , ta có BC 2x, AH x 7 . Theo các hệ thức trong tam giác vuông
 2 2 2 2
 AB AC BC 4x (1)
 AB.AC BC.AH 2x(x 7) (2)
Từ (1) và (2) suy ra
 AB2 AC 2 2AB.AC 4x2 4x(x 7)
 (AB AC)2 8x2 28x (72 2x)2 8x2 28x
 x2 65x 1296 0 (x 16)(x 81) 0
 x 16 
 x 81 
 10