Kế hoạch bài học Toán hình Lớp 9 - Tiết 23, Bài 3: Liên hệ giữa dây và khoảng cách từ âm đến dây

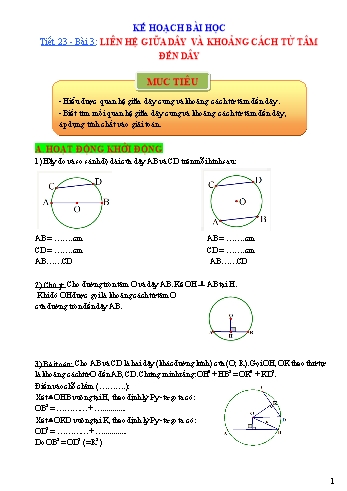
KẾ HOẠCH BÀI HỌC
Tiết 23 - Bài 3: LIÊN HỆ GIỮA DÂY VÀ KHOẢNG CÁCH TỪ TÂM ĐẾN DÂY
- Hiểu được quan hệ giữa dây cung và khoảng cách từ tâm đến dây.
- Biết tìm mối quan hệ giữa dây cung và khoảng cách từ tâm đến dây, 
áp dụng tính chất vào giải toán.
MỤC TIÊU
A. HOẠT ĐỘNG KHỞI ĐỘNG
1) Hãy đo và so sánh độ dài của dây AB và CD trên mỗi hình sau:
AB = ..cm AB = ..cm 
CD = ..cm CD = ..cm
ABCD ABCD
2) Chú ý: Cho đường tròn tâm O và dây AB. Kẻ OH AB tại H.
 Khi đó OH được gọi là khoảng cách từ tâm O 
của đường tròn đến dây AB.
3) Bài toán: Cho AB và CD là hai dây (khác đường kính) của (O; R). Gọi OH, OK theo thứ tự là khoảng cách từ O đến AB, CD. Chứng minh rằng: OH2 + HB2 = OK2 + KD2.
Điền vào chỗ chấm (.):
Xét OHB vuông tại H, theo định lý Py-ta-go ta có:
OB2 =  + ............
Xét OKD vuông tại K, theo định lý Py-ta-go ta có:
OD2 =  + ............
Do OB2 = OD2 (= R2)
Vậy ................... = .
* Chú ý: Bài toán trên còn đúng với hai dây là đường kính hoặc một dây là đư...8cm. Tính khoảng cách giữa hai dây AB và CD.
Bài tập 6: Cho đường tròn (O) và một điểm E nằm ngoài đường tròn, vẽ đường tròn (E) cắt đường tròn (O) tại hai điểm A và B. Các đoạn thẳng EA và EB lần lượt cắt đường tròn (O) tại C và D. Chứng minh rằng hai dây AC và BD của đường tròn (O) bằng nhau.
Gợi ý: Chứng minh OAE = OBE
EO là phân giác góc AEB.
Vậy O cách đều CA và DB
CA = DB
D. HOẠT ĐỘNG VẬN DỤNG 
Bài tập 7: Cho đường tròn (O), điểm A nằm trong đường tròn. Vẽ dây MN vuông góc với OA tại A. Vẽ dây PQ bất kì đi qua A và không vuông góc với OA. Hãy so sánh độ dài hai dây MN và PQ.
Bài tập 8: Cho đường tròn (O) lấy hai dây AM và BN bằng nhau (M và N nằm trên cùng một nửa mặt phẳng bởi là đường thẳng AB). Hai đường thẳng AM và BN cắt nhau tại F. Chứng minh rằng:
OF là phân giác của góc AOB.
OF vuông góc với AB.
E. HOẠT ĐỘNG TÌM TÒI, MỞ RỘNG 
1) Nếu dùng một đoạn vật liệu có cùng độ dài để khép 
kín thành hình tam giác, hình vuông, hình tròn thì hình
 tròn có diện tích lớn nhất. Vì vậy, con người đã dùng 
tính chất này để tạo ra các vật dụng. Dùng tre để làm 
đấu đong, các đồ dùng có dạng hình trụ sẽ đựng được 
nhiều lương thực mà tiết kiệm được vật liệu chế tạo. 
Chế tạo cốc dạng hình trụ sẽ đựng được nhiều chất lỏng hơn.
2) Đố vui? Bạn Minh vẽ một hình thang cân ABCD có tất cả các cạnh tiếp xúc với đường tròn (O) sao cho AB // CD, AB < CD. Giờ ra chơi Minh đố Thông:
Này nhé, rõ ràng khoảng cách từ tâm đường tròn đến các cạnh của hình thang là bằng nhau, theo mối liên hệ giữa dây và khoảng cách từ tâm đến dây thì các cạnh của hình thang phải bằng nhau chứ? Cậu có thấy vô lí không?
Các em hãy giúp Thông giải quyết sai lầm của Minh.
=================================================================