Các bài toán Hình học Lớp 9
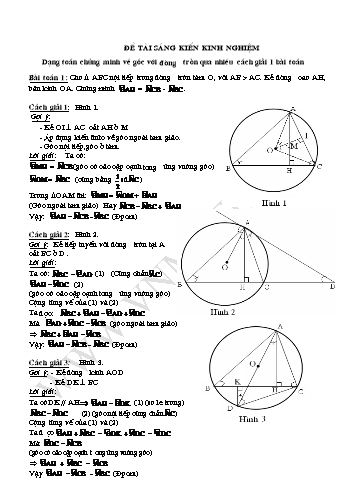
Bài toán 1: Cho D ABC nội tiếp trong đường tròn tâm O, với AB > AC. Kẻ đường cao AH, bán kính OA. Chứng minh = - .
Cách giải 1: Hình 1.
Gợi ý:
- Kẻ OI ^ AC cắt AH ở M
- áp dụng kiến thức về góc ngoài tam giác.
- Góc nội tiếp,góc ở tâm.
Lời giải: Ta có:
= (góc có các cặp cạnh tương ứng vuông góc)
= (cùng bằng sđ)
Trong DOAM thì: = +
(Góc ngoài tam giác) Hay
Vậy: (Đpcm)
Cách giải 2: Hình 2.
Gợi ý: Kẻ tiếp tuyến với đường tròn tại A
cắt BC ở D .
Lời giải:
Ta có: (1) (Cùng chắn)
(2)
(góc có các cặp cạnh tương ứng vuông góc)
Cộng từng vế của (1) và (2)
Ta được:
Mà (góc ngoài tam giác)
ị
Vậy: (Đpcm)
Cách giải 3: Hình 3.
Gợi ý: - Kẻ đường kính AOD
- Kẻ DK ^ BC
Lời giải:
Ta cóDK // AH (1) (so le trong)
(2) (góc nội tiếp cùng chắn)
Cộng từng vế của (1) và (2)
Ta được
Mà:
(góc có các cặp cạnh tương ứng vuông góc)
ị
Vậy (Đpcm)
Tóm tắt nội dung tài liệu: Các bài toán Hình học Lớp 9
Đề tài sáng kiến kinh nghiệm Dạng toán chứng minh về góc với đường tròn qua nhiều cách giải 1 bài toán Bài toán 1: Cho D ABC nội tiếp trong đường tròn tâm O, với AB > AC. Kẻ đường cao AH, bán kính OA. Chứng minh = - . Cách giải 1: Hình 1. Gợi ý: - Kẻ OI ^ AC cắt AH ở M - áp dụng kiến thức về góc ngoài tam giác. - Góc nội tiếp,góc ở tâm. Lời giải: Ta có: = (góc có các cặp cạnh tương ứng vuông góc) = (cùng bằng sđ) Trong DOAM thì: = + (Góc ngoài tam giác) Hay Vậy: (Đpcm) Cách giải 2: Hình 2. Gợi ý: Kẻ tiếp tuyến với đường tròn tại A cắt BC ở D . Lời giải: Ta có: (1) (Cùng chắn) (2) (góc có các cặp cạnh tương ứng vuông góc) Cộng từng vế của (1) và (2) Ta được: Mà (góc ngoài tam giác) ị Vậy: (Đpcm) Cách giải 3: Hình 3. Gợi ý: - Kẻ đường kính AOD - Kẻ DK ^ BC Lời giải: Ta cóDK // AH (1) (so le trong) (2) (góc nội tiếp cùng chắn) Cộng từng vế của (1) và (2) Ta được Mà: (góc có các cặp cạnh tương ứng vuông góc) ị Vậy (Đpcm) Cá... đó: ^P1=^P2 APK = API ( Có chung cạnh huyền và một cặp góc nhọn bằng nhau ) PK = PI Cách giải 2: Hình 2 Gợi ý: - Ngoài cách chứng minh hai tam giác APK và API bằng nhau cách 1 ta chứng minh^P1=^P2. Ta chứng minh ^A1=^A2 - Gọi F là giao điểm của AP với đường tròn đường kính AD Lời giải: Ta có: = 900 ( Góc nội tiếp chắn nữa đường tròn) Tam giác ADP cân tại D có DF là đường cao nên DF cũng là phân giác suy ra: ^D1=^D2 mà^A1=^D2 ;^D1=^A2Vì đều là góc có các cặp cạnh tương ứng vuông góc Suy ra: ^A1=^A2 APK = API ( Có chung cạnh huyền và một cặp góc nhọn bằng nhau ) PK = PI Cách giải 3: Hình 2. Gợi ý: - Cách giải này chúng ta cũng đi chứng minh nhưng việc chứng minh được áp dụng bằng kiến thức khác. - Chú ý rằng AB là tiếp tuyến của đường tròn tâm D nên ta có: Lời giải: Ta có ( Có số đo bằng sđ ) Mặt khác góc là góc tạo bởi tiếp tuyến và dây cung AP của đường tròn tâm D nên góc bằng số đo của góc ở tâm cùng chắn một cung là góc ^ = Suy ra: ^A1=^A2 APK = API ( Có chung cạnh huyền và một cặp góc nhọn bằng nhau ) PK = PI Cách giải 4: Hình 3 Gợi ý: - Kéo dài K cắt đường tròn tâm D tại E - áp dụng định lí của góc tạo bởi tiếp tuyến và dây cung Lời giải: DK AE nên . Góc (góc tạo bởi tiếp tuyến và dây cung )Vì AP lại đi qua điểm chính giữa của cung AE nên AP là tia phân giác của góc Suy ra: ^A1=^A2 APK = API ( Có chung cạnh huyền và một cặp góc nhọn bằng nhau ) PK = PI Đối với bài toán trên để chứng minh hai đoạn thẳng PK và PI bằng nhau ta đi chứng minh APK = API vấn đề giáo viên cần cho học sinh tư duy và vận dụng sáng tạo kiến thức về : - Trường hợp bằng nhau trong tam giác vuông - Góc tạo bởi tiếp tuyến và dây cung. - Góc nội tiếp Dạng bài có quan hệ liên kết nhau khi phát triển một bài đơn giản đến phức tạp Bài toán 3: Cho tam giác ABC, về phía ngoài tam giác, dựng các tam giác đều ABF; ACD; BCE. Chứng minh rằng AE; BD; CF đồng quy. Bài giải: Gọi O là giao điểm của BD và CF. Ta cần ch...à một bài toán hình tương đối khó đối với học sinh nếu không có tư duy tốt trong hình học. Khi đưa ra bài toán này ngay cả việc vẽ hình cũng là một vấn đề khó và các em đã không tìm ra được lời giải. Dưới sự hướng dẫn của thầy. Ta có AN; BP và AN là các tia phân giác của tam giác ABC. Gọi I là giao điểm của các đường phân giác. Khi đó ta có I chính là tâm của đường tròn nội tiếp tam giác ABC Để chứng minh cho RS // BC và I RS ta đi chứng minh IR // BC ; IS // BC rồi sử dụng tiên đề về đường thẳng song song để suy ra điều phải chứng minh. Sau một thời gian ngắn một học sinh đã tìm ra được lời giải cho bài toán này. Và cũng là lời giải ngắn mà thầy đã tìm ra. Lời giải: Xét NBI ta có: mà (Góc nội tiếp chắn cung ) = do đó ; = ( Góc ngoài của tam giác ABI ) Suy ra : NBI cân tại N N thuộc trung trực của đoạn thẳng BI Ta chứng minh đường trung trực của đoạn thẳng này chính là RN. Gọi H là giao điểm của MN và PB. Ta có =sđ = Vì là góc có đỉnh nằm bên trong đường tròn và ; ; = 3600 = 900 RN là trung trực của đoạn thẳng BI BR = RI RBI cân tại R IR // BC ( Vì tạo với các tuyến BI hai góc so le trong bằng nhau ) Cũng chứng minh tương tự ta được IS // BC, từ điểm I ở ngoài đường thẳng BC ta chỉ có thể kẻ được một đường thẳng song song với BC R ; I ; S thẳng hàng. Vậy RS // BC và RS đi qua tâm I của đường tròn nội tiếp tam giác ABC ( Đpcm) Cách giải 2: Hình 2 Gợi ý: Trong cách giải này yêu cầu học sinh phải nắm lại kiến thức cũ về Tính chất đường phân giác trong tam giác đây là tính chất quan trọng mà các em đã được học ở lớp 8 đa số học sinh ít thậm trí là không hay để ý đến tính chất này. Lời giải: Theo giả thiết ta có do đó MN là phân giác của góc áp dụng tính chất đường phân giác trong tam giác ABN ta có: ( 1) Tương tự: NP là phân giác của tam giác ACN (2) vì nên BN = CN kết hợp với (1) và (2) ta được RS // BC Gọi giao điểm của RS với AN là I, của BC và AN là D vì RS // BC nên ta có: mà
File đính kèm:
 cac_bai_toan_hinh_hoc_lop_9.doc
cac_bai_toan_hinh_hoc_lop_9.doc

