Đề thi giữa kỳ II môn Toán Lớp 10 - Tổ 2 - Năm học 2020-2021 (Có đáp án)

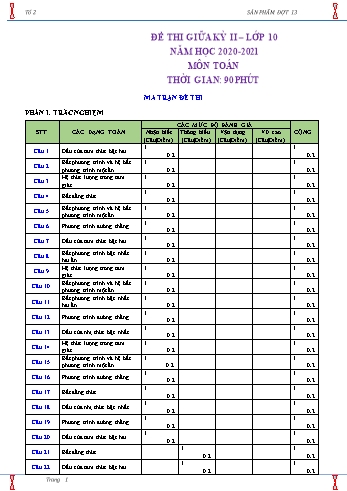
 Tổ 2 SẢN PHẨM ĐỢT 13
 ĐỀ THI GIỮA KỲ II – LỚP 10
 NĂM HỌC 2020-2021
 MÔN TOÁN
 THỜI GIAN: 90 PHÚT
 MA TRẬN ĐỀ THI
PHẦN I. TRẮC NGHIỆM
 CÁC MỨC ĐỘ ĐÁNH GIÁ
 STT CÁC DẠNG TOÁN Nhận biết Thông hiểu Vận dụng VD cao CỘNG
 (Câu|Điểm) (Câu|Điểm) (Câu|Điểm) (Câu|Điểm)
 1 1
 Câu 1 Dấu của tam thức bậc hai
 0.2 0.2
 Bất phương trình và hệ bất 1 1
 Câu 2
 phương trình một ẩn 0.2 0.2
 Hệ thức lượng trong tam 1 1
 Câu 3
 giác 0.2 0.2
 1 1
 Câu 4 Bất đẳng thức
 0.2 0.2
 Bất phương trình và hệ bất 1 1
 Câu 5
 phương trình một ẩn 0.2 0.2
 1 1
 Câu 6 Phương trình đường thẳng
 0.2 0.2
 1 1
 Câu 7 Dấu của tam thức bậc hai
 0.2 0.2
 Bất phương trình bậc nhất 1 1
 Câu 8
 hai ẩn 0.2 0.2
 Hệ thức lượng trong tam 1 1
 Câu 9
 giác 0.2 0.2
 Bất phương trình và hệ bất 1 1
 Câu 10
 phương trình một ẩn 0.2 0.2
 Bất phương trình bậc nhất 1 1
 Câu 11
 hai ẩn 0.2 0.2
 1 1
 Câu 12 Phương trình đường thẳng
 0.2 0.2
 1 1
 Câu 13 Dấu của nhị thức bậc nhất
 0.2 0.2
 Hệ thức lượng trong tam 1 1
 Câu 14
 giác 0.2 0.2
 Bất phương trình và hệ bất 1 1
 Câu 15
 phương trình một ẩn 0.2 0.2
 1 1
 Câu 16 Phương trình đường thẳng
 0.2 0.2
 1 1
 Câu 17 Bất đẳng thức
 0.2 0.2
 1 1
 Câu 18 Dấu của nhị thức bậc nhất
 0.2 0.2
 1 1
 Câu 19 Phương trình đường thẳng
 0.2 0.2
 1 1
 Câu 20 Dấu của tam thức bậc hai
 0.2 0.2
 1 1
 Câu 21 Bất đẳng thức
 0.2 0.2
 1 1
 Câu 22 Dấu của tam thức bậc hai
 0.2 0.2
 Trang 1 Tổ 2 SẢN PHẨM ĐỢT 13
 1 1
 Câu 23 Dấu của nhị thức bậc nhất
 0.2 0.2
 Hệ thức lượng trong tam 1 1
 Câu 24
 giác 0.2 0.2
 Bất phương trình bậc nhất 1 1
 Câu 25
 hai ẩn 0.2 0.2
 1 1
 Câu 26 Dấu của nhị thức bậc nhất
 0.2 0.2
 1 1
 Câu 27 Phương trình đường thẳng
 0.2 0.2
 1 1
 Câu 28 Phương trình đường thẳng
 0.2 0.2
 Bất phương trình và hệ bất 1 1
 Câu 29
 phương trình một ẩn 0.2 0.2
 1 1
 Câu 30 Phương trình đường thẳng
 0.2 0.2
 1 1
 Câu 31 Dấu của tam thức bậc hai
 0.2 0.2
 Bất phương trình và hệ bất 1 1
 Câu 32
 phương trình một ẩn 0.2 0.2
 1 1
 Câu 33 Bất đẳng thức
 0.2 0.2
 1 1
 Câu 34 Dấu của tam thức bậc hai 
 0.2 0.2
 Hệ thức lượng trong tam 1 1
 Câu 35
 giác 0.2 0.2
 20 15 35
 TỔNG CỘNG
 4.0 3.0 7.0
PHẦN II: TỰ LUẬN
Bài 1: (1 điểm) Hệ thức lượng trong tam giác.
Bài 2: (1 điểm) Dấu nhị thức bậc nhất.
Bài 3: (0,5 điểm) Phương trình đường thẳng.
Bài 4: (0,5 điểm) Dấu của tam thức bậc hai.
 ĐỀ THI
PHẦN I: TRẮC NGHIỆM (7 ĐIỂM)
Câu 1. [NB] Với x thuộc tập hợp nào dưới đây thì f x x2 2x 3 luôn dương?
 A.  B. ¡
 C. ; 1  3; D. 1;3 
 2x 1
 x 1
 3
Câu 2. [ NB ]Tập nghiệm của hệ bất phương trình là
 4 3x
 3 x
 2
 4 4 3 1 
 A. 2; . B. 2; . C. 2; . D. 1; .
 5 5 5 3 
Câu 3. [ NB ] Tam giác ABC có AC 3 3 , AB 3, BC 6. Tính số đo góc B
 A. 60. B. 45. C. 30. D. 120.
Câu 4. [NB] Tìm mệnh đề đúng trong các mệnh đề sau:
 Trang 2 Tổ 2 SẢN PHẨM ĐỢT 13
 1 1
 A. a b . B. a b ac bc.
 a b
 a b 0 a b
 C. ac bd. D. a.c b.d.
 c d 0 c d
Câu 5. [NB] Số x 3 là nghiệm của bất phương trình nào sau đây?
 A. 5 x 1. B. 3x 1 4 . C. 4x 11 x . D. 2x 1 3 .
Câu 6. [NB] Đường thẳng đi qua A 1; 2 , nhận n (2; 4) làm véctơ pháp tuyến có phương trình 
 là:
 A. x – 2y – 4 0 .B. x y 4 0 .
 C. – x 2y – 4 0 . D. x – 2y 5 0 .
Câu 7. [ NB] Khẳng định nào sau đây là đúng về dấu của tam thức bậc hai f x x 2 2x 1.
 A. f x 0,x ¡ \ 1.
 B. f x 0,x ¡ .
 C. f x 0,x 1; và f x 0,x ; 1 .
 D. f x 0,x ¡ \ 1.
Câu 8. [NB] Trong các cặp số x; y , đâu là một nghiệm của bất phương trình bậc nhất hai ẩn 
 2x 3y 2 .
 A. x; y 1;0 . B. x; y 0;0 .C. x; y 0;1 . D. x; y 1; 1 .
Câu 9. [ NB] Cho tam giác ABC tùy ý có BC a,CA b, AB c , khẳng định nào sau đây đúng?
 A. a2 b2 c2 2bc cos A. B. a2 b2 c2 2bc cos A.
 C. a2 b2 c2 . D. a2 b2 c2 2bcsin A .
Câu 10. [ NB] Điều kiện để bất phương trình ax b 0 vô nghiệm là:
 a 0 a 0
 A. . B. .
 b 0 b 0
 a 0 a 0
 C. . D. .
 b 0 b 0
Câu 11. [NB] Cho các bất phương trình sau, đâu không phải là bất phương trình bậc nhất hai ẩn?
 3 y
 A. x 0 .B. .C. .D. . x y 1 3x z 0 x 6 0
 y 2
 x 5 t
Câu 12. [NB] Cho phương trình tham số của đường thẳng d : . Trong các phương trình sau, 
 y 9 2t
 phương trình nào là phương trình tổng quát của d ?
 A. 2x y 1 0 . B. .2 x C.3y . 1 0D. . x 2y 2 0 x 2y 2 0
Câu 13 . [NB] Nhị thức 2x 3 nhận giá trị dương khi và chỉ khi 
 3 2 3 2
 A. .x B. . x C. . D. .x x 
 2 3 2 3
 Trang 3 Tổ 2 SẢN PHẨM ĐỢT 13
Câu 14 . [NB] Cho tam giác ABC có Bµ 120 , cạnh AC 2 3 cm . Bán kính R của đường tròn ngoại 
 tiếp tam giác ABC bằng
 A. .RB. .C.2 c .mD. . R 4 cm R 1cm R 3 cm
Câu 15. [NB] Tập nghiệm của bất phương trình 12 5x x là:
 A. 3; . B. . ;3 C. . D.;2 . 2; 
Câu 16. [NB] Trong mặt phẳng tọa độ Oxy , một vectơ chỉ phương của đường thẳng d có phương trình 
 x 1 2t
 ,t R là:
 y 5 4t
 A. 2;4 . B. . 4; 2 C. . 1; 2 D. . 1;2 
Câu 17. [NB] Cho bất đẳng thức a b a b . Dấu đẳng thức xảy ra khi nào?
 A. .a b B. . ab 0 C. ab 0 D. . a b
Câu 18. [NB] Cho nhị thức bậc nhất f x 23x 20 . Khẳng định nào sau đây đúng?
 20 
 A. f x 0 với . x ¡ B. f với x . 0 x ; 
 23 
 23 20 
 C. f x 0 với .x D. f với x . 0 x ; 
 20 23 
Câu 19. [NB] Trong mặt phẳng tọa độ Oxy , cho đường thẳng d : 2x 3y 4 0 . Véctơ nào sau đây là 
 một véctơ pháp tuyến của đường thẳng d ?
     
 A. n 3;2 . B. n 4; 6 . C. n 2; 3 . D. n 2;3 .
 1 1 1 1 
Câu 20. [NB] Cho tam thức f x ax2 bx c a 0 , b2 4ac . Ta có f x 0 với x ¡ khi 
 và chỉ khi
 a 0 a 0 a 0 a 0
 A. . B. .C. .D. .
 0 0 0 0
Câu 21. [TH] Cho a,b ¡ ;a,b 0 và a.b2 4 . Giá trị nhỏ nhất của biểu thức S a b là:
 A. 0 . B. 2 . C. 1. D. 3 .
Câu 22. [TH] Bảng xét dấu sau là bảng xét dấu của biểu thức nào?
 x – 3 1 2 
 f (x) – 0 + 0 – 0 +
 (x2 2x 3)
 A. f (x) (x2 2x 3)(2 x) . B. f (x) .
 (x 2)
 (2 x)
 C. f (x) (x2 2x 3)(x 2) . D. f (x) .
 (x2 2x 3)
 2x 3 x 1 
Câu 23. [TH] Cho biểu thức f x . Số các giá trị nguyên dương của x để f x 0 là:
 x 7
 A. 1. B. 6. C. 5. D. Vô số.
Câu 24. [TH] Cho tam giác ABC có AB 9, AC 18 và A 60. Bán kính R của đường tròn ngoại 
 tiếp tam giác ABC là:
 Trang 4 Tổ 2 SẢN PHẨM ĐỢT 13
 A. 3 . B. 9 3 . C. 9 . D. 6 .
Câu 25. [TH] Điểm nào sau đây thuộc miền nghiệm của bất phương trình 2x y 3 0 ?
 A. 1; 2 . B. 0;4 .C. 2;0 .D. 1;2 .
 x2
Câu 26. [TH] Có bao nhiêu số nguyên để bất phương trình x 1 có nghiệm ?
 x 2
 A. 4 .B. 5 .C. 3 .D. 2 .
Câu 27. [TH] Trong mặt phẳng Oxy cho đường thẳng :2x y 3 0 . Viết phương trình đường 
 thẳng d / / và đi qua điểm M 1;4 . 
 A. x 2y 7 0.B. x 2 y 6 0 . C. 2x y 6 0 . D. 2x y 6 0 .
 x 1 m.t
Câu 28. [TH] Trong mặt phẳng Oxy cho hai đường thẳng d :2x y 3 0 và d ': . 
 y 2 m 1 .t
 Giá trị của m thuộc khoảng nào để d  d ' .
 A. m 3;2 . B. m 6; 1 . C. m 2;6 . D. m 1;5 .
 ì
 ï 2x - 1 £ 7
 ï
Câu 29. [NB] Hệ phương trình sau có bao nhiêu nghiệm nguyên í x 3x + 1
 ï - £ 2x + 4
 îï 2 5
 A. 5. B. 6 . C. 7 . D. 8
Câu 30. [NB] Trong mp (Oxy) cho 2 điểm A(- 3;5) và B(2;7). Điểm nào sau đây thuộc đường thẳng 
 trung trực cạnh AB
 æ3 ö æ 5ö æ 1 ö
 A. M ç ;1÷. B. N ç1; ÷. C. P (0;- 1). D. Qç- ;4÷
 èç2 ø÷ èç 2ø÷ èç 2 ø÷
Câu 31. [TH] Tổng bình phương các giá trị nguyên của tham số m để phương trình 
 m 2 x2 2 m 2 x 3 0 vô nghiệm là
 A.1. B. 5 . C. 4 . D. 3 .
 x2 5x 4 0
Câu 32. [TH] Tìm tất cả các giá trị của tham số m để hệ bất phương trình có nghiệm.
 x m 0
 A. m 1. B. 1 m 4 . C. m 4 . D. m 4 .
Câu 33. [TH] Cho tam giác ABC có diện tích S , các cạnh BC a, AC b, AB c . Giá trị nhỏ nhất 
 a2 b2 c2
 của biểu thức Q bằng: 
 S
 A. 3 5 .B. 5 2 .C. 4 3 .D. 6 2 .
Câu 34. [TH] Giá trị nguyên nhỏ nhất của tham số m để hàm số 
 f x m 4 x2 m 4 x 2m 1 xác định với mọi x ¡ là: 
 A. 3 .B. 2 .C. 0 .D. 4 .
Câu 35. [TH] Tính số đo góc B của tam giác ABC có các cạnh BC a, AC b, AB c thỏa mãn: 
 a4 b4 c4 a2c2 2a2b2 2b2c2 0 .
 A. 300 .B. 300 hoặc1500 .C. 600 . D. 600 hoặc1200 .
PHẦN II: TỰ LUẬN (3 ĐIỂM)
 Trang 5 Tổ 2 SẢN PHẨM ĐỢT 13
Bài 1. [ VD] Cho ABC có µA 900 , bán kính đường tròn ngoại tiếp R 7 và bán kính đường tròn 
 nội tiếp r 3. Tính diện tích tam giác.
Bài 2. [ VD] Tìm m để hàm số f x x 1 x 2 m luôn dương x ¡ .
Bài 3. [VDC] Trong mặt phẳng toạ độ Oxy , cho hình chữ nhật ABCD có diện tích là 24 , các đường 
 thẳng AB, BC, CD, DA lần lượt đi qua các điểm M 3;1 , N 7; 1 , P 9;2 , Q 4;3 . Viết 
 phương trình đường thẳng AB .
 6y2 y m2
Bài 4: [VDC] Cho f x 2021x2 4xy x . Tìm mđể f x 0 x, y
 2021 2021 2021
 --------- HẾT--------
 Trang 6 Tổ 2 SẢN PHẨM ĐỢT 13
 HƯỚNG DẪN GIẢI
PHẦN I: TRẮC NGHIỆM
 BẢNG ĐÁP ÁN
 1.D 2.A 3.A 4.D 5.D 6.D 7.A 8.C 9.A 10.C
 11.A 12.A 13.A 14.A 15.C 16.C 17.C 18.D 19.B 20.A
 21.D 22.C 23.C 24.C 25.A 26.A 27.D 28.D 29.C 30.A
 31.B 32.D 33.C 34.B 35.D
Câu 1. [NB] Với x thuộc tập hợp nào dưới đây thì f x x2 2x 3 luôn dương?
 A.  B. ¡
 C. ; 1  3; D. 1;3 
 Lời giải
 Yêu cầu cần đạt: Nhận biết được định lý dấu tam thức bậc hai
 2 x 1
 +) Ta có : f x x 2x 3 0 
 x 3
 +) Mà a 1 0 nên bảng xét dấu của f x x2 2x 3 như sau: 
 +) Vậy f x x2 2x 3luôn dương khi và chỉ khi x 1;3 .
 2x 1
 x 1
 3
Câu 2. [ NB ]Tập nghiệm của hệ bất phương trình là
 4 3x
 3 x
 2
 4 4 3 1 
 A. 2; . B. 2; . C. 2; . D. 1; .
 5 5 5 3 
 Lời giải
 Yêu cầu cần đạt: giải được bất phương trình bậc nhất 1 ẩn.
 2x 1
 x 1 4
 3 2x 1 3x 3 5x 4 x 4 
 5 x 2; .
 4 3x 4 3x 6 2x x 2 5 
 3 x x 2
 2
Câu 3. [ NB ] Tam giác ABC có AC 3 3 , AB 3, BC 6. Tính số đo góc B
 Trang 7 Tổ 2 SẢN PHẨM ĐỢT 13
 A. 60. B. 45. C. 30. D. 120.
 Lời giải
 Yêu cầu cần đạt: nhận biết được định lý côsin
 2
 2 2
 AB2 BC 2 AC 2 3 6 3 3 1
 cos B Bµ 60
 2AB.BC 2.3.6 2
Câu 4. [NB] Tìm mệnh đề đúng trong các mệnh đề sau:
 1 1
 A. a b . B. a b ac bc.
 a b
 a b 0 a b
 C. ac bd. D. a.c b.d.
 c d 0 c d
 Lời giải
 Yêu cầu cần đạt: Nhận biết được tính chất của bất đẳng thức
 1 1
 A sai vì thiếu đk 0 a b , B sai vì thiếu đk c 0 ,
 a b
 0 a b
 C sai vì thiếu đk ac bd
 0 c d
Câu 5. [NB] Số x 3 là nghiệm của bất phương trình nào sau đây?
 A. 5 x 1. B. 3x 1 4 . C. 4x 11 x . D. 2x 1 3 .
 Lời giải
 Yêu cầu cần đạt: Nhận biết được nghiệm của bất phương trình bậc nhất một ẩn
 Thay x 3 vào các bất phương trình ta có phương án D đúng.
Câu 6. [NB] Đường thẳng đi qua A 1; 2 , nhận n (2; 4) làm véctơ pháp tuyến có phương trình 
 là:
 A. x – 2y – 4 0 .B. x y 4 0 .
 C. – x 2y – 4 0 . D. x – 2y 5 0 .
 Lời giải
 Yêu cầu cần đạt: Viết được phương trình tổng quát của đường thẳng
 Đường thẳng đi qua A 1; 2 , nhận n (2; 4) làm véctơ pháp tuyến có phương trình là:
 2 x 1 4 y 2 0 x 2y 5 0.
Câu 7. [ NB] Khẳng định nào sau đây là đúng về dấu của tam thức bậc hai f x x 2 2x 1.
 A. f x 0,x ¡ \ 1.
 B. f x 0,x ¡ .
 C. f x 0,x 1; và f x 0,x ; 1 .
 D. f x 0,x ¡ \ 1.
 Trang 8 Tổ 2 SẢN PHẨM ĐỢT 13
 Lời giải
 Yêu cầu cần đạt: Nhận biết được dấu của tam thức bậc hai cụ thể.
Câu 8. [NB] Trong các cặp số x; y , đâu là một nghiệm của bất phương trình bậc nhất hai ẩn 
 2x 3y 2 .
 A. x; y 1;0 . B. x; y 0;0 .C. x; y 0;1 . D. x; y 1; 1 .
 Lời giải
 Yêu cầu cần đạt: Nhận biết được một bộ số là nghiệm của bất phương trình bậc nhất hai ẩn.
 Thay lần lượt các cặp số x; y , ta nhận thấy ở đáp án C có 2.0 3.1 2 là một mệnh đề đúng 
 nên x; y 0;1 là một nghiệm.
Câu 9. [ NB] Cho tam giác ABC tùy ýcó BC a,CA b, AB c , khẳng định nào sau đây đúng?
 A. a2 b2 c2 2bc cos A. B. a2 b2 c2 2bc cos A.
 C. a2 b2 c2 . D. a2 b2 c2 2bcsin A .
 Lời giải
 Yêu cầu cần đạt: Nhận biết được định lý cosin trong tam giác
 Theo địnhlýcô sin trong tam giác ta có a2 b2 c2 2bc cos A
Câu 10. [ NB] Điều kiện để bất phương trình ax b 0 vô nghiệm là:
 a 0 a 0
 A. . B. .
 b 0 b 0
 a 0 a 0
 C. . D. .
 b 0 b 0
 Lời giải
 Yêu cầu cần đạt: Nhận biết được điều kiện có nghiệm, vô nghiệm của bất phương trình bậc 
 nhất một ẩn
 a 0
 Điều kiện để bất phương trình đã cho vô nghiệm là 
 b 0
Câu 11. [NB] Cho các bất phương trình sau, đâu không phải là bất phương trình bậc nhất hai ẩn?
 3 y
 A. x 0 .B. x y 1.C. 3x z 0 .D. x 6 0.
 y 2
 Lời giải
 Yêu cầu cần đat: Nhận biết được dạng của bất phương trình bậc nhất hai ẩn
 Bất phương trình bậc nhất hai ẩn có dạng: ax by c (hoặc ax by 0, ax by 0,
 ax by 0) với a,b,c ¡ , a và b không đồng thời bằng 0.
 x 5 t
Câu 12. [NB] Cho phương trình tham số của đường thẳng d : . Trong các phương trình sau, 
 y 9 2t
 phương trình nào là phương trình tổng quát của d ?
 A. 2x y 1 0 . B. 2x 3y 1 0 . C. x 2y 2 0 . D. x 2y 2 0 .
 Trang 9 Tổ 2 SẢN PHẨM ĐỢT 13
 Lời giải
 Yêu cầu cần đat: Chuyển phương trình tham số của đường thẳng sang phương trình tổng quát
 x 5 t y 9
 Ta có: d : x 5 2x y 1 0 .
 y 9 2t 2
Câu 13 . [NB] Nhị thức 2x 3 nhận giá trị dương khi và chỉ khi 
 3 2 3 2
 A. x . B. x . C. x . D. x .
 2 3 2 3
 Lời giải
 Yêu cầu cần đạt: Nhận biết được dấu của nhị thức bậc nhất
 3
 Ta có 2x 3 0 x .
 2
Câu 14 . [NB] Cho tam giác ABC có Bµ 120 , cạnh AC 2 3 cm . Bán kính R của đường tròn ngoại 
 tiếp tam giác ABC bằng
 A. R 2 cm .B. R 4 cm .C. R 1cm .D. R 3 cm .
 Lời giải
 Yêu cầu cần đạt: Áp dụng công thức định lí sin tính bán kính đường tròn ngoại tiếp
 Áp dụng định lý sin trong tam giác có: 
 AC AC 2 3
 2R R 2 cm .
 sin B 2sin B 2sin120
Câu 15. [NB] Tập nghiệm của bất phương trình 12 5x x là:
 A. 3; . B. ;3 . C. ;2 . D. 2; .
 Lời giải
 Yêu cầu cần đạt : nhận biết được cách giải bất phương trình một ẩn.
 Ta có 12 5x x 12 6x 2 x . 
 Vậy tập nghiệm của bất phương trình là S ;2 .
Câu 16. [NB] Trong mặt phẳng tọa độ Oxy , một vectơ chỉ phương của đường thẳng d có phương trình 
 x 1 2t
 ,t R là:
 y 5 4t
 A. 2;4 . B. 4; 2 . C. 1; 2 . D. 1;2 .
 Lời giải
 Yêu cầu cần đạt : nhận biết được vectơ chỉ phương của đường thẳng.
 Trang 10