Đề kiểm tra định kì học kì I môn Toán Lớp 10 - Năm học 2020-2021 (Có đáp án)

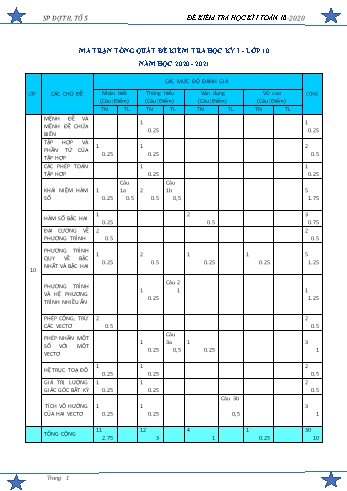
 SP ĐỢT 8, TỔ 5 ĐỀ KIỂM TRA HỌC KÌ I TOÁN 10-2020 
 MA TRẬN TỔNG QUÁT ĐỀ KIỂM TRA HỌC KỲ I - LỚP 10
 NĂM HỌC 2020 - 2021
 CÁC MỨC ĐỘ ĐÁNH GIÁ
LỚP CÁC CHỦ ĐỀ Nhận biết Thông hiểu Vận dụng VD cao CỘNG
 (Câu|Điểm) (Câu|Điểm) (Câu|Điểm) (Câu|Điểm)
 TN TL TN TL TN TL TN TL
 MỆNH ĐỀ VÀ 
 1 1
 MỆNH ĐỀ CHỨA 
 0.25 0.25
 BIẾN
 TẬP HỢP VÀ 
 1 1 2
 PHẦN TỬ CỦA 
 0.25 0.25 0.5
 TẬP HỢP
 CÁC PHÉP TOÁN 1 1
 TẬP HỢP 0.25 0.25
 Câu Câu 
 KHÁI NIỆM HÀM 1 1a 2 1b 5
 SỐ 0.25 0.5 0.5 0,5 1.75
 1 2 3
 HÀM SỐ BẬC HAI
 0.25 0.5 0.75
 ĐẠI CƯƠNG VỀ 2 2
 PHƯƠNG TRÌNH 0.5 0.5
 PHƯƠNG TRÌNH 
 1 2 1 1 5
 QUY VỀ BẬC 
 0.25 0.5 0.25 0.25 1.25
 NHẤT VÀ BẬC HAI
10
 Câu 2
 PHƯƠNG TRÌNH 
 1 1 1
 VÀ HỆ PHƯƠNG 
 0.25 1.25
 TRÌNH NHIỀU ẨN
 PHÉP CỘNG, TRỪ 2 2
 CÁC VECTƠ 0.5 0.5
 Câu 
 PHÉP NHÂN MỘT 
 1 3a 1 3
 SỐ VỚI MỘT 
 0.25 0,5 0.25 1
 VECTƠ
 1 1 2
 HỆ TRỤC TOẠ ĐỘ
 0.25 0.25 0,5
 GIÁ TRỊ LƯỢNG 1 1 2
 GIÁC GÓC BẤT KỲ 0.25 0.25 0.5
 Câu 3b
 TÍCH VÔ HƯỚNG 1 1 3
 CỦA HAI VECTƠ 0.25 0.25 0,5 1
 11 12 4 1 30
 TỔNG CỘNG
 2.75 3 1 0.25 10
 Trang 1 SP ĐỢT 8, TỔ 5 ĐỀ KIỂM TRA HỌC KÌ I TOÁN 10-2020 
 MA TRẬN CHI TIẾT ĐỀ KIỂM TRA ĐỊNH KỲ - HỌC KỲ I - LỚP 10
 NĂM HỌC 2020 - 2021
  TRẮC NGHIỆM: 70%
 CÁC MỨC ĐỘ ĐÁNH GIÁ CỘNG
 CÁC DẠNG TOÁN Nhận biết Thông hiểu Vận dụng VD cao
 (Câu|Điểm)
 (Câu|STT) (Câu|STT) (Câu|STT) (Câu|STT)
 1 1
Phủ định của một mệnh đề
 c12 0.25
Tập hợp con - Hai tập hợp bằng 1 1 2
nhau c1 c13 0.5
Tổng hợp từ 3 loại phép toán tập 1 1
hợp. c14 0.25
 1 1
Tìm tập xác định của hàm số
 c2 0.25
Tính đồng biến, nghịch biến của 1 1
hàm số c15 0.25
Tính chẵn, lẻ của hàm số không 1 1
tham số c16 0.25
 1 1
Tọa độ đỉnh, trục đối xứng 
 c3 0.25
 1 1
Xác định hàm số bậc hai 
 c24 0.25
Min-Max, tập giá trị liên quan hàm 1 1
bậc 2 c25 0.25
 1 1
Tìm điều kiện của phương trình
 c4 0.25
Hai phương trình tương đương, hệ 1 1
quả c5 0.25
ĐK phương trình bậc nhất có 
 1 1
nghiệm duy nhất, vô nghiệm, có 
 c6 0.25
nghiệm, vô số nghiệm
ĐK để PT bậc 2 có nghiệm, vô 1 1
nghiệm, 2 nghiệm pb c26 0.25
 1 1
Phương trình chứa dấu GTTĐ
 c17 0.25
PP biến đổi tương đương GPT Vô 1 1
tỷ c18 0.25
GPT Vô tỷ bằng PP hàm số, đánh 1 1
giá đánh giá c28 0.25
 1 1
Hệ phương trình bậc nhất hai ẩn
 c19 0.25
 1 1
Chứng minh đẳng thức vectơ
 c7 0.25
 1 1
Tính độ dài vectơ tổng, hiệu
 c8 0.25
Phân tích 1 vectơ theo hai vectơ 1 1
không cùng phương c20 0.25
Tìm tập hợp điểm thoả điều kiện 1 1
cho trước c27 0.25
Xác định toạ độ vectơ thoả mãn 1 1
điều kiện cho trước c9 0.25
Phân tích một vectơ theo 2 vectơ 1 1
không cùng phương c21 0.25
Xác định dấu của các giá trị lượng 1 1
giác c10 0.25
 Trang 2 SP ĐỢT 8, TỔ 5 ĐỀ KIỂM TRA HỌC KÌ I TOÁN 10-2020 
 1 1
 Tính giá trị của biểu thức LG
 c22 0.25
 1 1
 Ứng dụng tích vô hướng tính góc
 c10 0.25
 Xác định tọa độ điểm liên quan đến 1 1
 tích vô hướng c23 0.25
 11 12 4 1 28
 TỔNG CỘNG
 2.75 3 1 0.25 7
  PHẦN TỰ LUẬN: 30%
Câu 1a. Tìm tập xác định của hàm số.
Câu 1b. Xét tính chẵn, lẻ của hàm số
Câu 2. Giải hệ phương trình
Câu 3a. Chứng minh đẳng thức vectơ
Câu 3b. Tính tích vô hướng của hai vectơ
 Trang 3 SP ĐỢT 8, TỔ 5 ĐỀ KIỂM TRA HỌC KÌ I TOÁN 10-2020 
 ĐỀ KIỂM TRA HỌC KÌ I TOÁN 10
 NĂM HỌC 2020-2021
 TỔ 5 THỜI GIAN: 90 PHÚT
 ĐỀ
 A. PHẦN TRẮC NGHIỆM (7,0 điểm)
Câu 1. [Mức độ 1] Cho các tập hợp: A 2;4;6 , B 2;6, C 4;6 , D 4;6;8. Khẳng định nào 
 sau đây đúng? 
 A. A D . B. B  D . C. B C . D. C  D .
Câu 2. [ Mức độ 1] Cho hàm số f x 3 2x . Giá trị của hàm số tại điểm x 1 bằng
 A. 1. B. 3 . C. 5 . D. 5.
Câu 3. [Mức độ 1] Trong các hàm số sau, hàm số nào có đồ thị nhận đường x = 2020 làm trục đối xứng?
 A. y = - 2x 2 + 2020x - 1 . B. y = 2x 2 + 2020x - 5 .
 1
 C. y = x 2 - 2020x - 2 . D. y = x 2 - 2020x + 2 .
 2
 4
Câu 4. [Mức độ 1] Điều kiện xác định của phương trình x 1 là
 x2 1
 A. x  1; .B. x 1; \ 1 . C. x  1; \ 1 . D. x 1;1 .
Câu 5. [Mức độ 1] Trong các phương trình sau, phương trình nào tương đương với phương trình 
 x2 9
 A. x2 3x 4 0 . B. x2 3x 4 0.
 C. x 3. D. x2 x 9 x .
Câu 6. [Mức độ 1] Có bao nhiêu giá trị của tham số m để phương trình m 2 x m2 4 0 vô 
 nghiệm?
 A.0 . B. 1. C. 2 . D. 3.
Câu 7. [Mức độ 1] Cho tam giác có trọng tâm và trung tuyến . Khẳng định nào sau đây là 
 sai?
 A. +2 = 0.B. + + = 3 , ∀ .
 C. .D. .
 = ―2 + + =0  
Câu 8. [Mức độ 1] Cho tam giác ABC đều có độ dài cạnh bằng a . Độ dài AB BC bằng
 3
 A. 2a . B. a 3 . C. a . D. a .
 2
Câu 9. [Mức độ 1] Cho a 1; 5 , b 2; 1 . Tính c 3a 2b .
 A. c 7; 13 . B. c 1; 17 . C. c 1; 17 . D. c 1; 16 .
 Trang 4 SP ĐỢT 8, TỔ 5 ĐỀ KIỂM TRA HỌC KÌ I TOÁN 10-2020 
Câu 10. [Mức độ 1] Cho góc thỏa mãn 900 1800 . Khẳng định nào sau đây là khẳng định đúng? 
 A. cos 0 . B. sin 0 . C. tan 0. D. cot 0 .
     
Câu 11. [ Mức độ 1] Cho OM 2; 1 , ON 3; 1 . Tính góc của OM ,ON 
 2 2
 A. 135o . B. . C. 135o . D. .
 2 2
Câu 12. [Mức độ 2] Cho mệnh đề: “x ¡ , x2 3x 5 0 ”. Mệnh đề phủ định của mệnh đề trên là
 A. x ¡ , x2 3x 5 0 . B. $x Î ¡ ,x2 + 3x + 5 £ 0 .
 C. x ¡ , x2 3x 5 0 .D. x ¡ , x2 3x 5 0.
Câu 13. [Mức độ 2] Cho tập hợp A 1;2;3;4. Hỏi có bao nhiêu tập hợp con của tập hợp A có chứa 
 phần tử 1? 
 A. 1. B. 16 . C. 7 . D. 8 .
  
Câu 14. [Mức độ 2] Cho tam giác ABC vuông tại A , trọng tâm G , AB 6, AC 8 . Độ dài véc-tơ AG
 bằng
 20 10
 A. 10. B. 5 3 .C. .D. .
 3 3
Câu 15. [Mức độ 2] Cho hàm số y 2 2m x m 3 số giá trị m nguyên thuộc đoạn  2021;2021 để 
 hàm số nghịch biến trên ¡ là
 A. 2019 . B. 2020 . C. 2018 . D. 2021.
Câu 16. [Mức độ 2] Cho hai hàm số f x 2x3 3x và g x x2021 3. Mệnh đề nào sau đây đúng?
 A. f x là hàm số lẻ; g x là hàm số lẻ.
 B. f x là hàm số chẵn; g x là hàm số chẵn.
 C. Cả f x và g x đều là hàm số không chẵn, không lẻ.
 D. f x là hàm số lẻ; g x là hàm số không chẵn, không lẻ.
Câu 17. [Mức độ 2] Phương trình x2 2x 3 x 5 có tổng các nghiệm nguyên là 
 A. 2 . B. 3 .C. 1. D. 4 .
Câu 18. [Mức độ 2] Tổng các nghiệm của phương trình 2x 5 5 2x 1 0 là:
 15 15
 A. 5 . B. 0 . C. . D. .
 4 2
 3x 2y 1
Câu 19. [Mức độ 2] Nghiệm của hệ phương trình là 
 2 2x 3y 0
 A. 3; 2 2 B. 3;2 2 
 C. 3;2 2 D. 3; 2 2 
Câu 20. [Mức độ 2] Cho tam giác ABC . Điểm M nằm trên cạnh BC sao cho MB 2MC . Hãy phân 
    
 tích vectơ AM theo hai vectơ u AB , v AC .
  1 2  1 2  1 2  4 2 
 A. AM u v . B. AM u v . C. AM u v .D. AM u v .
 3 3 3 3  3 3 3 3
Câu 21. [Mức độ 2] Trong mặt phẳng Oxy , cho a 2; 1 , b 5;4 và c 3; 2 . Phân tích véc tơ 
 b qua véc tơ a và c ta được:
 A. b 2a 3c B. b 2c 3a C. b 2c 3a D. b 3c 2a
 Trang 5 SP ĐỢT 8, TỔ 5 ĐỀ KIỂM TRA HỌC KÌ I TOÁN 10-2020 
 2 3sin 2cos 
Câu 22. [Mức độ 2] Cho biết tan . Giá trị của biểu thức E bằng
 3 5sin cos 
 19 25 12
 A. . B. 1. C. . D. .
 13 13 7
Câu 23. [Mức độ 2] Trong mặt phẳng tọa độ Oxy , cho A 1;2 , B 2;6 , C 9;8 . Gọi H a;b là hình 
 chiếu của A lên cạnh BC . Khi đó b 2a bằng
 A. 6 . B. 13 . C. 13. D. 6 .
Câu 24. [Mức độ 3] Biết rằng hàm số y ax2 bx c a 0 đạt giá trị nhỏ nhất bằng 4 tại x 2 và 
 có đồ thị hàm số đi qua điểm A 0;6 . Tính tích P abc. 
 3
 A. P 6 . B. P 6 . C. P 3 . D. P .
 2
Câu 25. [Mức độ 3] Giá trị lớn nhất và giá trị nhỏ nhất của hàm số y x4 4x2 3 trên  1;2 là a và 
 b . Khi đó P a b bằng
 A. 7 . B. 4 . C. 10 . D. 10 .
Câu 26. [Mức độ 3] Tìm tất cả các giá trị của tham số m để đường thẳng : y 2x m cắt 
 P : y x2 4x 1 tại hai điểm phân biệt có hoành độ dương. 
 A. 8 m 1. B. m 8 . C. m 1. D. 8 m 1.
Câu 27. [Mức độ 3] Cho hình thang ABCD AB//CD , có CD 2AB , H là trung điểm của cạnh DC , 
     
 M là điểm thỏa mãn đẳng thức MH AD MH HD . Khẳng định nào sau đây là đúng?
 A. Quỹ tích điểm M là đường trung trực của đoạn thẳng BC ..
 B. Quỹ tích điểm M là đường trung trực của đoạn thẳng HD ..
 C. Quỹ tích điểm M là đường trung trực của đoạn thẳng AB .
 D. Quỹ tích điểm M là đường trung trực của đoạn thẳng BD .
Câu 28. [Mức độ 4] Có bao nhiêu số nguyên m thuộc nửa khoảng  2020 ; 2020 để phương trình 
 2x2 3x 4m x 3 có nghiệm.
 A. 2017 . B. 2018 . C. 2019 . D. 2020 .
 B. PHẦN TỰ LUẬN (3,0 điểm)
 x 3
Câu 1a. [Mức độ 1] Tìm tập xác định của hàm số f x .
 x 2
Câu 1b. [Mức độ 2] Xét tính chẵn, lẻ của hàm số f x 2020 x 2020 x .
 mx y 3
Câu 2. [Mức độ 2] Cho hệ phương trình 
 2x 2y 9
 a) Giải hệ phương trình khi m 2 .
 b) Tìm m để hệ có nghiệm duy nhất x0; y0 thỏa mãn điều kiện x0 2y0 4 .
Câu 3a. [Mức độ 2] Cho tam giác ABC, gọi M là trung điểm của BC và I là trung điểm của AM. Chứng 
    
 minh rằng: 2IA IB IC 0 . 
Câu 3b. [Mức độ 3] Cho hình thang cân ABCD biết đáy lớn CD 3a , AB a và BC a 2 . Gọi H là hình 
    
 chiếu vuông góc của A lên cạnh CD . Tính BH. AC AD .
  HẾT 
 Trang 6 SP ĐỢT 8, TỔ 5 ĐỀ KIỂM TRA HỌC KÌ I TOÁN 10-2020 
 LỜI GIẢI CHI TIẾT
 BẢNG ĐÁP ÁN CÁC CÂU TRẮC NGHIỆM
 1D 2C 3D 4B 5C 6A 7C 8D 9C 10A 11A 12B 13D 14D
 15D 16D 17B 18D 19D 20B 21A 22D 23D 24A 25D 26D 27A 28A
 A. PHẦN TRẮC NGHIỆM (7,0 điểm)
Câu 1. [Mức độ 1] Cho các tập hợp: A 2;4;6 , B 2;6, C 4;6 , D 4;6;8. Khẳng định nào 
 sau đây đúng? 
 A. A D . B. B  D . C. B C . D. C  D .
 Lời giải
 FB tác giả: Dũng Đào
 Ta có: 
 + 2 A 2;4;6 và 2 D 4;6;8 nên A D . Đáp án A sai.
 + 2 B 2;6 và 2 D 4;6;8 nên B  D . Đáp án B sai.
 + 2 B 2;6 và 2 C 4;6 nên B C . Đáp án C sai.
 + 4;6 C 4;6 và 4;6 D 4;6;8 nên C  D . Đáp án D đúng.
Câu 2. [ Mức độ 1] Cho hàm số f x 3 2x . Giá trị của hàm số tại điểm x 1 bằng
 A. 1. B. 3 . C. 5 . D. 5.
 Lời giải
 FB tác giả: Dung Nguyễn 
 Thay x 1 vào hàm số f x 3 2x , ta được f 1 3 2 1 5
 Vậy giá trị của hàm số tại điểm x 1 bằng 5 .
Câu 3. [Mức độ 1] Trong các hàm số sau, hàm số nào có đồ thị nhận đường x = 2020 làm trục đối xứng?
 A. y = - 2x 2 + 2020x - 1 . B. y = 2x 2 + 2020x - 5 .
 1
 C. y = x 2 - 2020x - 2 . D. y = x 2 - 2020x + 2 .
 2
 Lời giải
 FB tác giả: Duong Quynh Nga
 b
 Trục đối xứng của parabol y = ax 2 + bx + c (a ¹ 0) có phương trình x = - . 
 2a
 Áp dụng vào các đáp án, chọn D. 
 4
Câu 4. [Mức độ 1] Điều kiện xác định của phương trình x 1 là
 x2 1
 A. x  1; .B. x 1; \ 1 . C. x  1; \ 1 . D. x 1;1 .
 Lời giải
 FB tác giả: Good Hope
 Trang 7 SP ĐỢT 8, TỔ 5 ĐỀ KIỂM TRA HỌC KÌ I TOÁN 10-2020 
 x2 1 0 x 1 x 1
 Đk .
 x 1 0 x 1 x 1
 x 1; \ 1 .
Câu 5. [Mức độ 1] Trong các phương trình sau, phương trình nào tương đương với phương trình 
 x2 9
 A. x2 3x 4 0 . B. x2 3x 4 0.
 C. x 3. D. x2 x 9 x .
 Lời giải
 FB tác giả: Hằng-Ruby-Nguyễn
 • x2 9 x 3.
 • x 3 x 3.
 Hai phương trình này có cùng tập nghiệm nên chúng tương đương. Suy ra đáp án C.
Câu 6. [Mức độ 1] Có bao nhiêu giá trị của tham số m để phương trình m 2 x m2 4 0 vô 
 nghiệm?
 A.0 . B. 1. C. 2 . D. 3.
 Lời giải
 FB tác giả: Hoàng Hạnh
 m 2 0 m 2
 Phương trình 2 vô nghiệm khi
 m 2 x m 4 0 2 m 
 m 4 0 m 2
 Không có giá trị nào của tham số m để phương trình vô nghiệm.
Câu 7. [Mức độ 1] Cho tam giác có trọng tâm và trung tuyến . Khẳng định nào sau đây là 
 sai?
 A. +2 = 0.B. + + = 3 , ∀ .
 C. = ―2 .D. + + = 0.
 Lời giải
 FB tác giả: Hồ Bình Minh
 A
 G
 C
 B M
 A đúng vì = ―2 ⇒ +2 = 0.
 B đúng theo tính chất trọng tâm.
 C sai vì = ―3 .
 D đúng theo tính chất trọng tâm. Suy ra: Đáp án C.   
Câu 8. [Mức độ 1] Cho tam giác ABC đều có độ dài cạnh bằng a . Độ dài AB BC bằng
 Trang 8 SP ĐỢT 8, TỔ 5 ĐỀ KIỂM TRA HỌC KÌ I TOÁN 10-2020 
 3
 A. 2a . B. a 3 . C. a . D. a .
 2
 Lời giải
 FB tác giả: Ho Ngoc Hung
    
 Ta có: AB BC AC AC a .
Câu 9. [Mức độ 1] Cho a 1; 5 , b 2; 1 . Tính c 3a 2b .
 A. c 7; 13 . B. c 1; 17 . C. c 1; 17 . D. c 1; 16 .
 Lời giải
 FB tác giả: Huonglee
 3a (3;15)
 Ta có: 
 2b ( 4;2)
 Do đó c 3a 2b ( 1;17) .
Câu 10. [Mức độ 1] Cho góc thỏa mãn 900 1800 . Khẳng định nào sau đây là khẳng định đúng? 
 A. cos 0 . B. sin 0 . C. tan 0. D. cot 0 .
 Lời giải
 FB tác giả: Huy Nguyen
 Ta có 900 1800 sin 0, cos 0, tan 0, cot 0 .
 Do đó đáp án đúng là A .
     
Câu 11. [ Mức độ 1] Cho OM 2; 1 , ON 3; 1 . Tính góc của OM ,ON 
 2 2
 A. 135o . B. . C. 135o . D. .
 2 2
 Lời giải
 FB tác giả : Đỗ Mạnh Hà
   
   OM.ON 5 2   
 Ta có cos OM ,ON   OM ,ON 135o .
 OM .ON 5. 10 2
Câu 12. [Mức độ 2] Cho mệnh đề: “x ¡ , x2 3x 5 0 ”. Mệnh đề phủ định của mệnh đề trên là
 A. x ¡ , x2 3x 5 0 . B. $x Î ¡ ,x2 + 3x + 5 £ 0 .
 C. x ¡ , x2 3x 5 0 .D. x ¡ , x2 3x 5 0.
 Lời giải
 FB tác giả : Lê Chung
Câu 13. [Mức độ 2] Cho tập hợp A 1;2;3;4. Hỏi có bao nhiêu tập hợp con của tập hợp A có chứa 
 phần tử 1? 
 Trang 9 SP ĐỢT 8, TỔ 5 ĐỀ KIỂM TRA HỌC KÌ I TOÁN 10-2020 
 A. 1. B. 16 . C. 7 . D. 8 .
 Lời giải
 FB tác giả: Lê Hồng Phi
 Các tập hợp con của tập hợp A có chứa phần tử 1 là
 1 , 1;2, 1;3 , 1;4, 1;2;3 , 1;2;4 , 1;3;4 , 1;2;3;4.
 Vậy có tất cả 8 tập hợp con của tập hợp A có chứa phần tử 1.
  
Câu 14. [Mức độ 2] Cho tam giác ABC vuông tại A , trọng tâm G , AB 6, AC 8 . Độ dài véc-tơ AG
 bằng
 20 10
 A. 10. B. 5 3 .C. . D. .
 3 3
 Lời giải
 Tác giả: Lê Văn Lương ; Fb: Lê Lương
 Tam giác ABC vuông tại A nên BC AB2 AC 2 10
 BC
 Gọi M là trung điểm của BC AM 5
 2
 2 10
 G là trọng tâm tam giác nên AG AM 
 3 3
  10
 Vậy AG AG 
 3
Câu 15. [Mức độ 2] Cho hàm số y 2 2m x m 3 số giá trị m nguyên thuộc đoạn  2021;2021 để 
 hàm số nghịch biến trên ¡ là
 A. 2019 . B. 2020 . C. 2018 . D. 2021.
 Lời giải
 FB tác giả: Lê Văn Hùng
 Hàm số nghịch biến trên ¡ 2 2m 0 m 1
 Vậy số giá trị nguyên của m  2021;2021 là 2;3;4;...;2021
 Do đó số giá trị nguyên là 2020 giá trị
Câu 16. [Mức độ 2] Cho hai hàm số f x 2x3 3x và g x x2021 3. Mệnh đề nào sau đây đúng?
 A. f x là hàm số lẻ; g x là hàm số lẻ.
 B. f x là hàm số chẵn; g x là hàm số chẵn.
 C. Cả f x và g x đều là hàm số không chẵn, không lẻ.
 D. f x là hàm số lẻ; g x là hàm số không chẵn, không lẻ.
 Lời giải
 FB tác giả: Lê Văn Quyết
 • Xét f x 2x3 3x có TXĐ: D ¡ nên x D x D.
 Ta có f x 2 x 3 3 x 2x3 3x f x  f x là hàm số lẻ.
 • Xét g x x2021 3 có TXĐ: D ¡ nên x D, x D.
 Trang 10