Đề kiểm tra 45 phút môn Đại số Lớp 10 - Tổ 1 - Chủ đề: Hàm số (Số 2) - Năm học 2020-2021 (Có đáp án)

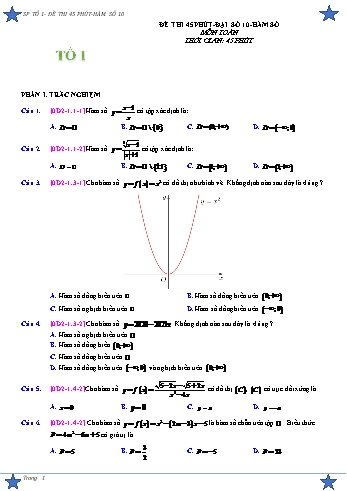
 SP TỔ 1- ĐỀ THI 45 PHÚT-HÀM SỐ 10 
 ĐỀ THI 45 PHÚT-ĐẠI SỐ 10-HÀM SỐ
 MÔN TOÁN
 THỜI GIAN: 45 PHÚT
 TỔ 1
PHẦN I. TRẮC NGHIỆM
 x 1
Câu 1. [0D2-1.1-1] Hàm số y có tập xác định là:
 x
 A. D ¡ . B. D ¡ \ 0 . C. D (0; ) . D. D ;0 .
 3 x 1
Câu 2. [0D2-1.1-2] Hàm số y có tập xác định là:
 x 1
 A. D ¡ . B. D ¡ \ 1 . C. D 1; . D. D 1; .
Câu 3. [0D2-1.3-1] Cho hàm số y f x x2 có đồ thị như hình vẽ. Khẳng định nào sau đây là đúng ?
 A. Hàm số đồng biến trên ¡ . B. Hàm số đồng biến trên 0; .
 C. Hàm số nghịch biến trên ¡ . D. Hàm số đồng biến trên ;0 .
Câu 4. [0D2-1.3-2] Cho hàm số y 2020 2021x . Khẳng định nào sau đây là đúng ? 
 A. Hàm số nghịch biến trên ¡ .
 B. Hàm số đồng biến 0; .
 C. Hàm số đồng biến trên ¡ .
 D. Hàm số đồng biến trên ;0 và nghịch biến trên 0; .
 5 2x 5 2x
Câu 5. [0D2-1.4-2] Cho hàm số y f x có đồ thị C , C có trục đối xứng là 
 x3 4x
 A. x 0 . B. y 0. C. y x . D. y x .
Câu 6. [0D2-1.4-2] Cho hàm số y f x x2 2m 3 x 5 là hàm số chẵn trên tập ¡ . Biểu thức 
 P 4m2 6m 5 có giá trị là
 3
 A. P 5. B. P . C. P 5 . D. P 23.
 2
 Trang 1 SP TỔ 1- ĐỀ THI 45 PHÚT-HÀM SỐ 10 
Câu 7. [0D2-2.4-2] Cho hàm số y f x 2 3m x 3 , có đồ thị d và thỏa mãn
 f x 0,x  1;2 , thì m lấy giá trị thuộc khoảng nào?
 A. m 0;1 . B. m 1;1 . C. m 0;2 . D. m 1;2 .
Câu 8. [0D2-2.4-3] Cho hàm số y f x m 2 x 7 , có đồ thị d và thỏa mãn f x 0,x  3;1 
 thì biểu thức Q m2 2m 7 có giá trị nhỏ nhất thuộc khoảng nào?
 A. 10, 9 . B. 9; 8 . C. 8; 7 . D. 7; 6 .
Câu 9. [0D2-3.1-1] Tọa độ đỉnh của parabol P : y x2 2x 2 là
 A. 1;1 . B. 1; 3 . C. 2;6 . D. 2; 2 .
Câu 10. [0D2-3.3-2] Đồ thị của hàm số nào có dạng như đường cong trong hình vẽ dưới đây?
 A. y x 2 . B. y x2 2x 2.
 C. y x2 2x 2 . D. y x2 2x 2 .
Câu 11. [0D2-3.2-3] Cho hàm số f x ax2 bx c a 0 . Biết đồ thị là một đường parabol có đỉnh 
 I 1; 3 và cắt trục tung tại điểm có tung độ bằng 1. Giá trị của f 3 bằng
 A. 9. B. 21. C. 1. D. 5.
Câu 12. [0D2-3.4-1] Cho parabol P : y 9x2 3x 2 . Đường thẳng d : y 3x 1. Số giao điểm của 
 P với đường thẳng d là 
 A. 0. B. 1. C. 2. D. 3.
Câu 13. [0D2-3.4-2] Có bao nhiêu giá trị nguyên của m  10;10 để parabol P : 
 2
 y x 2 m 1 x m 2 cắt trục Ox tại hai điểm phân biệt nằm về hai phía đối với trục tung?
 A. 10.B. 11. C. 12. D. 13.
 2 
Câu 14. [0D2-3.4-3] Tất cả các giá trị của m để parabol P : y x 2mx 2m cắt đường thẳng 
 d : y 2x 3 tại hai điểm phân biệt có hoành độ nhỏ hơn 2 là
 m 2 1
 1 m 
 A. m 2 .B. m .C. 1 .D. 2 .
 2 m 
 2 m 2
Câu 15. [0D2-3.1-3] Cho phương trình x2 2 m 3 x m2 3 0 , m là tham số. Tìm m để phương trình 
 có hai nghiệm x1, x2 và P 5(x1 x2 ) 2x1x2 đạt giá trị lớn nhất.
 5 5
 A. m .B. m .C. m 2 .D. m 2 .
 2 2
 Trang 2 SP TỔ 1- ĐỀ THI 45 PHÚT-HÀM SỐ 10 
PHẦN II. TỰ LUẬN
Câu 1. [0D2-3.2-2] Xác định parabol P : y ax2 bx 2 , a 0 biết P đi qua B 3; 4 và có trục 
 3
 đối xứng là x .
 2
Câu 2. [0D2-3.4-3] Cho parabol P : y x2 m 1 x m . Tìm tất cả giá trị của tham số m đề P cắt 
 trục hoành tại hai điểm phân biệt A, B sao cho tam giác IAB có diện tích bằng 1, trong đó I là 
 đỉnh của P . 
Câu 3. [0D2-3.2-4] Cho hàm số y f x có đồ thị đi qua điểm M 1;2 . Biết rằng đồ thị hàm số 
 g x f 2 x 2 f x là một parabol có đỉnh là I 2;7 . Tính f 2 .
 BẢNG ĐÁP ÁN TRẮC NGHIỆM
 1.B 2.A 3.B 4.A 5.A 6.A 7.D 8.C 9.B 10.D
 11.D 12.B 13.C 14.C 15.D
 LỜI GIẢI CHI TIẾT
 x 1
Câu 1. [0D2-1.1-1] Hàm số y có tập xác định là:
 x
 A. D ¡ . B. D ¡ \ 0 . C. D (0; ) . D. D ;0 .
 Lời giải
 FB tác giả: Thanh Tâm Trần 
 Hàm số xác định khi và chỉ khi x 0 . 
 Vậy tập xác định của hàm số là: D ¡ \ 0 . 
 3 x 1
Câu 2. [0D2-1.1-2] Hàm số y có tập xác định là:
 x 1
 A. D ¡ . B. D ¡ \ 1 . C. D 1; . D. D 1; .
 Lời giải
 FB tác giả: Thanh Tâm Trần 
 Hàm số xác định khi và chỉ khi x 1 0 ( luôn đúng vì x 1 1,x ¡ ).
 Vậy tập xác định của hàm số là D ¡ .
Câu 3. [0D2-1.3-1] Cho hàm số y f x x2 có đồ thị như hình vẽ. Khẳng định nào sau đây là đúng ?
 Trang 3 SP TỔ 1- ĐỀ THI 45 PHÚT-HÀM SỐ 10 
 A. Hàm số đồng biến trên ¡ . B. Hàm số đồng biến trên 0; .
 C. Hàm số nghịch biến trên ¡ . D. Hàm số đồng biến trên ;0 .
 Lời giải
 FB tác giả: Trần Thanh Tâm 
 Từ đồ thị hàm số suy ra hàm số đồng biến trên 0; và nghịch biến trên ;0 . 
Câu 4. [0D2-1.3-2] Cho hàm số y 2020 2021x . Khẳng định nào sau đây là đúng ? 
 A. Hàm số nghịch biến trên ¡ .
 B. Hàm số đồng biến 0; .
 C. Hàm số đồng biến trên ¡ .
 D. Hàm số đồng biến trên ;0 và nghịch biến trên 0; .
 Lời giải
 FB tác giả: Trần Thanh Tâm 
 Ta có y 2020 2021x 2021x 2020 là hàm số bậc nhất và có hệ số a 2021 0 nên hàm số 
 nghịch biến trên ¡ .
 5 2x 5 2x
Câu 5. [0D2-1.4-2] Cho hàm số y f x có đồ thị C , C có trục đối xứng là 
 x3 4x
 A. x 0 . B. y 0. C. y x . D. y x .
 Lời giải
 FB tác giả: Nguyễn Trí Chính. 
 5 2x 0 5 5
 x 
 Điều kiện xác định: 5 2x 0 2 2
 3 x 0; x 2
 x 4x 0 
 5 5 
 Tập xác định D ; \ 2;0;2 .
 2 2 
 5 2x 5 2x
 Có x D thì x D , f x f x , x D .
 x3 4x
 y f x là hàm số chẵn, nên đồ thị C nhận trục Oy :x 0 làm trục đối xứng.
Câu 6. [0D2-1.4-2] Cho hàm số y f x x2 2m 3 x 5 là hàm số chẵn trên tập ¡ . Biểu thức 
 P 4m2 6m 5 có giá trị là
 Trang 4 SP TỔ 1- ĐỀ THI 45 PHÚT-HÀM SỐ 10 
 3
 A. P 5. B. P . C. P 5 . D. P 23.
 2
 Lời giải
 FB tác giả: Nguyễn Trí Chính.
 Ta có y f x x2 2m 3 x 5 là hàm số chẵn trên ¡
 f x f x ,x ¡
 x2 2m 3 x 5 x2 2m 3 x 5 , x ¡ .
 3
 2 2m 3 x 0,x ¡ m .
 2
 3
 Với m , ta có P 4m2 6m 5 5 .
 2
Câu 7. [0D2-2.4-2] Cho hàm số y f x 2 3m x 3 , có đồ thị d và thỏa mãn
 f x 0,x  1;2 , thì m lấy giá trị thuộc khoảng nào?
 A. m 0;1 . B. m 1;1 . C. m 0;2 . D. m 1;2 .
 Lời giải
 FB tác giả: Nguyễn Trí Chính.
 Xét y f x 2 3m x 3 , f x 0,x  1;2
 f 1 0 1 3m 0 1 7
 m .
 f 2 0 7 6m 0 3 6
Câu 8. [0D2-2.4-3] Cho hàm số y f x m 2 x 7 , có đồ thị d và thỏa mãn f x 0,x  3;1 
 thì biểu thức Q m2 2m 7 có giá trị nhỏ nhất thuộc khoảng nào?
 A. 10, 9 . B. 9; 8 . C. 8; 7 . D. 7; 6 .
 Lời giải
 FB tác giả: Nguyễn Trí Chính. 
 Xét hàm số y f x m 2 x 7 , f x 0,x  3;1.
 f 3 0 3m 1 0 1
 m 9 .
 f 1 0 m 9 0 3
 2
 2 2 1 1 4 4 68 1 4 1 68
 Xét hàm số g m m 2m 7 m 2. m m m m 
 3 9 3 9 9 3 3 3 9
 1 1
 Có m 9 0 m .
 3 3
 68 1
 Suy ra g m . Đẳng thức xảy ra khi m (thỏa mãn điều kiện).
 9 3
 68 1
 Vậy min Q 7,6 , đạt được khi m .
 1 
 ;9 9 3
 3 
 Trang 5 SP TỔ 1- ĐỀ THI 45 PHÚT-HÀM SỐ 10 
Câu 9. [0D2-3.1-1] Tọa độ đỉnh của parabol P : y x2 2x 2 là
 A. 1;1 . B. 1; 3 . C. 2;6 . D. 2; 2 .
 Lời giải
 FB tác giả: Giáp Minh Đức 
 2 b 
 Hàm số bậc hai y ax bx c có đồ thị là parabol, có tọa độ đỉnh là ; .
 2a 4a 
 Vậy tọa độ đỉnh của parabol P đã cho là 1; 3 .
Câu 10. [0D2-3.3-2] Đồ thị của hàm số nào có dạng như đường cong trong hình vẽ dưới đây?
 A. y x 2 . B. y x2 2x 2.
 C. y x2 2x 2 . D. y x2 2x 2 .
 Lời giải
 FB tác giả: Giáp Minh Đức 
 Đồ thị hàm số là đường cong parabol nên đáp án A loại.
 Đồ thị là đường cong parabol có bề lõm quay xuống dưới nên hệ số của x2 phải âm suy ra loại đáp 
 án C.
 Đồ thị cắt trục tung tại điểm của tung độ dương suy ra loại đáp án B. 
 Đáp án đúng là đáp án D.
 Cách 2: (ngắn gọn)
 Đồ thị là đường cong parabol có bề lõm quay xuống dưới và cắt trục tung tại điểm có tung độ dương 
 suy ra đáp án D là đáp án đúng.
Câu 11. [0D2-3.2-3] Cho hàm số f x ax2 bx c a 0 . Biết đồ thị là một đường parabol có đỉnh 
 I 1; 3 và cắt trục tung tại điểm có tung độ bằng 1. Giá trị của f 3 bằng
 A. 9. B. 21. C. 1. D. 5.
 Lời giải
 FB tác giả: Giáp Minh Đức 
 b
 1
 2a 2a b 0 2a b 0 a 2
 Từ giả thiết ta có f 1 3 a b c 3 a b 2 b 4 .
 c 1 c 1 c 1
 f 0 1 
 Suy ra hàm số đã cho là f x 2x2 4x 1. Vậy f 3 5.
Câu 12. [0D2-3.4-1] Cho parabol P : y 9x2 3x 2 . Đường thẳng d : y 3x 1. Số giao điểm của 
 P với đường thẳng d là 
 Trang 6 SP TỔ 1- ĐỀ THI 45 PHÚT-HÀM SỐ 10 
 A. 0. B. 1. C. 2. D. 3.
 Lời giải
 FB tác giả: Nguyễn Bình 
 Phương trình hoành độ giao điểm của d với P là:
 1
 9x2 3x 2 3x 1 9x2 6x 1 0 x .
 3
 Vậy số giao điểm của P với đường thẳng d là 1. 
Câu 13. [0D2-3.4-2] Có bao nhiêu giá trị nguyên của m  10;10 để parabol P : 
 2
 y x 2 m 1 x m 2 cắt trục Ox tại hai điểm phân biệt nằm về hai phía đối với trục tung?
 A. 10.B. 11. C. 12. D. 13.
 Lời giải
 FB tác giả: Nguyễn Bình 
 Phương trình hoành độ giao điểm của P với Ox là:
 x2 2 m 1 x m 2 0 1 .
 P cắt trục Ox tại hai điểm phân biệt nằm về hai phía đối với trục tung khi và chỉ khi phương 
 trình 1 có hai nghiệm trái dấu m 2 0 m 2.
 Vì m nguyên thuộc đoạn  10;10 nên m 10; 9;....;0;1 .
 Suy ra có 12 giá trị của m thỏa mãn yêu cầu bài toán. Chọn đáp án C.
Câu 14. [0D2-3.4-3] Tất cả các giá trị của m để parabol P : y x2 2mx 2m cắt đường thẳng 
 d : y 2x 3 tại hai điểm phân biệt có hoành độ nhỏ hơn 2 là
 m 2 1
 1 m 
 A. m 2 .B. m .C. 1 .D. 2 .
 2 m 
 2 m 2
 Lời giải
 FB tác giả: Nguyễn Bình 
 Phương trình hoành độ giao điểm của d với P là:
 2 x 1
 x 2mx 2m 2x 3 x 1 x 3 2m 0 .
 x 3 2m
 P cắt đường thẳng d tại hai điểm phân biệt có hoành độ nhỏ hơn 2
 m 2
 3 2m 1 
 1 .
 3 2m 2 m 
 2
Câu 15. [0D2-3.1-3] Cho phương trình x2 2 m 3 x m2 3 0 , m là tham số. Tìm m để phương trình 
 có hai nghiệm x1, x2 và P 5(x1 x2 ) 2x1x2 đạt giá trị lớn nhất.
 5 5
 A. m .B. m .C. m 2 .D. m 2 .
 2 2
 Lời giải
 FB tác giả: Phạm Thúy
 Trang 7 SP TỔ 1- ĐỀ THI 45 PHÚT-HÀM SỐ 10 
 Ta có ' m 3 2 m2 3 6m 12 .
 Phương trình có nghiệm ' 0 6m 12 0 m 2 .
 x1 x2 2 m 3 
 Theo định lý Viét ta có 2 .
 x1x2 m 3
 P 10 m 3 2 m2 3 2m2 10m 24 .
 Xét hàm số y 2m2 10m 24 với m  2; .
 Bảng biến thiên 
 Suy ra max y 12 khi và chỉ khi m 2 . Vậy m 2 là giá trị cần tìm.
  2; 
PHẦN II. TỰ LUẬN
Câu 1. [0D2-3.2-2] Xác định parabol P : y ax2 bx 2 , a 0 biết P đi qua B 3; 4 và có trục 
 3
 đối xứng là x .
 2
 Lời giải
 FB tác giả: Phạm Thúy
 Ta có P đi qua B 3; 4 nên 4 9a 3b 2 3a b 2 1 .
 3 b 3
 P có trục đối xứng là x nên b 3a . Thay b 3a vào 1 ta được:
 2 2a 2
 1
 3a 3a 2 a b 1 .
 3
 1
 Vậy P cần tìm là y x2 x 2 .
 3
Câu 2. [0D2-3.4-3] Cho parabol P : y x2 m 1 x m . Tìm tất cả giá trị của tham số m đề P cắt 
 trục hoành tại hai điểm phân biệt A, B sao cho tam giác IAB có diện tích bằng 1, trong đó I là 
 đỉnh của P . 
 Lời giải
 FB tác giả: thuy.luu.33886
 2
 Phương trình hoành độ giao điểm của P với trục hoành là: x m 1 x m 0 | 1 .
 P cắt trục hoành tại hai điểm phân biệt khi và chỉ khi phương trình 1 có hai nghiệm phân biệt, 
 hay 0 m 1 2 4m 0 m 1 2 0 m 1 .
 Trang 8 SP TỔ 1- ĐỀ THI 45 PHÚT-HÀM SỐ 10 
 Gọi x1 , x2 là hai nghiệm của phương trình 1 , ta có x1 1; x2 m .
 Suy ra AB x1 x2 m 1 .
 2
 m 1 m 1 
 Tọa độ đỉnh I ; .
 2 4 
 2
 1 1 m 1 
 Ta có S 1 AB.d I, AB 1 m 1 1
 IAB 2 2 4
 3 m 1
 m 1 8 m 1 2 (thỏa mãn ).
 m 3
 Vậy giá trị m cần tìm là m 3;1 .
Câu 3. [0D2-3.2-4] Cho hàm số y f x có đồ thị đi qua điểm M 1;2 . Biết rằng đồ thị hàm số 
 g x f 2 x 2 f x là một parabol có đỉnh là I 2;7 . Tính f 2 .
 Lời giải
 FB tác giả: Luan Vu 
 Cách 1: 
 Giả sử g x ax2 bx c a 0 .
 b
 2 b 4a
 Vì I 2;7 là đỉnh của parabol y g x nên ta có 2a 1 .
 4a 2b c 7
 g 2 7
 Mặt khác đồ thị hàm số y f x đi qua M 1;2 nên f 1 2
 g 1 f 2 1 2 f 1 f 1 2 a b c 2 2 .
 b 4a b 4a a 1
 Từ 1 và 2 ta có hệ 4a 2b c 7 4a c 7 b 4 .
 a b c 2 5a c 2 c 3
 Khi đó ta có: f 2 x 2 f x x2 4x 3,x ¡ * .
 2
 Thay x bởi 2 x trong * ta được f x 2 f 2 x 2 x 4 2 x 3,x ¡ hay 
 1 1
 f x f 2 x x2 8x 9 ,x ¡ ** .
 2 2 
 3 3 3
 Cộng vế với vế các đẳng thức * và ** ta được f x x2 ,x ¡ .
 2 2 2
 f x x2 1,x ¡ .
 Vậy f 2 3.
 Cách 2: Tai Van Pham
 Vì g x là parabol có đỉnh là I 2;7 nên g x k x 2 2 7 .
 Trang 9 SP TỔ 1- ĐỀ THI 45 PHÚT-HÀM SỐ 10 
 Ta có: g 1 f 1 2 f 1 f 1 2 nên k 1 2 2 7 2 k 1.
 Suy ra g x x2 4x 3.
 Vì f x và f 2 x cùng bậc nên f x ax2 bx c .
 f 2 x 2 f x x2 4x 3,x ¡
 2
 a 2 x b 2 x c 2 ax2 bx c x2 4x 3,x ¡
 ax2 4a 3b x 4a 2b c x2 4x 3,x ¡
 a 1 a 1
 4a 3b 4 b 0 .
 4a 2b c 3 c 1
 Suy ra f x x2 1.
 2
 Vậy f 2 2 1 3 .
Trang 10